田元生

(湘南學院數(shù)學系,湖南郴州 423000)

帶p-Laplacian算子三點邊值問題擬對稱正解的多重性

田元生

(湘南學院數(shù)學系,湖南郴州 423000)

應(yīng)用Avery-Peterson不動點定理,討論了一類帶p-Laplacian算子三點邊值問題在非線性項f依賴于未知函數(shù)的一階導(dǎo)數(shù)的情況下擬對稱正解的多重性,得到了這類邊值問題至少存在三個擬對稱正解的充分條件.

p-Laplacian算子;三點邊值問題;擬對稱正解;錐

1 引言

帶p-Laplacian算子微分方程的邊值問題,在非牛頓力學,宇宙物理,血漿問題和彈性理論等諸多領(lǐng)域都有廣泛的應(yīng)用.人們對此類邊值問題正解的存在性進行了深入的研究,取得很多有意義的成果[14].最近幾年,對邊值問題的對稱正解和擬對稱正解的存在性及多重性的關(guān)注逐漸增多.文[5]通過建立一個線性算子,利用線性算子的譜理論,研究了一類邊值問題的對稱正解的存在性和多重性.文[6]給出了擬對稱函數(shù)的定義,應(yīng)用五個泛函的不動點定理研究了下面邊值問題擬對稱正解的存在性.本文應(yīng)用Avery-Peterson不動點定理,把文[7]中得到擬對稱正解的存在性和多重性結(jié)論,推廣到帶p-Lpalcian算子的邊值問題(Q)上.

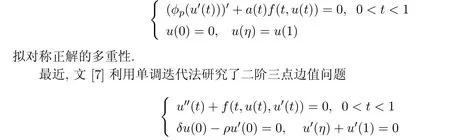
在本文中,總假定以下條件成立

2 預(yù)備知識

為了證明本文的主要結(jié)果,需要如下的預(yù)備知識.

定義2.1設(shè)E是一個實Banach空間,如果P是E中某非空凸閉子集,并且滿足下面兩個條件:

定義2.2設(shè)η∈(0,1),稱函數(shù)u∈C1[0,1]關(guān)于η是擬對稱的,如果

定義2.3映射α稱為P上的非負連續(xù)凹泛函,只要α:P?→[0,∞)連續(xù)且

對所有的x,y∈P以及0≤t≤1成立.類似地,稱映射γ是P上的非負連續(xù)凸泛函,只要γ:P?→[0,∞)連續(xù)且

對所有的x,y∈P以及0≤t≤1成立.

定義2.4給定正數(shù)a,b,c,和d,設(shè)γ和θ是P上的非負連續(xù)凸泛函,α是P上的非負連續(xù)凹函數(shù),ψ是P上的非負連續(xù)泛函.定義凸集

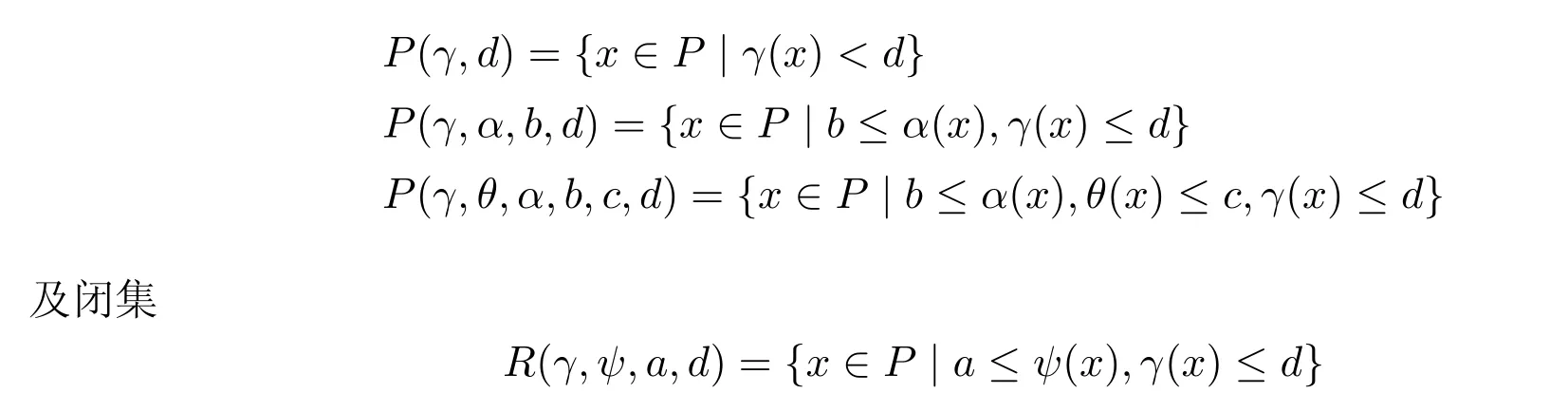
本文主要結(jié)論的證明要用下面的Avery-Peterson不動點定理.

定理2.1[8]令P是實Banach空間E中的錐,設(shè)γ和θ是P上的非負連續(xù)凸泛函,α 是P上的非負連續(xù)凹泛函,ψ是P上的非負連續(xù)泛函且滿足ψ(λx)≤λψ(x),0≤λ≤1,存在正數(shù)M和d,使得

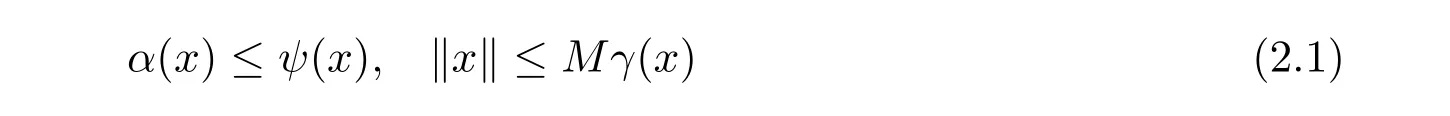
3 主要結(jié)論及其證明

于是,根據(jù)A rzela-Ascoli定理知T(D)為列緊集.其次由勒貝格控制收斂定理不難證明T在P上是連續(xù)的.因此T:P?→P是全連續(xù)的.

為了方便,引用下面記號由條件(A1)知:f(t,u,v)≤φp(d/H).另一方面,對u∈P,有Tu∈P,則Tu在[0,1]上凹,于是

[1]Su H,Wei Z L,Wang B H.The existence of positive solutions for a nonlinear four-point singu lar boundary value prob lem with a p-Laplacian operator[J].Nonlinear Anal.,2007,66:2204-2217.

[2]Jin J X,Y in C H.Positive solutions for the boundary value problems of one-dim ensional p-Laplacian with delay[J].J.Math.Anal.App l.,2007,330:1238-1248.

[3]Sun B,Ge W G,Zhao D X.Three positive solutions for multipoint one-dimensional p-Laplacian boundary value prob lem swith dependence on the first order derivative[J].M ath.Com p.Mode.,2007,45:1170-1178.

[4]M a D X,Han J X,Chen X G.Positive solution of boundary value p roblem for one-dim ensinal p-Laplacian with singu larities[J].J.Math.Anal.App l.,2006,324:118-133.

[5]Sun Y P.Optim alexistence criteria for symm etric positive solutions a three-point boundary value p roblem[J]. Nonlinear Anal.,2007,66:1051-1063.

[6]Avery R I.Henderson J.Existence of three positive pseudo-symm etric solutions for a one-dim ensional p-Laplacian[J].J.M ath.Anal.App l.,2003,277:395-404.

[7]Pang H H,Feng M Q,Ge W G.Existence and m onotone iteration of position solutions for a three-point boundary value problem[J].App l.M ath.Letters,2008,21:656-661.

[8]Avery R I,Peterson A C.Three positive fixed points of nonlinear operators on orderd Banach spaces[J]. Com put.M ath.App l.,2001,42:313-322.

The multip licity of positive pseudo-symm etricsolutions to a three-point boundary value problem of p-Laplacian equations

TIAN Yuan-sheng

(Department of Mathem atics,X iangnan University,Chenzhou,Hunan,423000,China)

By using Avery-Peterson theorem on convex cone,we consider the three-point boundary value problem for p-Lap lace equations with the nonlinear term depending on the first order derivative,the resutlt of three positive pseudo-symm etric solutions are obtained.

p-Laplacian opertor,three-point boundary value porblem,positive pseudo-symm etric solution, cone

O175.8

A

1008-5513(2009)02-0294-08

2008-07-08.

湖南省教育廳科研項目(08C826),湖南省重點建設(shè)學科項目,湖南省高?？萍紕?chuàng)新團隊計劃項目.

田元生(1962-),副教授,研究方向：微分方程.

2000M SC:34B15