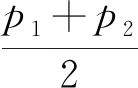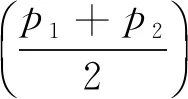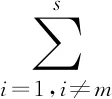UniquenessoftheBestApproximationinaNewHaarTypeSpace*1

The problem of the best approximation with generalized restrictions is considered in this paper.By introducing a new Haar type space,the uniqueness and strong uniqueness of the best approximation on this Haar type space are given.

best approximation;Haar type space;uniqueness;strong uniqueness

1 Introduction

The uniqueness and strong uniqueness of the best approximation have received much attention (ref. [1-9]).In ref. [1],Chalmers and Taylor introduced a general method of investigating uniqueness of best approximations with constraints,which provided a unified approach to the problem.However,this approach essentially provided only sufficient conditions for uniqueness of best constrained approximation.In ref. [4],the authors introduced a new Haar space,namely,LHaar space,and established a Haar type theory for constrained approximation,and gave some necessary and sufficient conditions for uniqueness and strong uniqueness.Note thatIHaar is not Haar as shown in ref. [9].Thus,the authors in ref. [9] introduced another Haar type space and studied the characterization for this Haar type space.

Inspired by those works mentioned above,we continue to study the problem of the best approximation with generalized restrictions.By introducing a new Haar type space defined in ref. [9],we establish the uniqueness and strong uniqueness of the best approximation.

2 L* Haar Spaces

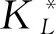
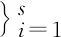
(1)

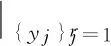
Definition2 It is said thatp∈Unvanishes onAorA*ifp(xi)=0(1≤i≤s) and (Lp)(yj)=0(1≤j≤r).

Definition3UnisL(resp.L*) Haar if nop∈Un{0} vanishes on a nondegenerateL(resp.L*) extremal set forUn.

Letf∈C[a,b] andp∈Un(l,u), we denote

The following definition was introduced in ref. [1].

Definition4 A functionf∈C[a,b]Un(l,u) is said to be admissible if inf{‖f-q‖:q∈Un(l,u)}>max{l(y)-f(x),f(x)-u(y)} holds for eachx∈[a,b] andy∈Kwithex=Ly.

LetCa[a,b] denote the set of all admissible functions.In particular,ifl(y)≤f(x)≤u(y) for allx∈[a,b] andy∈K,thenf∈Ca[a,b].Letf∈C[a,b],p∈Un(l,u),denoteΓ(f,p)=(EX+ (p)∩LK- (p))∪ (EX-(p)∩LK+ (p)).Then we have the following proposition.

Proposition1 The following statements are equivalent:

(ⅰ)f∈Ca[a,b];

(ⅱ) For everyp∈Un(l,u),ifx∈X(p) andy∈K(p) withex=Ly,thenσ1(f,p,x)=σ2(f,p,y);

(ⅲ) For eachp∈Un(l,u),we haveΓ(f,p)=?;

(ⅳ) There existsp0∈Un(l,u) such thatΓ(f,p0)=?;

(ⅴ) There existsp0∈PUn(l,u)(f) such thatΓ(f,p0)=?.

Proof(ⅰ)?(ⅱ).Suppose that (ⅰ) holds and that there existp∈Un(l,u),x∈X(p) andy∈K(p) withex=Ly,butσ1(f,p,x) ≠σ2(f,p,y).Without loss of generality,we assume thatσ1(f,p,x)=-1,σ2(f,p,y)=1,that is,f(x)-p(x)=-‖f-p‖ andLp(y)=l(y).Sincefis admissible,it follows that

max{l(y)-f(x),f(x)-u(y)}<‖f-p‖=ex(p)-f(x)=Ly(p)-f(x)=l(y)-f(x),

which is a contradiction.

(ⅱ)?(ⅲ).Suppose that (ⅱ) holds and that there existsp∈Un(l,u) such thatΓ(f,p)≠ ?.Without loss of generality,we assume thatEX+(p)∩LK-(p)≠ ?,then there existx∈X+(p) andy∈K-(p) such thatex=Ly.But this implies thatσ1(f,p,x)=1 andσ2(f,p,y)=-1 ,which contradicts with (ⅱ).

(ⅲ)?(ⅳ)?(ⅴ) are trivial.

(ⅴ)?(ⅰ).Suppose that (ⅴ) holds and thatfis not admissible.Then for everyp∈PUn(l,u)(f),x∈[a,b] andy∈Kwithex=Ly,one has ‖f-p0‖≤max{l(y)-f(x),f(x)-u(y)}.Note that

f(x)-u(y)≤f(x)-Lp0(y)=f(x)-p0(x)≤‖f-p0‖

(2)

and

l(y)-f(x) ≤Lp0(y)-f(x)=p0(x)-f(x) ≤‖f-p0‖.

Then

‖f-p0‖≤max{l(y)-f(x),f(x)-u(y)}≤‖f-p0‖.

(3)

Thus,the equalities in (3) must hold.

(a) Iff(x)-u(y)=‖f-p0‖,then,by (2),we haveu(y)=Lp0(y) andf(x)-p0(x)=‖f-p0‖.This meansx∈X+(p0) andy∈K-(p0).Hence,EX+(p0)∩LK-(p0)≠ ?,contradicting with (ⅴ).

(b) Similarly,ifl(y)-f(x)=‖f-p0‖,then we haveEX-(p0)∩LK+(p0)≠ ?,contradicting with (ⅴ).The proof is complete.

Definition5 Letf∈C[a,b] andp∈Un,theL*extremal setA*is said to be anL*extremal set with respect to (f,p) (denote byA*(f,p)),ifxi,yj,ci,djin (1) satisfy the following conditions:

(ⅰ)xi∈X(p),yj∈K(p);

(ⅱ) sgnci=σ1(f,p,xi),i=1,2,...,s;

(ⅲ) sgndj=σ2(f,p,yj),j=1,2,...,r.

Proposition2 Letf∈Ca[a,b],p0∈PUn(l,u)(f).IfUnis anL*Haar space,then there exists a nondegenerateL*extremal setA*(f,p0) forUn.

ProofLetf∈Ca[a,b],p0∈PUn(l,u)(f).Then,by ref. [9,theorem 3.1],there exist points {x1,...,xs}?X(p0),{y1,...,yr}?K(p0)(s+r≤n+1) andc1,...,cs,d1,...,dr≠ 0 such that

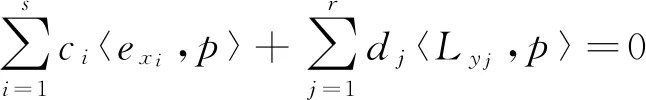
(4)

3 Uniqueness of the Best Approximation

Theorem1 LetUnbe anL*Haar space,then for everyf∈Ca[a,b] andl,u∈C(K) withl(t)

(5)

Below we show that

(6)

(7)

In order to establish some results on the strong uniqueness of the best approximation fromUn(l,u),we first introduce the concept of the strong uniqueness of orderγ>0;see,for example,ref. [4,8].

Definition6 Suppose thatf∈C[a,b],p0∈PUn(l,u)(f).It is said thatp0is strongly unique of orderγ>0 if there exists a constantα=α(f) such that ‖f-p‖γ≥‖f-p0‖γ+α‖p-p0‖γ，p∈Un(l,u).In the case whenγ=1 we simply say thatp0is strongly unique.

Theorem2 LetUnbe anL*Haar space.Then for everyf∈Ca[a,b] andl,u∈C(K) withl(t)

Letp1∈Un(l,u) be such that ‖f-p1‖=‖f-p0‖+with 1>>0.Since (f-p0)(xi)= (sgnci)‖f-p0‖,i=1,...,s,it follows that

sgnci(p0-p1)(xi)= sgnci(f-p1)(xi)-sgnci(f-p0)(xi)≤

‖f-p1‖-‖f-p0‖=.

(8)

Furthermore,y1,...,yl∈K-(p0),yl+1,...,yr∈K+(p0) yield

L(p0-p1)(yj)≥0(j=1,...,l),L(p0-p1)(yj)≤0 (j=l+1,...,r).

(9)

Letp*=p0-p1∈Un,by (8)

(10)

Moreover,(9) yields thatdjLp*(yj)≤0 (j=1,...,r).Taking also into account (10) we have

|Lp*(yj)|≤M1j=1,...,r,

(11)

This together with (8) implies

|p*(xi)|≤M2i=1,...,s,

(12)

By the equivalence of norms in finite dimensional spaces,there exists constantM3>0 such that

‖p0-p1‖=‖p*‖≤M3N(p*)≤c=c(‖f-p1‖-‖f-p0‖),

[1] CHALMERS B L,TAYLOR G D.A Unified Theory of Strong Uniqueness in Uniform Approximation with Constraints[J].J. Approx.Theory,1983(37):29-43.

[2] CULBERTSON J.On Approximation by Monotone Polynomials in the Chebyshev Norm Characterization and Uniqueness[D].Master’s Thesis University of Maryland,1968.

[3] FANG Donghui,LI Chong,YANG Wenshan.Strong CHIP and Characterization of the Best Approximation with Generalized Restrictions[J].Acta Mathematica Sinica,2004,47(6):1 115-1 123.(in Chinese)

[5] SHI Yingguang.The Limits of a Chebyshev Type Theory of Restricted Range Approximation[J].J. Approx. Theory,1988,53:41-53.

[6] SINGER I.Best Approximation by Elements of Linear Subspaces in Linear Spaces[M].New York:Spring Verleg,1974.

[7] RICE J R.The Approximation Functions[M].London:Addison Wesley,1964.

[8] XU Shiying,LI Chong,YANG Wenshan.The Theory of Nonlinear Approximation in Banach Spaces[M].Beijing:Science Press,1997.(in Chinese)

[9] WANG Xianyun,FANG Donghui.Characterizations forLHaar Space[J].Journal of Jishou University:Natural Sciences Edition,2005(1):12-14.(in Chinese)

(責(zé)任編輯 向陽潔)

FANG Donghui

(College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)

一類新的Haar子空間中最佳逼近的唯一性

方東輝

(吉首大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,湖南 吉首 416000)

研究了廣義限制域最佳逼近問題.引入一個(gè)L*Haar子空間的概念,建立了該Haar子空間中最佳逼近的唯一性和強(qiáng)唯一性.

最佳逼近;L*Haar子空間;唯一性;強(qiáng)唯一性

O174.41

A

1007-2985(2014)04-0008-05

date：2014-05-01

Supported by National Natural Science Foundation of China (11101186);Scientific Research Fund of Hunan Provincial Education Department (13B095)

Biography：FANG Donghui(1979-),male,was born in Dongkou County,Hunan Province,doctor,associate professor at Jishou University,research area are nonsmooth analysis and nonlinear optimization.

O174.41DocumentcodeA

10.3969/j.issn.1007-2985.2014.04.002