白榮榮, 吳洪博

(陜西師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 陜西 西安 710119)

根據(jù)研究對(duì)象的不同,拓?fù)鋵W(xué)的研究方法可以分為有點(diǎn)化方法和無(wú)點(diǎn)化方法[1-2].兩種方法各有其特點(diǎn)與優(yōu)勢(shì),可以相互借鑒[3-6].1989年,Vickers[7]引進(jìn)了一種新型的拓?fù)鋵W(xué)研究對(duì)象-拓?fù)湎到y(tǒng),成功的將兩種方法融合為一體.Vickers[7]主要從格序理論方面對(duì)拓?fù)湎到y(tǒng)的性質(zhì)和應(yīng)用進(jìn)行了討論.近幾年來(lái),國(guó)內(nèi)學(xué)者對(duì)拓?fù)湎到y(tǒng)的性質(zhì)和應(yīng)用均有研究,并且取得了一些相關(guān)成果[8-16].

本文結(jié)合拓?fù)淇臻g中開(kāi)集和拓?fù)湎到y(tǒng)中開(kāi)元的關(guān)聯(lián)性,在拓?fù)湎到y(tǒng)中提出了內(nèi)部元的概念,并對(duì)其相關(guān)性質(zhì)進(jìn)行了研究.本文的工作主要包含三部分:1) 在拓?fù)湎到y(tǒng)中引入內(nèi)部元概念,討論了內(nèi)部元的基本性質(zhì);2) 在點(diǎn)集X與FrameA之間通過(guò)映射范圍Ex:A→2X,內(nèi)部元映射Int:2X→A定義了內(nèi)部元算子,討論了內(nèi)部元算子的相關(guān)性質(zhì),給出了由內(nèi)部元算子確定拓?fù)湎到y(tǒng)的方法;3) 利用內(nèi)部元對(duì)拓?fù)湎到y(tǒng)之間的連續(xù)映射進(jìn)行了等價(jià)刻畫(huà).

1 預(yù)備知識(shí)

定義1[3,7]FrameA是滿足以下條件的偏序集:

1) ?S?finA,S的下確界存在,即∧S存在;

2) ?S?A,S的上確界存在,即∨S存在;

3) 滿足第一無(wú)限分配律,即,?a∈A,?S?A,有a∧(∨S)=∨{a∧s:s∈S}.

注11) 本文中S?finA表示S是A中的有限子集;

2) 由于∨-完備格是完備格,完備格是有界格,將其中最大元記作1,最小元記作0.又在格中兩個(gè)分配律等價(jià),因此Frame是分配格.

定義2[3,7]設(shè)A,B是Frame.若映射f:A→B滿足以下條件:

1) ?S?finA,f(∧S)=∧f(S);

2) ?S?A,有f(∨S)=∨f(S);

則稱f:A→B是Frame同態(tài).

定義3[7]設(shè)A是Frame,X是集合,|=?X×A,若(x,a)∈|=,則稱x滿足a,記作x|=a.若|=滿足:

1)?S?finA,?x∈X,x|=∧S??a∈S,x|=a;

2)?S?A,?x∈X,x|=∨S??a∈S,使得x|=a;

則稱(X,A,|=)為一個(gè)拓?fù)湎到y(tǒng).

在本文中,將拓?fù)湎到y(tǒng)(X,A,|=)記為D,將X記為PtD,將A記為ΩD.

引理1[7]設(shè)D=(PtD,ΩD,|=)是拓?fù)湎到y(tǒng),1,0分別是ΩD的最大元和最小元.?a,b∈ΩD,則

1) ?x∈PtD,x|=1;

2) ?x∈PtD,x|≠0;

3) 若x|=a,a≤b,則x|=b.

引理2[7]設(shè)D=(PtD,ΩD,|=)是拓?fù)湎到y(tǒng).定義映射ex:ΩD→2PtD,

?a∈ΩD,ex(a)={x∈PtD,x|=a}

設(shè)Ω(PtD)={ex(a)|a∈ΩD},則Ω(PtD)是PtD上的拓?fù)?并且,

1) ex(0)=?,ex(1)=2PtD;

2) ?a,b∈ΩD,ex(a∧b)=ex(a)∩ex(b);

3) ?S?ΩD,ex(∨S)=∪{ex(s)|s∈S}.

2 拓?fù)湎到y(tǒng)中的內(nèi)部元及基本性質(zhì)

借助拓?fù)湎到y(tǒng)中的Frame的成員定義拓?fù)湎到y(tǒng)中點(diǎn)集部分的子集的內(nèi)部元, 并討論與內(nèi)部元相關(guān)的性質(zhì).

定義4在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中,設(shè)A?PtD.令

A°=∨{a|a∈ΩD,ex(a)?A}

稱A°為集合A在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中的內(nèi)部元.

定理1在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中,內(nèi)部元有如下的性質(zhì):

1) ex(1)=PtD,(PtD)°=1;

2) ?A?PtD,ex(A°)?A;

3) ?A,B?PtD,若A?B,則A°≤B°;

4) ?A,B?PtD,A°∧B°=(A∩B)°;

5) ?a∈ΩD,a≤(ex(a))°;

6) ?A?PtD,a∈ΩD,則ex(a)?ex(A°)當(dāng)且僅當(dāng)a≤A°;

7) ?A?PtD,(ex(A°))°=A°;

8) ?a∈ΩD,ex((ex(a))°)=ex(a).

證明在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中,

1) 由引理1中1)知?x∈PtD,x|=1.即,?x∈PtD,x∈ex(1).因此,ex(1)=PtD.

因?yàn)?a∈ΩD,則a≤1,結(jié)合引理2中2)可知:ex(a)?ex(1)=PtD.所以,由定義4得

(PtD)°=∨{a|a∈ΩD,ex(a)?PtD}=
∨{a|a∈ΩD}=1

2) ?A?PtD,根據(jù)定義4,引理2中3)得

ex(A°)=ex(∨{a|a∈ΩD,ex(a)?A})=
∪{ex(a)|a∈ΩD,ex(a)?A}?A

3) ?A,B?PtD,若A?B,因此,

{a|a∈ΩD,ex(a)?A}?

{a|a∈ΩD,ex(a)?B}

因此,

∨{a|a∈ΩD,ex(a)?A}≤

∨{a|a∈ΩD,ex(a)?B}

因此,

A°≤B°

4) ?A,B?PtD.首先,由于A∩B?A,根據(jù)3)得

A°≥(A∩B)°;同理,B°≥(A∩B)°

其次,由2)知:ex(A°)?A,ex(B°)?B,因此,A°∧B°≥(A∩B)°,

ex(A°)∩ex(B°)?A∩B

結(jié)合引理2中2)得

ex(A°∧B°)?A∩B

因此,A°∧B°∈{a|a∈ΩD,ex(a)?A∩B},再結(jié)合定義4得

(A∩B)°=∨{a|a∈ΩD,ex(a)?A∩B}≥A°∧B°

綜合以上兩方面得

A°∧B°=(A∩B)°

5) ?a∈ΩD,因?yàn)閍∈{b|b∈ΩD,ex(b)?ex(a)},因此,根據(jù)定義4得

(ex(a))°=∨{b|b∈ΩD,ex(b)?ex(a)}≥a

6) 設(shè)A?PtD,a∈ΩD.

一方面,若ex(a)?ex(A°),又由定理1中2)得

ex(A°)?A

因此,ex(a)?A.結(jié)合3)得

(ex(a))°≤A°

又根據(jù)5)得

a≤(ex(a))°

因此,a≤A°.

另一方面,若a≤A°,結(jié)合引理2中2)可得

ex(a)?ex(A°)

結(jié)合兩方面得ex(a)?ex(A°)當(dāng)且僅當(dāng)a≤A°.

7) ?A?PtD,首先,A°∈ΩD,其次,A°≤A°,利用6)得

8) ?a∈ΩD,由2)得ex((ex(a))°)?ex(a);由5)得a≤(ex(a))°,由范圍映射的保序性直接可得ex(a)?ex((ex(a))°),所以,ex((ex(a))°)=ex(a).

定理2在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中,

{A°|A∈2PtD}={(ex(a))°|a∈ΩD}

證明一方面,?a∈ΩD,由于ex(a)∈2PtD,因此,?a∈ΩD,(ex(a))°∈{A°|A∈2PtD}.所以,

{A°|A∈2PtD}?{(ex(a))°|a∈ΩD}

另一方面,?A∈2PtD,由定理1中7)得(ex(A°))°=A°.又由于A°∈ΩD,因此,

(ex(A°))°∈{(ex(a))°|a∈ΩD}

兩者結(jié)合得A°∈{(ex(a))°|a∈ΩD}.所以,

{A°|A∈2PtD}?{(ex(a))°|a∈ΩD}

綜合以上兩方面得

{A°|A∈2PtD}={(ex(a))°|a∈ΩD}

定理3在拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)中,

{A∈2PtD|ex(A°)=A}={ex(a)|a∈ΩD}

證明一方面,?A∈2PtD,如果ex(A°)=A,由于A°∈ΩD,因此,ex(A°)∈{ex(a)|a∈ΩD},從而,A∈{ex(a)|a∈ΩD}.所以,

{A∈2PtD|ex(A°)=A}?{ex(a)|a∈ΩD}

另一方面,?a∈ΩD,由定理1中8)知:

ex((ex(a))°)=ex(a)

因此,ex(a)∈{A∈2PtD|ex(A°)=A}.所以,

{A∈2PtD|ex(A°)=A}?{ex(a)|a∈ΩD}

綜合以上兩方面知:

{A∈2PtD|ex(A°)=A}={ex(a)|a∈ΩD}

3 拓?fù)湎到y(tǒng)中的內(nèi)部元算子

定義5(內(nèi)部元算子) 設(shè)X是非空集合,L是Frame.若雙映射:Ex:L→2X,Int:2X→L滿足條件:

1) Int(X)=1,Ex(1)=X;

2) ?A?X,A?Ex(Int(A));

3) ?a,b∈L,Ex(a∧b)=Ex(a)∩Ex(b);

4) ?A,B?X,Int(A)∧Int(B)=Int(A∩B);

5) ?a∈L,Int(Ex(a))≥a;

則稱(Ex,Int)是(X,L)上的內(nèi)部元算子.

引理3設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.則

1) Ex:L→2X是保序映射.即,?a,b∈L,若a≤b,則Ex(a)?Ex(b);

2) Int:2X→L是保序映射.即,?A,B∈2X,若A?B,則Int(A)≤Int(B);

3) ?A∈2X,Int(Ex(Int(A)))=Int(A);

4) ?a∈ΩD,Ex(Int(Ex(a)))=Ex(a);

證明1) ?a,b∈L.若a≤b,則a∧b=a.因此,Ex(a∧b)=Ex(a).結(jié)合定義5中3)得

Ex(a)∩Ex(b)=Ex(a)

因此,Ex(a)?Ex(b).

2) 類似1)的證明,結(jié)合定義5中4)可證,略.

3) 一方面,由內(nèi)部算子的條件2)得

Ex(Int(A))?A

結(jié)合引理3中2)可得

Int(Ex(Int(A)))≤Int(A)

另一方面,由內(nèi)部算子的條件5)得

Int(Ex(Int(A)))≥Int(A)

綜合兩方面得

Int(Ex(Int(A)))=Int(A)

4) ?a∈ΩD.由定義5中2)得

Ex(Int(Ex(a)))?Ex(a)

由定義5中5)得Int(Ex(a))≥a,結(jié)合引理3中1)得

Ex(Int(Ex(a)))?Ex(a)

所以,Ex(Int(Ex(a)))=Ex(a)

引理4設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.則集族

Τ={A∈2X|Ex(Int(A))=A}

是集合X上的拓?fù)?

證明1) 由定義5中1)得

Ex(Int(X))=Ex(1)=X

因此,X∈Τ;

再由定義5中2)得??Ex(Int(?)),因此,?=Ex(Int(?)),因此,?∈Τ;

2) 設(shè)A,B∈Τ,則

A=Ex(Int(A)),B=Ex(Int(B))

結(jié)合定義5中3),定義5中4)得

Ex(Int(A∩B))=Ex(Int(A)∧Int(B))=

Ex(Int(A))∩Ex(Int(B))=A∩B

因此,A∩B∈Τ;

3) 設(shè){Aj|j∈J}?Τ,則

?j∈J,Aj=Ex(Int(Aj))

一方面,由定義5中2)得

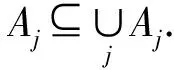
進(jìn)而,

再結(jié)合?j∈J,Aj=Ex(Int(Aj))得

因此,

綜合上面兩方面得

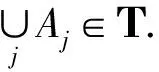
由1)～3)的結(jié)果知:集族

Τ={A∈2X|Ex(Int(A))=A}

是集合X上的拓?fù)?

引理5設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.則Ex:L→2X是Frame同態(tài).

證明1) ?a,b∈L.根據(jù)定義5中3)可得

Ex(a∧b)=Ex(a)∩Ex(b)

2) ?{aj|j∈J}?L.

一方面,由于?j∈J,aj≤∨{aj|j∈J}.結(jié)合引理3中1)得

?j∈J,Ex(aj)?Ex(∨{aj|j∈J})

因此,

∪{Ex(aj)|j∈J}?Ex(∨{aj|j∈J})

另一方面,由于?j∈J,

∪{Ex(aj)|j∈J}?Ex(aj)

由引理3中2)得?j∈J,

Int(∪{Ex(aj)|j∈J})≥Int(Ex(aj))

又由定義5中5)得

?j∈J,Int(Ex(aj))≥aj

將兩者結(jié)合得

Int(∪{Ex(aj)|j∈J})≥aj

因此,

Int(∪{Ex(aj)|j∈J})≥∨{aj|j∈J}

結(jié)合引理3中1)得

Ex(Int(∪{Ex(aj)|j∈J}))?Ex(∨{aj|j∈J})

再由定義5中2)得

∪{Ex(aj)|j∈J}?Ex(Int(∪{Ex(aj)|j∈J}))

因此,由傳遞性得

∪{Ex(aj)|j∈J}?Ex(∨{aj|j∈J})

綜合以上兩方面得

∪{Ex(aj)|j∈J}=Ex(∨{aj|j∈J})

因此,根據(jù)定義2知Ex:L→2X是Frame同態(tài).

引理6設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.定義從X到L的二元關(guān)系|=如下:

?(x,a)∈X×L,x|=a當(dāng)且僅當(dāng)x∈Ex(a)

則(X,L,|=)是拓?fù)湎到y(tǒng).

證明由引理5知:Ex:L→2X是Frame同態(tài).下面驗(yàn)證二元關(guān)系|=滿足定義3中1)和2).

1) ?S?finL,結(jié)合定義5中3)得x|=∧S,當(dāng)且僅當(dāng)x∈Ex(∧S),當(dāng)且僅當(dāng)x∈∩{Ex(s)|s∈S},當(dāng)且僅當(dāng)?s∈S,x∈Ex(s),當(dāng)且僅當(dāng)?s∈S,x|=s;

2) ?S?L,由引理5知:

Ex(∨S)=∪{Ex(s)|s∈S}

因此,x|=∨S,當(dāng)且僅當(dāng)x∈Ex(∨S),當(dāng)且僅當(dāng)x∈∪{Ex(s)|s∈S},當(dāng)且僅當(dāng)?s∈S,x∈Ex(s),當(dāng)且僅當(dāng)?s∈S,x|=s.

根據(jù)定義3知:(X,L,|=)是拓?fù)湎到y(tǒng).

4 Kuratovski型內(nèi)部元算子定理

定理4(內(nèi)部元算子定理) 設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.則存在唯一的拓?fù)湎到y(tǒng)D=(X,L,|=),使得在該拓?fù)湎到y(tǒng)中,?A?X,A°=Int(A).

證明設(shè)X是非空集合,L是Frame,(Ex,Int)是(X,L)上內(nèi)部元算子.定義從X到L的二元關(guān)系“|=”如下:

?(x,a)∈X×L,x|=a當(dāng)且僅當(dāng)x∈Ex(a)

則由引理6知D=(X,L,|=)是拓?fù)湎到y(tǒng),且由“|=”定義和引理2可知:?a∈L,

ex(a)=Ex(a)

在拓?fù)湎到y(tǒng)(X,L,|=)中,?A∈2X,由定義4知:A°=∨{a|a∈L,Ex(a)?A}.

一方面,由定義5中2)知:Ex(Int(A))?A,又Int(A)∈L,因此,

Int(A)∈{a|a∈L,Ex(a)?A}

另一方面,?a∈L,若Ex(a)?A,則結(jié)合引理3中2)可得Int(A)≥Int(Ex(a));又由定義5中5)得Int(Ex(a))≥a.因此,Int(A)≥a.

綜合兩方面知:

A°=∨{a|a∈L,Ex(a)?A}=Int(A)

下面證明滿足條件的拓?fù)湎到y(tǒng)D=(X,L,|=)的唯一性,若拓?fù)湎到y(tǒng)D1=(X,L,|=1)也滿足:

?A?PtD,A°=Int(A)

在拓?fù)湎到y(tǒng)D1=(X,L,|=1)中,?a∈L,用ex1(a)記a在D1中的范圍,因此,

1) (ex1(a))°=Int(ex1(a));

2) (Ex(a))°=Int(Ex(a)).

先證?a∈L,ex1(a)=Ex(a).

?a∈L.

一方面,由定理1中5)得(ex1(a))°≥a,再結(jié)合1)得

a≤Int(ex1(a))

再結(jié)合引理3中1)得

Ex(a)?Ex(Int(ex1(a)))

又根據(jù)定義5中2)得

Ex(Int(ex1(a)))?ex1(a)

因此,

Ex(a)?ex1(a)

另一方面,由定義5中5)得Int(Ex(a))≥a,再結(jié)合2)得

(Ex(a))°≥a

再結(jié)合引理2可知:

ex1((Ex(a))°)?ex1(a)

又根據(jù)定理1的2),得

ex1((Ex(a))°)?Ex(a)

因此,Ex(a))?ex1(a).

綜合以上兩方面得

?a∈L,Ex(a)=ex1(a)

再證|=1=|=.?a∈L,?x∈X.

由引理2知:

x|=1a當(dāng)且僅當(dāng)x∈ex1(a)

結(jié)合Ex(a)=ex1(a)可知:

x|=1a當(dāng)且僅當(dāng)x∈Ex(a)

由|=的定義可知:

x∈Ex(a)當(dāng)且僅當(dāng)x|=a

因此,?a∈L,?x∈X.x|=1a當(dāng)且僅當(dāng)x|=a.所以,|=1=|=.

因此,兩個(gè)拓?fù)湎到y(tǒng)是一致的.

5 連續(xù)映射的等價(jià)刻畫(huà)

利用內(nèi)部元對(duì)連續(xù)映射進(jìn)行等價(jià)刻畫(huà).

定義6[7]設(shè)D=(PtD,ΩD,|=),E=(PtE,ΩE,|=)是拓?fù)湎到y(tǒng),映射Ptf:PtD→PtE和Frame態(tài)射Ωf:ΩE→ΩD構(gòu)成的偶對(duì)(Ptf,Ωf)稱為從拓?fù)湎到y(tǒng)D=(PtD,ΩD,|=)到拓?fù)湎到y(tǒng)E=(PtE,ΩE,|=)的映射,記作f:D→E.

再若?x∈PtD,?b∈ΩD,

x|=Ωf(b)當(dāng)且僅當(dāng)Ptf(x)|=b

則稱f:D→E是連續(xù)映射.

為后面討論方便,先給出下面的連續(xù)映射的等價(jià)描述.

定理5設(shè)D=(PtD,ΩD,|=),E=(PtE,ΩE,|=)是拓?fù)湎到y(tǒng),映射f:D→E連續(xù)的充要條件是:?b∈ΩD,

ex(Ωf(b))=(Ptf)-1(ex(b))

證明必要性) 設(shè)f:D→E是連續(xù)的.?b∈ΩD.

根據(jù)引理2定義6和f:D→E連續(xù)可得?x∈PtD,x∈ex(Ωf(b)),當(dāng)且僅當(dāng)x|=Ωf(b)當(dāng)且僅當(dāng)Ptf(x)|=b,當(dāng)且僅當(dāng)Ptf(x)∈ex(b),當(dāng)且僅當(dāng)x∈(Ptf)-1(ex(b)).

因此,?b∈ΩD,

ex(Ωf(b))=(Ptf)-1(ex(b))

充分性) 設(shè)?b∈ΩD,

ex(Ωf(b))=(Ptf)-1(ex(b))

?b∈ΩD,?x∈PtD.

根據(jù)引理2和ex(Ωf(b))=(Ptf)-1(ex(b))可得x|=Ωf(b)當(dāng)且僅當(dāng)x∈ex(Ωf(b)),當(dāng)且僅當(dāng)x∈(Ptf)-1(ex(b)),當(dāng)且僅當(dāng)Ptf(x)∈ex(b),當(dāng)且僅當(dāng)Ptf(x)|=b.

因此,?b∈ΩD,?x∈PtD,x∈ex(Ωf(b))當(dāng)且僅當(dāng)Ptf(x)|=b.

因此,根據(jù)定義6可知:映射f:D→E是連續(xù)映射.

定理 6設(shè)D=(PtD,ΩD,|=),E=(PtE,ΩE,|=)是拓?fù)湎到y(tǒng),f:D→E是連續(xù)映射.則以下結(jié)論成立.

1) ?U?PtE,ex(Ωf(U°))=(Ptf)-1(ex(U°));

2) ?U?PtE,ex(Ωf(U°))?ex(((Ptf)-1(U))°);

3) ?b∈ΩE,ex(Ωf((ex(b))°))=ex(Ωf(b)).

證明1) ?U?PtE,

由定義4知:U°∈ΩE,已知f:D→E是連續(xù)映射,因此由定理5直接得

ex(Ωf(U°))=(Ptf)-1(ex(U°)).

2) ?U?PtE,?x∈PtD.

若x∈ex(Ωf(U°)),由引理2中ex:ΩD→2PtD的定義可知:Ptf(x)|=U°.因此,Ptf(x)∈ex(U°).結(jié)合定義4和引理2可知:

?b∈ΩE使得Ptf(x)∈ex(b)?U.

因此,?b∈ΩE使得

x∈(Ptf)-1(ex(b))?(Ptf)-1(U)

由于f:D→E是連續(xù)映射,由定理5可得

ex(Ωf(b))=(Ptf)-1(ex(b))

因此,?b∈ΩE使得

x∈ex(Ωf(b))?(Ptf)-1(U)

根據(jù)定義4可知:x∈ex(((Ptf)-1(U))°).因此,

ex(Ωf(U°))?ex(((Ptf)-1(U))°)

3) ?b∈ΩE,由定理1中8)得ex((ex(b))°)=ex(b),又f:D→E是連續(xù)映射,結(jié)合定理5得

ex(Ωf((ex(b))°))=

(Ptf)-1(ex((ex(b))°))=

(Ptf)-1(ex(b))=ex(Ωf(b))

推論1設(shè)D=(PtD,ΩD,|=),E=(PtE,ΩE,|=)是拓?fù)湎到y(tǒng),f:D→E是連續(xù)映射,U?PtE.則

(Ptf)-1(ex(U°))?ex(((Ptf)-1(U))°)

證明結(jié)合定理6中1)和2)直接可得.

定理7設(shè)D=(PtD,ΩD,|=),E=(PtE,ΩE,|=)是拓?fù)湎到y(tǒng),映射f:D→E連續(xù)的充要條件是下面1)和2)同時(shí)成立:

1) ?U?PtE,ex(Ωf(U°))=(Ptf)-1(ex(U°))

2) ?b∈ΩE,ex(Ωf((ex(b))°))?ex(Ωf(b))

證明必要性) 根據(jù)定理6中1)和3)直接可得.

充分性) ?b∈ΩE,則ex(b)?PtE,代入1)得

ex(Ωf((ex(b))°))=(Ptf)-1(ex((ex(b))°))

又根據(jù)定理1中8)得ex((ex(b))°)=ex(b),因此,

ex(Ωf((ex(b))°))=(Ptf)-1(ex(b));

再根據(jù)定理1中5)得(ex(b))°≥b,結(jié)合Ωf:ΩE→ΩD和ex:ΩD→2PtD的保序性可得

ex(Ωf((ex(b))°))?ex(Ωf(b))

結(jié)合2)得

ex(Ωf((ex(b))°))=ex(Ωf(b))

結(jié)合上面的等式得

?b∈ΩE,ex(Ωf(b))=(Ptf)-1(ex(b))

因此,根據(jù)定理5可知:映射f:D→E是連續(xù)映射.