洪濤清,張劍鋒

(麗水學院 數(shù)學系,浙江 麗水 323000)

隨著分析方法的發(fā)展,學者們對黎曼幾何的研究越來越深刻,關(guān)于它的相關(guān)結(jié)論與證明方法也得到不斷更新.近來學者們對常曲率空間中各類子流形幾何的研究取得了非常重要的研究成果,特別是球面Sn+p(a)中的極小子流形.J.Simons建立了關(guān)于Sn+p(a)中極小子流形的第二基本形式模長平方的積分不等式[1]

(1)

其中:dv表示Mn的體積元素;S是第二基本形式的模長平方,即S=‖B‖2.

J.Simons積分不等式對子流形幾何的研究和發(fā)展有很大影響.應(yīng)用J.Simons方法,可以建立各種非空間形式各類子流形的J.Simons型積分不等式[2-4].將J.Simons積分不等式推廣到非空間形式中各類子流形,成為子流形幾何中重要的研究課題.

Chen[5]提出了擬常曲率空間的概念,它是常曲率空間的推廣.對于擬常曲率空間中的極小子流形,Bai[6]建立了J.Simons型積分不等式.宋衛(wèi)東[7]研究了擬常曲率空間中的2-調(diào)和子流形,給出了類似的積分不等式.

Gazi等[8]將擬常曲率空間的概念推廣到近擬常曲率空間,并給出了近擬常曲率空間但不是擬常曲率空間的例子,論文給出了這個例子的證明.

Su等[9]利用代數(shù)引理和基本方程,建立了近擬常曲率空間中雙重卷積子流形關(guān)于Ricci曲率和平均曲率的幾何不等式.耿杰等[10]建立了近擬常曲率空間具有常平均曲率超曲面的Pinching定理.

論文主要研究近擬常曲率空間中的極小子流形,建立了近擬常曲率空間中的極小子流形關(guān)于其第二基本形式模長平方S的J.Simons型積分不等式,主要結(jié)果為定理A.

定理A設(shè)Mn是近擬常曲率空間中Nn+p緊致極小子流形,則成立下列積分不等式

(2)

其中:a,b為Nn+p上的連續(xù)函數(shù);dv為Mn的體積元素;S為Mn第二基本形式的模長平方‖B‖2.

1 定理A的證明

4={(x1,x2,x3,x4)|xi∈},

g=gijdxidxj=(x4)4/3[(dx1)2+(dx2)2+(dx3)2]+(dx4)2,

在其余情況下,KABCD=0,其黎曼曲率可表示為

KABCD=a(gACgBD-gADgBC)+b(gACfBD+gBDfAC-gADfBC-gBCfAD),

其中

定理A的證明.設(shè)(Nn+p,g)表示其黎曼曲率張量,取如下形式

KABCD=a(gACgBD-gADgBC)+b(gACλBλD-gBDλAλC-gADλBλC-gBCλAλD),

(3)

的n+p維單連通完備黎曼流形,稱為擬常曲率空間[8].其中:g是Nn+p的黎曼度量;a,b是Nn+p上c∞-函數(shù);{λA}是Nn+p上一個單位向量函數(shù).顯然,擬常曲率空間是常曲率空間的推廣.

若(Nn+p,g)表示其黎曼曲率張量,取如下形式

KABCD=a(gACgBD-gADgBC)+b(gACfBD+gBDfAC-gADfBC-gBCfAD),

(4)

的n+p維單連通完備的黎曼流形,稱為近擬常曲率空間[8].其中:g是Nn+p的黎曼度量;a,b為Nn+p上c∞-函數(shù);{fAB}是Nn+p上一個單位向量函數(shù).

顯然,當fAB可解為λAλB,即fAB=λAλB時,近擬常曲率空間就是擬常曲率空間.

設(shè)Nn+p是n+p維單連通完備的近擬常曲率空間,Mn是Nn+p上n維的緊致極小子流形,在Nn+p上選取局部正交標架{eA}限制在Mn上,{ei}與Mn相切.

約定各類指標的取值范圍

1≤A,B,C…≤n+p,1≤i,j,k,…≤n,n+1≤α,β,γ,…≤n+p,

在此標架下,由式(4)可得Nn+p的曲率張量為

KABCD=a(δACδBD-δADδBC)+b(δACfBD+δBDfAC-δADfBC-δBCfAD),

(5)

顯然,有

Kαβjk=0.

(6)

設(shè){ωA}及{ωAB}是{eA}的對偶標架及聯(lián)絡(luò)1-形式,限制在Mn上,有

(7)

(8)

Mn的第二基本形式模長‖B‖及Mn的平均曲率H分別記為

(9)

仿文獻[1],有

(10)

其中

下面,估計式(10)中A1,A2,A3,A4,A5.

由式(6),有

A5=0.

(11)

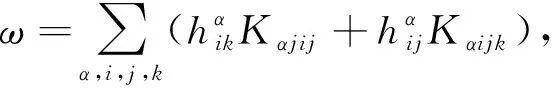
有

有

(12)

現(xiàn)在估計A2,由式(5)及Mn為極小子流形H=0,有

由Cauchy不等式,得

有

于是

(13)

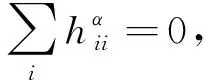
(14)

又因為矩陣(trHαHβ)p×p是實對稱矩陣,所以可使矩陣對角化,即

從而由文獻[11],有

(15)

由(14),(15),有

(16)

結(jié)合式(10)～(16)以及Green散度定理,得

(17)

由于Mn的緊致性,對式(20)兩邊積分,應(yīng)用Stokes定理,得

即完成了定理A的證明.