兩集合并集可測和原集合自身可測的關(guān)系
林鑫宇, 李文娟
(1.西北工業(yè)大學(xué) 教育實(shí)驗(yàn)學(xué)院,西安 710129; 2.西北工業(yè)大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,西安 710129)
1 問題產(chǎn)生
實(shí)變函數(shù)是一門重要的數(shù)學(xué)專業(yè)課,抽象性高,學(xué)習(xí)難度大.反例的研究可以幫助更好的理解定義和定理.有鑒于此,國內(nèi)許多學(xué)者對實(shí)變函數(shù)的反例研究已有了不少成果[1-2].
可測函數(shù)和Lebesgue積分是實(shí)變函數(shù)中的重要概念.教材[3]中提到為了構(gòu)造Lebesgue積分,要求函數(shù)f(x)滿足:?a,b∈,E={x∈n;a≤f(x)≤b}是可測的;而可測函數(shù)的定義卻要求函數(shù)f(x)滿足:?a∈,E={x∈n;f(x)≥a}是可測的.這兩個條件是否等價呢?顯然前者是后者的必要條件,那么前者是否還是后者的充分條件呢?下面嘗試由前者推出后者.
設(shè)f(x)是定義在可測集E上的函數(shù),滿足?a,b∈,Eab∶={x∈n;a≤f(x)≤b}可測.此時,可證?a∈,n;a≤f(x)<+∞}可測,所以要證明?a∈,Ea={x∈n;f(x)≥a}可測,只要證明E+∶={x∈n;f(x)=+∞}可測.考慮到集合E*∶={x∈n;-∞ 定義1[4]設(shè)集合E?n.若對任意的點(diǎn)集T?n,有 m*(T)=m*(T∩E)+m*(T∩Ec), 則稱集合E是Lebesgue可測的. 定義2設(shè)集合A,B?n,若?開集VA?A,開集VB?B,使得VA∩VB=?,則稱A,B是隔離的. 定理1下列三個命題是等價的: (i)A,B是隔離的; (ii)A∩B=?B∩A=?A∩B=?,其中?A表示集合A的邊界; 證(i)推(ii) 因?yàn)锳,B是隔離的,所以?開集GA?A,開集GB?B,使得 GA∩GB=?. (1) A∩B=?是顯然的. 事實(shí)上,還有?B∩A=?,不然,?t∈?B∩A.現(xiàn)任取開集VA?A,開集VB?B.因?yàn)閠∈?B∩A?A?VA及VA是開集,所以?δ>0,使N(t,δ)?VA,從而VA∩VB?N(t,δ)∩B.又因?yàn)閠∈?B∩A??B,所以對上述δ>0,N(t,δ)∩B≠?,因此VA∩VB≠?.考慮到VA,VB具有任意性,這與(1)矛盾. 同理,?A∩B=?. 同理,對?y∈B,?δy>0,使 N(y,δy)∩A=?. (2) 從而x0∈N(y0,δy0)∩A,這與(2)矛盾. 這樣,就找到了開集GA?A,開集GB?B,滿足GA∩GB=?,所以A,B是隔離的. 設(shè)集合A,B?n,已知A∪B可測(大前提),現(xiàn)在在不同條件下研究A,B各自的可測性. 此時,A,B各自的可測性是無法確定的,有4種可能的情況,即(A的可測性,B的可測性)為(可測,可測)或(可測,不可測)或(不可測,可測)或(不可測,不可測).可以舉例說明. 不妨取A∪B=[0,3].設(shè)S1是[0,1]上的不可測集,S2是[2,3]上的不可測集.下面給出每種A,B不同的可測性組合下A,B的一種可能取值. (可測,可測):A=[2,3],B=[0,2]; (可測,不可測):A=[0,3],B=S2∪[0,1]; (不可測,可測):A=S1∪[2,3],B=[0,3]; (不可測,不可測):A=S1∪[2,3],B=S2∪[0,2]. 此時,A,B的可測性一定是相同的.不然A,B一個可測,另一個不可測.不妨設(shè)A可測,B不可測.由于A∩B=?,且A及A∪B可測,有B=(A∪B)A可測,這便與B不可測矛盾了.所以此時只有兩種情況,即(A的可測性,B的可測性)為(可測,可測)或(不可測,不可測).可以舉例說明. 不妨取A∪B=[0,3].設(shè)S是[0,1]上的不可測集.下面給出每種A,B不同的可測性組合下A,B的一種可能取值. (可測,可測):A=[2,3],B=[0,2);A∩B=?; (不可測,不可測):A=S,B=[0,3]S;A∩B=?. 由3.1和3.2可以發(fā)現(xiàn),在加上一些限制條件之后,A,B的可測性組合也隨之更確定.不過即使在A∩B=?的條件下,也無法由A∪B可測得到A,B均可測.這說明條件“A∩B=?”有一點(diǎn)弱.根據(jù)定理1,下面試試一個更強(qiáng)的條件. 此時,A,B均可測,下面給出證明. 定理2若A?n不可測,則對?B?n,只要A,B是隔離的,那么A∪B不可測. 證假設(shè)A∪B可測,則對?ε>0,?開集G?A∪B,使得m*(G(A∪B))<ε. 因?yàn)锳,B是隔離的,所以?開集VA?A,VB?B,滿足VA∩VB=?.令 GA=VA∩G,GB=VB∩G, 則有 GAA?(GAA)∪(GBB)?G(A∪B), 所以 m*(GAA)≤m*(G(A∪B))<ε. 這說明A可測,與題設(shè)矛盾.故假設(shè)不成立,即A∪B不可測. 推論1若A∪B可測,且A,B是隔離的,那么A,B均可測. 至此,在A∪B可測的大前提下,得到如下A,B均可測的充分條件:A,B是隔離的.不過在A∪B可測的大前提下,即使A,B均可測,A,B也不一定是隔離的.例子很容易找到.例如,A∪B=[0,3],A=[0,3],B=[1,2]. 這就是說,在A∪B可測的大前提下,“A,B是隔離的”只是“A,B均可測”的充分不必要條件,換句話說,這個條件太強(qiáng)了,那么能否找到一個更弱的條件呢? 為找到充要條件,需要逐步減弱條件.由定理1知,“A,B是隔離的”可以轉(zhuǎn)換成“A∩B=?B∩A=?A∩B=?”三個條件.因?yàn)锳∩B=?是很好的性質(zhì),所以選擇先保留這個條件,減弱其他兩個條件.那么減弱之后?B∩A和?A∩B中應(yīng)至少有一個不為空集,而這就成為隔離條件失效的關(guān)鍵因素.于是提出如下猜想: 猜想1設(shè)A∪B可測,A∩B=?,?B∩A和?A∩B均可測.將他們分別從A,B上去掉后,如果剩下的兩個集合滿足隔離條件,那么A,B均可測. 驗(yàn)證猜想1的第一步是從A,B上分別去掉各自的一個可測子集,并保證剩下兩個集合滿足隔離條件,檢驗(yàn)此時A,B是否均可測. 定理3設(shè)A∪B可測,A∩B=?,A*,B*分別是A,B的可測子集,若AA*,BB*是隔離的,則A,B均可測. 證由A∩B=?及A*,B*分別是A,B的子集可得 (A∪B)A*B*=(AA*)∪(BB*). 因?yàn)锳∪B,A*及B*均可測,所以 (AA*)∪(BB*)=(A∪B)A*B* 可測.又因?yàn)锳A*,BB*是隔離,由推論1知,AA*,BB*均可測,所以A=(AA*)∪A*可測.同理,B可測. 接下來證明兩個輔助結(jié)論. 引理1設(shè)集合B?A?n,若AB??A,則?B??A. 證任取x∈?B,要證:x∈?A,只需證:對?ε>0,N(x,ε)∩A≠?且N(x,ε)∩Ac≠?. 現(xiàn)任取ε>0,因?yàn)閤∈?B,所以?y∈N(x,ε)∩B,?z∈N(x,ε)∩Bc?Bc.于是y∈N(x,ε)∩B?N(x,ε)∩A,這說明N(x,ε)∩A≠?. 下證:N(x,ε)∩Ac≠?.分兩類討論. (i)z∈AB. 因?yàn)閦∈AB??A,所以對于ε′=ε-ρ(x,z)>0, ?z′∈N(z,ε′)∩Ac?Ac,由于 ρ(z′,x)≤ρ(x,z)+ρ(z′,z)<ρ(x,z)+ε-ρ(x,z)=ε, 故z′∈N(x,ε),從而z′∈N(x,ε)∩Ac,所以N(x,ε)∩Ac≠?. (ii)z?AB. 此時,考慮到z∈Bc,有z?A,所以z∈N(x,ε)∩Ac,于是N(x,ε)∩Ac≠?. 綜上,對上述ε>0,N(x,ε)∩A≠?且N(x,ε)∩Ac≠?,由ε的任意性,得x∈?A.再由x的任意性知,?B??A. 引理2若A∩B=?,則A°∩?B=?. 證假設(shè)A°∩?B≠?,那么?z∈A°∩?B?A°,所以?δ>0,使N(z,δ)?A,從而A∩B?N(z,δ)∩B.又因?yàn)閦∈A°∩?B??B,所以N(z,δ)∩B≠?,從而A∩B≠?,這與題設(shè)中的A∩B=?矛盾,故假設(shè)不成立,即A°∩?B=?. 最后將從A,B上去掉的兩個子集換成具體的?B∩A和?A∩B,再利用以上兩個輔助定理,證明猜想1. 定理4設(shè)A∪B可測,A∩B=?,若A∩?B,B∩?A均可測,則A,B均可測. 證記A*∶=A∩?B,B*∶=B∩?A,則A*,B*分別是A,B的可測子集.由A∩B=?及引理2知,A°∩?B=?,于是 A*=A∩?B?(A°∩?B)∪(?A∩?B)=?A∩?B??A, 從而A(AA*)=A*??A,由引理1知,?(AA*)??A. 因?yàn)?/p> (BB*)∩?A=(B?A)∩?A=?, 所以 (BB*)∩?(AA*)?(BB*)∩?A=?, 從而 (BB*)∩?(AA*)=?. 同理,(AA*)∩?(BB*)=?. 又因?yàn)?AA*)∩(BB*)=?,由定理1知,AA*,BB*是隔離的.又因?yàn)锳∪B可測,A∩B=?,A*,B*分別是A,B的可測子集,由定理3知,A,B均可測. 上面的研究一直保留了A∩B=?的條件,現(xiàn)在將這個條件減弱為A∩B可測,并由定理4的啟發(fā)得到了定理5. 定理5A,B均可測的充要條件是A∪B,A∩B,A∩?(BA),(BA)∩?A均可測. 證必要性顯然成立. 充分性.記A*∶=A,B*∶=BA,則A*∪B*=A∪(BA)=A∪B可測;A*∩B*=A∩(BA)=?;A*∩?B*=A∩?(BA)可測;B*∩?A*=(BA)∩?A可測,由定理4知,A*,B*均可測,所以A=A*可測,B=(B∩A)∪(BA)=(A∩B)∪B*可測. 推論2若A∪B可測,則A,B均可測的充要條件是A∩B,A∩?(BA),(BA)∩?A均可測. 至此,得到了在A∪B可測的大前提下,A,B均可測的充要條件. 定理5給出了A,B均可測條件的一種等價刻畫.它還有另一個版本:A,B均可測的充要條件是A∪B,A∩B,A∩(BA)′,(BA)∩A′均可測,其中A′表示集合A的導(dǎo)集. 下面給出定理5的一些應(yīng)用. 例1設(shè)S1是[0,1]上的任意一個不可測集合,S2=[0,1]S1,求證:S1∩S′2和S2∩S′1至少有一個不可測. 證假設(shè)S1∩S′2和S2∩S′1均可測.因?yàn)镾1∪S2=[0,1]可測,且S1∩S2=?可測,由定理5知,S1,S2均可測,這與題設(shè)矛盾,故假設(shè)不成立,即S1∩S′2和S2∩S′1至少有一個不可測. 在本例中,由于S1和S2都是抽象的集合,從正面證明十分困難,不過通過反證法,可以由定理5很好地解決. 例2定義在可測集E?n上的函數(shù)f(x)滿足:?x,y∈E,若‖x‖≤‖y‖,則f(x)≤f(y),其中,求證:f(x)是E上的可測函數(shù). 證任取a∈,記 下面分兩類討論. 故 文中給出了兩集合分別可測的另一種等價刻畫,這個刻畫可以使我們更清楚地看到 “A,B均可測”是比“A∪B可測”要強(qiáng)得多的條件,在一般情況下,后者的成立是無法保證前者的成立的.這也否定了一開始的猜測,即“(廣義實(shí)值)函數(shù)f(x)滿足:?a,b∈,E={x∈n;a≤f(x)≤b}是可測的”和“(廣義實(shí)值)函數(shù)f(x)滿足:?a∈,E={x∈n;f(x)≥a}是可測的”兩者是不等價的. 致謝作者非常感謝西北工業(yè)大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院李文娟副教授的有益討論,同時感謝相關(guān)文獻(xiàn)對本文的啟發(fā)以及審稿專家提出的寶貴意見.2 預(yù)備知識
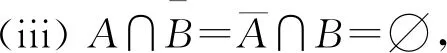
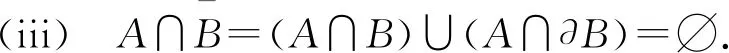
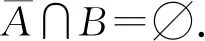
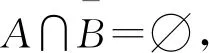

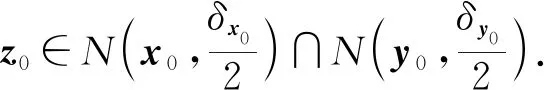
3 主要結(jié)果
3.1 無附加條件
3.2 加上限制條件:A∩B=?
3.3 加上限制條件:A,B是隔離的
3.4 探尋充要條件
4 應(yīng) 用
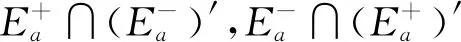
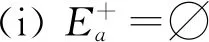

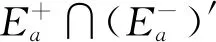
5 結(jié) 論

