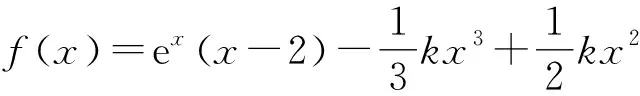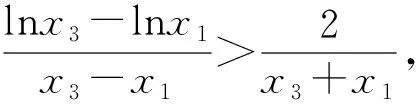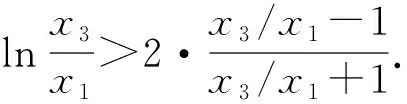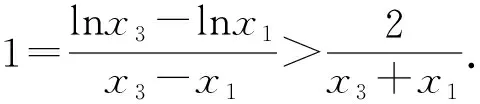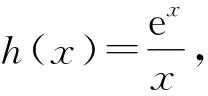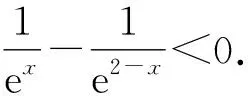妙探“雙變量極值點偏移不等式證明”問題
廖 晗 周 科
(武漢經濟技術開發(fā)區(qū)漢陽三中,湖北 武漢 430109)
破解雙變量極值點偏移不等式證明問題的關鍵:一是轉化,即由已知條件入手,尋找雙參所滿足的關系式,并把含雙參的不等式轉化為含單參的不等式;二是巧構造函數,再借用導數,判斷函數的單調性,從而求其最值;三是回歸雙參的不等式證明,把所求的最值應用到雙參不等式,即可證得結果.
1 真題重現
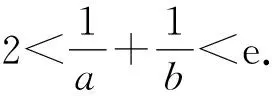
學生解決這道真題主要有三種方法,展示如下:
解法1 將blna-alnb=a-b變形為
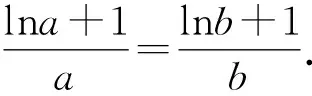

令f(x)=x(1-lnx),則f(m)=f(n),不妨設m
要證m+n>2?n>2-m?f(n) 令g(x)=f(x)-f(2-x),x∈(0,1), 則g′(x)=-lnx-ln(2-x)=-ln[x(2-x)]≥-ln1=0.所以g(x)在區(qū)間(0,1)內單調遞增,所以g(x) 由m(1-lnm)=n(1-lnn), 得m(1-lnm)=tm[1-ln(tm)], 所以h(s)在區(qū)間(0,+∞)內單調遞減. 所以h(s) 所以g(s)在區(qū)間(0,+∞)內單調遞減. 由t∈(1,+∞),得t-1∈(0,+∞). 因為m(1-lnm)=n·(1-lnn)>m,所以要證m+n 令h(x)=x(1-lnx)+x,x∈(1,e),所以h′(x)=1-lnx>0.故h(x)在區(qū)間(1,e)內單調遞增.所以h(x) 由f(x)的單調性易得,0 所以φ(x)>φ(e)=0,h′(x)>0,h(x)在區(qū)間(0,e)內單調遞增. 又因為f(x1)=f(x2), 即(x1-x2)(x1+x2-e)>0. 解法1 由題知f′(x)=ex(x-2)+ex-kx2+kx=(ex-kx)(x-1),因為f(x)有三個極值點,所以方程ex-kx=0有兩個不等根,且都不是1. 令g(x)=ex-kx,當k≤0時,g(x)單調遞增,g(x)=0至多有一根,所以k>0.由g′(x)>0,得x>lnk,由g′(x)<0,得x 所以g(lnk)=elnk-klnk=k(1-lnk)<0,k>e. 此時,g(0)=1>0,lnk>1,g(1)=e-k<0,x→+∞時g(x)→+∞. 所以k>e時,f′(x)=0有三個根x1,x2,x3,且0 由ex1=kx1,得x1=lnk+lnx1. 由ex3=kx3,得x3=lnk+lnx3. 所以φ(t)在(1,+∞)上單調遞增. 所以φ(t)>φ(1)=0. 所以x3+x1>2x2. 解法2 由題知f′(x)=(ex-kx)(x-1),因為f(x)有三個極值點,所以方程ex-kx=0有兩個不等實根,且不為1,顯然也不為0. 所以h(x)在(-∞,0)單調遞減,在(0,1)單調遞減,在[1,+∞)單調遞增. 當x→-∞時,h(x)→0;當x→0+時,h(x)→+∞;當x→0-時,h(x)→-∞;當x→+∞時,h(x)→+∞. 要使y=k與y=h(x)有兩個交點,則需k>e.此時f′(x)=0有三個根x1,x2,x3且0 要證x1+x3>2x2=2,即證x3>2-x1>1.因為h(x)在(1,+∞)單調遞增,故要證:h(x3)>h(2-x1). 因為h(x1)=h(x3),即要證:h(x1)>h(2-x1). 令φ(x)=h(x)-h(2-x),即要證:當0 因為0 所以當0 要證:x1+x3>2x2=2,即證:1>x1>2-x3. 又因為g(x)在(-∞,1)單調遞增,即證:g(x1)>g(2-x3). 因為g(x1)=g(x3),即證:g(x3)>g(2-x3). 即證:g(x3)-g(2-x3)>0. 令h(x)=g(x)-g(2-x),x>1,則 因為x>1,所以1-x<0,x>1>2-x. 所以h′(x)<0.所以h(x)在(1,+∞)單調遞增. 因為x3>1,所以h(x3)=g(x3)-g(2-x3)>h(1)=0. 故原不等式x3+x1>2x2成立. 面對一題多解的問題,要善于積極地開發(fā)和利用數學教學活動中被動生成的問題[1],它是提升自我教學素質的寶貴資源,通過對這些資源的研究,追根溯源,探究本質,使我們對概念有更準確的認識,對方法有更全面的掌握,對思想有更深刻的體會.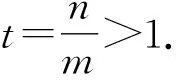
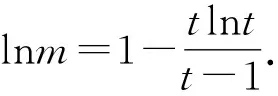
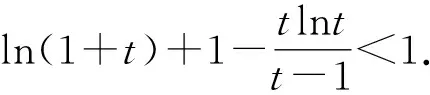
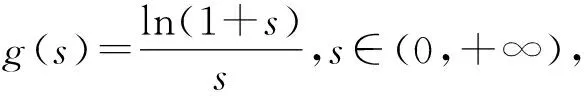
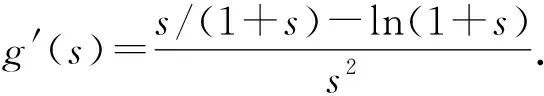
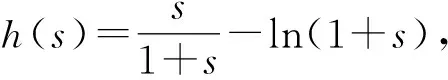


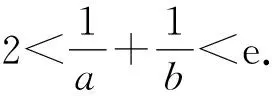

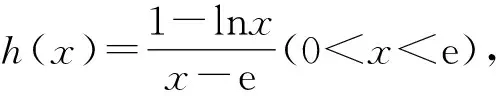




2 變式拓展