王弟成

(江蘇省蘇州實(shí)驗(yàn)中學(xué),江蘇 蘇州 222006)

求直線過定點(diǎn)問題是解析幾何中的常見題型之一,也是高考重點(diǎn)考查的內(nèi)容,因此解決它需要綜合運(yùn)用解析幾何知識(shí),同時(shí)還要注意解題策略的運(yùn)用.

(1)求橢圓C的標(biāo)準(zhǔn)方程;

(2)斜率不為0的直線l與C交于M,N兩點(diǎn),若直線BM的斜率是直線AN斜率的兩倍,證明:直線l經(jīng)過定點(diǎn),并求出其定點(diǎn)坐標(biāo).

1 設(shè)且求,選擇斜率k表示出相應(yīng)直線方程

策略1 從已知條件出發(fā),選擇直線AN的斜率k表示點(diǎn)M,N的坐標(biāo),進(jìn)而表示出直線l的方程,從直線方程中挖掘出定點(diǎn).

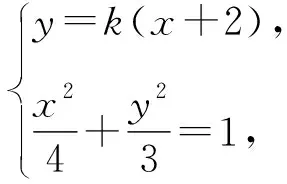
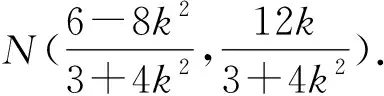
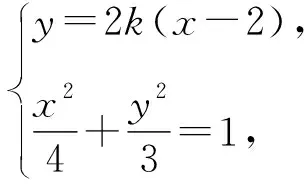
(3+16k2)x2-64k2x+64k2-12=0.

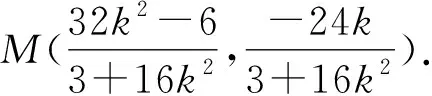
所以直線l的方程為

2 先猜后證,減少運(yùn)算

策略2先利用特殊情況猜想出直線所過的定點(diǎn),再利用斜率或向量證明三點(diǎn)共線,從而得到直線恒過定點(diǎn).

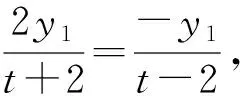
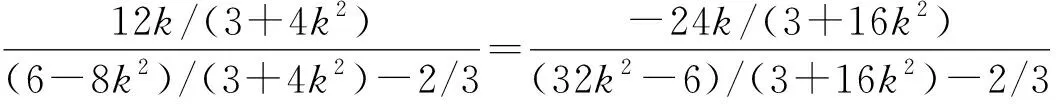
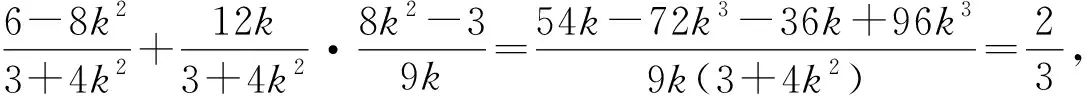
3 設(shè)而不求,整體處理

策略3 上面解法的主要困難在于得到的直線l方程復(fù)雜,不易觀察定點(diǎn).此時(shí)還可以考慮直接設(shè)出直線l方程,根據(jù)條件找到方程中相關(guān)參數(shù)的關(guān)系,此時(shí)再確定定點(diǎn)就很容易.

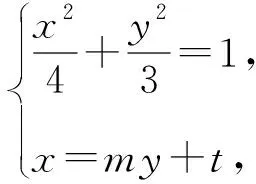
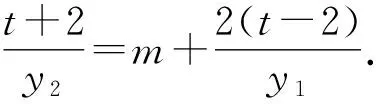
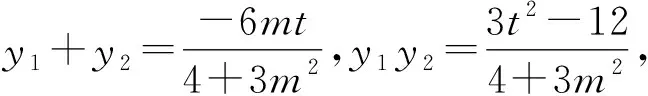
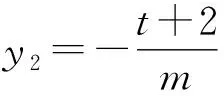
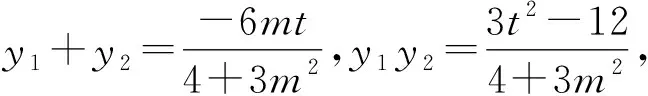
(t+2)y1=my1y2+2(t-2)y2.

即(3t-2)(t+2)y1=(t-2)(3t-2)y2.

4 用性質(zhì)換點(diǎn),尋求對(duì)稱性

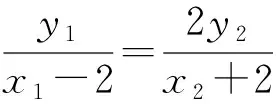
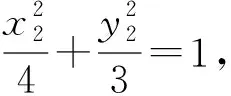
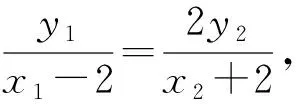
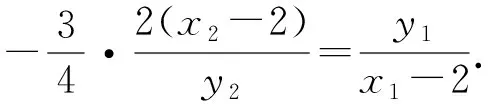
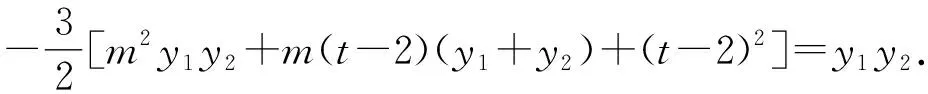
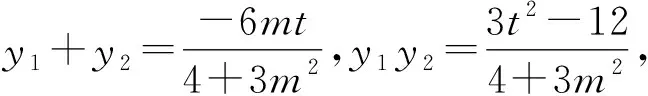
上面的每一種解決方法都有其優(yōu)點(diǎn),解決問題時(shí)需要根據(jù)具體情境,明確方向,識(shí)別模型,選擇模型,確定方法.高三解題理應(yīng)策略優(yōu)先,只有對(duì)各種情況分析透徹,把握本質(zhì),才能在考試中選擇合適的方法解決問題.