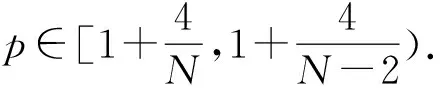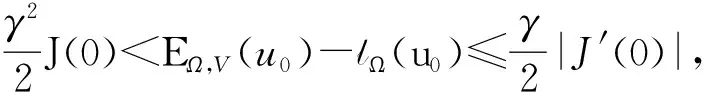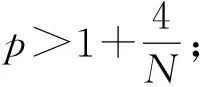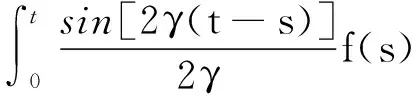一類帶旋轉(zhuǎn)的Gross-Pitaevskii方程
陳咨宇, 張 健
(電子科技大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 四川 成都 611731)
1 研究背景
本文考慮帶旋轉(zhuǎn)的Gross-Pitaevskii方程在部分限制下的柯西問題:
iu
LΩu=0, t≥0, x∈RN,
(1)
u(0,x)=u0(x),
(2)
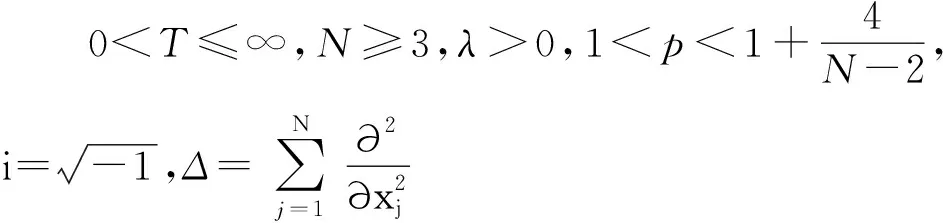
Lz=i(x2?x1-x1?x2),
A=Ω(-x2,x1,0,…,0)∈RN.
刻畫玻色-愛因斯坦凝聚(BEC)的數(shù)學(xué)模型通常被稱為Gross-Pitaevskii方程(簡(jiǎn)稱G-P方程),最早是由Gross[1]和Pitaevskii[2]提出.針對(duì)稀薄原子氣體中BEC的研究,值得注意的超流體特征是量化渦旋[3].目前,從BEC基態(tài)產(chǎn)生量化渦旋的最常用的方法之一是:在控制原子的磁陷阱上施加以角速度旋轉(zhuǎn)的激光束,以產(chǎn)生諧波各項(xiàng)異性的勢(shì)[4-5].根據(jù)平均場(chǎng)理論,當(dāng)溫度T低于臨界溫度Tc時(shí),在旋轉(zhuǎn)框架下的BEC能夠由宏觀的波函數(shù)u(t,x)所刻畫,它的演化由一個(gè)帶角動(dòng)量旋轉(zhuǎn)項(xiàng)的G-P方程控制[6-8].在最新的偶極BEC等宏觀量子現(xiàn)象研究中,外勢(shì)被限制在部分方向上.類似地,本文利用在部分限制下帶旋轉(zhuǎn)的G-P方程模擬此模型.
對(duì)非線性薛定諤方程的研究,引起了眾多數(shù)學(xué)家的關(guān)注.回顧經(jīng)典非線性薛定諤方程
iut+Δu+|u|p-1u=0,t≥0,x∈RN,
(3)

ΔQ-Q+|Q|
Weinstein[13]和Zhang[14]分別得到在L2-臨界與L2-超臨界非線性項(xiàng)爆破解與整體解存在的最佳門檻,證明了此柯西問題爆破解存在的最佳充分條件是
‖u0‖L2<‖Q‖L2.
對(duì)于帶調(diào)和勢(shì)的非線性薛定諤方程
iut+Δu-|x|2u+|u|p-1u=0,
t≥0, x∈RN,
(4)
Oh[15]和Cazenave[16]在相應(yīng)的能量空間中建立了柯西問題(2)和(4)的局部適定性,Tsurumi等[17]和Zhang[18-19]研究了其爆破解的存在性,Zhang[19]得到了其爆破解整體存在的最佳充分條件.
對(duì)于帶部分調(diào)和勢(shì)的非線性薛定諤方程
iu
t≥0, x∈RN, 2≤k≤N-1,
(5)
Antonelli等[20]在相應(yīng)的能量空間內(nèi)建立了柯西問題(2)和(5)的局部適定性以及散射性質(zhì);當(dāng)外勢(shì)限制在部分方向時(shí),Ohta[21]研究了此方程駐波解的不穩(wěn)定性.
Basharat等[22]已經(jīng)對(duì)如下在調(diào)和限制下帶旋轉(zhuǎn)的非線性薛定諤方程做出了研究
iu
t≥0, x∈RN.
(6)
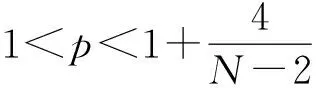
基于以上的研究,通過比較方程(1)和(6),發(fā)現(xiàn)由于限制的作用,使得方程的平移不變性、旋轉(zhuǎn)不變性等不變性缺失,從而導(dǎo)致尺度變換等重要技術(shù)的失效,引起理論研究上的新困難.初步研究顯示,帶限制的非線性薛定諤方程和帶部分限制的2種情形有顯著的差異.典型的是在調(diào)和限制有空間對(duì)稱,而在部分調(diào)和限制情形中空間對(duì)稱性丟失,從而導(dǎo)致在臨界質(zhì)量爆破解的研究上必須尋求新的方法和路徑.
本文主要研究柯西問題(1)和(2)的爆破解存在的充分條件.主要工作如下:通過利用文獻(xiàn)[16]的方法建立了柯西問題(1)和(2)在相應(yīng)的能量空間的局部適定性(也可見文獻(xiàn)[20,31]).根據(jù)文獻(xiàn)[18]的啟示,選擇不帶任何勢(shì)的經(jīng)典非線性薛定諤方程的基態(tài)解刻畫柯西問題(1)和(2)的爆破解,進(jìn)而利用Virial恒等式和Hamilton守恒律可得到柯西問題(1)和(2)的爆破解存在的充分條件.
2 預(yù)備知識(shí)
本節(jié)將給出一些準(zhǔn)備知識(shí).定義能量空間
H={u∈H1(Rdx<∞,
2≤k≤N-1},
其中
H1(RN)={u:u∈L2(RN),▽u∈L2(RN)}.
顯然H是一個(gè)Hilbert空間,賦予其內(nèi)積為
〈φ,ψ〉dx,

為了計(jì)算簡(jiǎn)便,給出以下的命題.
命題 2.11) 由定義可知A=Ω(-x2,x1,0,…,0),則x·A=0.
2) 角動(dòng)量算子Lz=i(x2?x1-x1?x2)是自伴算子,且滿足Lz(|x|2)=0.
3) 定義角動(dòng)量:lΩ(u)=〈LΩu,u〉.
〈L
角動(dòng)量lΩ(u)是實(shí)的.這里內(nèi)積定義為
證明結(jié)論1)和2)顯然.現(xiàn)在僅證明結(jié)論3).
取其共軛,利用分部積分法,有


根據(jù)文獻(xiàn)[16,20,31]給出方程(1)的局部適定性.
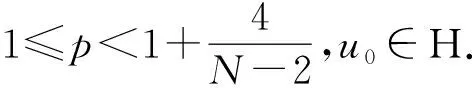
1) 設(shè)u0∈H,則得到柯西問題(1)和(2)一定存在唯一解u(t,x)∈C([0,T*);H),0 2) 對(duì)任意時(shí)間t∈[0,T*),u(t,x)滿足以下的守恒律: 質(zhì)量守恒 (7) 能量守恒 E (8) 角動(dòng)量守恒 lΩ(u)=〈L (9) 為了閱讀方便,我們證明守恒律. 其中l(wèi)Ω(u)=〈LΩu,u〉是實(shí)的,則令 可證得方程(1)質(zhì)量守恒. 其中 (x2?x1-x1?x2)u 因此 則令 E 可證得方程(1)的能量守恒. Re(I1-I2+2I3). 注意有[Δ,Lz]=0,因此由I可知ReI1=0.對(duì)于I2,有 I -γ 對(duì)I2取實(shí)部,有ReI2=0.由于x2?x1-x1?x2是反對(duì)稱的,對(duì)于I3有 I 對(duì)I3取實(shí)部,有 Re(I3)=-pRe(I3)?Re(I3)=0. 結(jié)合I1、I2和I3的結(jié)果,得到 (10) 因此方程(1)的角動(dòng)量守恒. 命題 2.3(Virial等式) 設(shè)u0∈H,且|x|u0∈L2.如果對(duì)應(yīng)的柯西問題(1)和(2)的解u(t,x)其最大存在區(qū)間為[0,T*),則對(duì)任意的t∈[0,T*),u(t,x)∈C([0,T*),H).記 則 (11) 2γ 4EΩ,V-4γ (12) 本節(jié)將利用Virial等式及守恒律討論柯西問題(1)和(2)爆破解存在的充分條件. 由文獻(xiàn)[13],首先給出如下的不等式. 引理 3.1設(shè) u∈∑={u∈H 則 (13) 證明由等式 和Cauchy-Schwarz不等式可得到上述不等式. 這里 則存在0 證明由方程(7)~(9),證明可分為2種情形. J″(t)+4γ 4EΩ,V(u0)-4lΩ(u0). (14) 因此,得 J″(t)+4γ2J(t)= 4EΩ,V(u0)-4lΩ(u0)+4γ 解這個(gè)常微分方程,可得到 lΩ(uds= (15) 這里 f(t)=4γ C>0,β∈(0,π),且 C (16) 條件1)成立時(shí),有 則由C2的表達(dá)式可知,不論EΩ,V(u0)-lΩ(u0)是正還是負(fù),始終有如下關(guān)系式成立 (17) 因此,可知 lΩ(uds, (18) 此時(shí)對(duì)J(t)有 必定存在T使得 由引理3.1中的(13)式以及質(zhì)量守恒可知,存在某個(gè)常數(shù)c0,使得 ‖▽u‖ 因此,此時(shí)柯西問題(1)和(2)的解u(t,x)在有限時(shí)間T*<∞爆破 則(17)式依然成立.后續(xù)證明和以上的步驟相同,必定存在有限時(shí)間T*使得 J″(t)≤4(EΩ,V(u0)-lΩ(u0)). 根據(jù)經(jīng)典的分析恒等式 (19) 有 0≤J(t)≤ J(0)+J′(0)t+2(EΩ,V(u0)-lΩ(u0))t2. 若u0滿足條件3)、4)或5),則必定存在有限時(shí)間T*使得 注 3.1若V=γ2|x|2|u|2是調(diào)和勢(shì)[22],則定理3.1中的條件1)等價(jià)于 EΩ,V(u (20) 即當(dāng)E0,0(u0)≤0時(shí),柯西問題(2)和(6)的解在T*處爆破.然而,當(dāng) V=γ 是部分調(diào)和勢(shì)時(shí),上述條件就不再成立.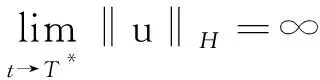


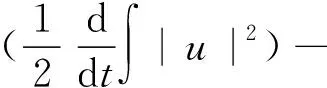

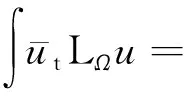
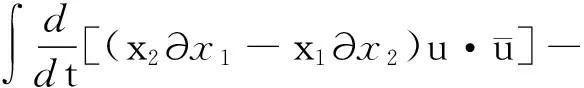

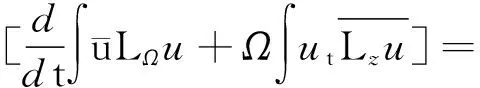

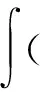

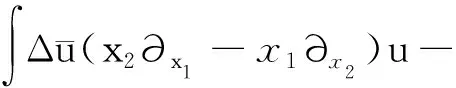

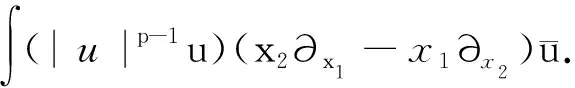

3 帶旋轉(zhuǎn)的G-P方程爆破解的充分條件