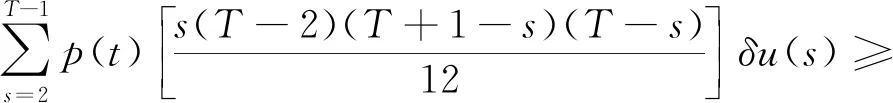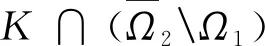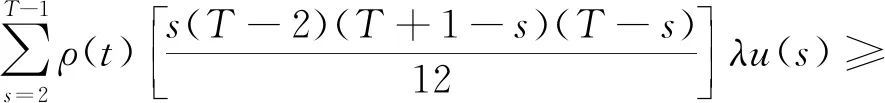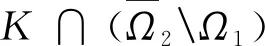趙亞麗,陳天蘭

(西北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,甘肅 蘭州 730070)

令T≥4為一整數(shù).記

T0={0,1,…,T+1},

T1={1,2,…,T},

T2={2,3,…,T-1}.

離散邊值問題由于其重要的理論價(jià)值和物理背景,一直受許多研究者所關(guān)注,并獲得了豐富的研究成果[1-11].眾所周知,彈性梁方程在工程中有著不可或缺的作用,近年來(lái),對(duì)兩端簡(jiǎn)單支撐的非線性四階離散邊值問題解的存在性和多重性研究已有大量結(jié)果[2-3,6-7],其中大多數(shù)結(jié)果是基于錐上的不動(dòng)點(diǎn)定理、不動(dòng)點(diǎn)指數(shù)理論和拓?fù)涠壤碚摰?

He等[3]運(yùn)用錐上的不動(dòng)點(diǎn)定理研究了非線性四階離散邊值問題

Δ4u(t-2) -λa(t)f(u(t))=0,

t∈{2,3,…,T+2},

u(0)=u(T+2)=Δ2u(0)=Δ2u(T)=0

正解的存在性,其中λ是特征值,權(quán)函數(shù)a:{1,2,…,T+1}→[0,∞),f:R+→R+連續(xù)且T≥1.

Ma等[4]運(yùn)用不動(dòng)點(diǎn)指數(shù)理論研究了非線性四階離散邊值問題

Δ4u(t-2)-λf(t,u(t))=0,

t∈{2,3,…,T},

u(1)=u(T+1)=Δ2u(0)=Δ2u(T)=0

正解的存在性和多解性,其中λ>0是參數(shù),f:T2×[0,∞)→[0,∞)連續(xù)且T≥5.然而,關(guān)于非線性四階離散邊值問題

Δ4u(t-2)+f(u(t))=0,t∈T2,

(1)

u(0)=Δu(0)=Δu(T)=Δ2u(0)=0

(2)

正解存在性從未被研究,其中f:[0,∞)→[0,∞)連續(xù).事實(shí)上,在首次建立其相應(yīng)線性問題的格林函數(shù)時(shí)帶來(lái)了極大的挑戰(zhàn)性,進(jìn)而在討論其性質(zhì)時(shí),又是一項(xiàng)非常艱巨的任務(wù),因此,對(duì)該類問題的研究是非常有必要和有意義的.

為此,本文運(yùn)用錐上的不動(dòng)點(diǎn)定理獲得了非線性四階離散問題(1)～(2)正解的存在性.

本文總假定:

(Hf)f:[0,∞)→[0,∞)連續(xù).

記

則f0=0且f∞=∞對(duì)應(yīng)超線性情形,f0=∞且f∞=0對(duì)應(yīng)次線性情形.

本文的主要結(jié)果如下:

定理1假定(Hf)成立且f滿足:

f0=0且f∞=∞.

則問題(1)～(2)至少存在一個(gè)正解.

定理2假定(Hf)成立且f滿足:

f0=∞且f∞=0.

則問題(1)～(2)至少存在一個(gè)正解.

1 預(yù)備知識(shí)

本文使用的主要工具是:

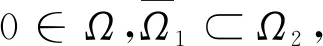
滿足:

(i) ‖Au‖≤‖u‖,u∈K∩?Ω1且‖Au‖≥‖u‖,u∈K∩?Ω2或

(ii) ‖Au‖≥‖u‖,u∈K∩?Ω1且‖Au‖≤‖u‖,u∈K∩?Ω2,

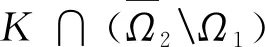
引理2設(shè)h:T2→R.則四階線性邊值問題

Δ4u(t-2)+h(t)=0,t∈T2,

u(0)=Δu(0)=Δu(T)=Δ2u(0)=0

(3)

等價(jià)于

(4)

其中

證明設(shè)u滿足式(3),則通過對(duì)式(3)中的方程進(jìn)行一系列和分運(yùn)算,結(jié)合u(0)=Δu(0)=Δ2u(0)=0可得,

(5)

代入邊界條件Δu(T)=0,有

進(jìn)而解得

(6)

將式(6)代入式(5)中可得,

T(T-1)(t-s)(t-s-1)(t-s+1)]·

[6T(T-1)]-1h(s)+

因此,u也滿足式(4).

另一方面,很容易驗(yàn)證式(4)滿足式(3).

引理3格林函數(shù)G(t,s)滿足如下性質(zhì):

(i)G(t,s)≥0,s,t∈T1.

(ii)ρ(t)Φ(s)≤G(t,s)≤Φ(s),s,t∈T1.其中

證明(i) 當(dāng)1≤t≤s≤T-1時(shí),顯然,G(t,s)≥0.

當(dāng)2≤s≤t≤T時(shí),下面分兩種情況討論.當(dāng)t-s-1≤0時(shí),顯然G(t,s)≥0;當(dāng)t-s-1>0時(shí),即t>s+1,有

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

1)]-1>{(t-3)[t(t-1)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s+1)]}[6T(T-1)]-1=

{(t-3)[(t2-t)(T2-2Ts+s2+T-s)-

(T2-T)(t2-2ts+s2+t-s)]}[6T(T-1)]-1=

{(t-3)[s2(t2-T2)+s2(T-t)+2stT(T-t)+

s(T2-t2)+s(t-T)+2tT(t-T)]}[6T(T-

1)]-1={(t-3)(T-t)[s2(1-T-t)+

s(2tT+T+t-1)-2tT]}[6T(T-1)]-1=

{(t-3)(s-1)(T-t)[2tT-s(T+t-1)]}

[6T(T-1)]-1>{(t-3)(s-1)(T-t)[2(s+

1)T-sT-st+s]}[6T(T-1)]-1=

{(t-3)(s-1)(T-t)[s(T-t)+2T+s]}

[6T(T-1)]-1≥0.

(7)

故(i)成立.

(ii) 當(dāng)1≤t≤s≤T-1時(shí),有

另一方面,

當(dāng)2≤s≤t≤T時(shí),有

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

另一方面,同式(7)的處理方法,則

G(t,s)=[t(t-1)(t-2)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s-1)(t-s+1)][6T(T-

1)]-1>{(t-2)[t(t-1)(T+1-s)(T-s)-

T(T-1)(t-s)(t-s+1)]}[6T(T-1)]-1=

{(t-2)(s-1)(T-t)[2tT-s(T+t-1)]}·

[6T(T-1)]-1≥

[(t-2)(T-t)(T-t+1)s(T-2)(T+1-

s)(T-s)][12T(T-1)3(T-3)]-1.

故(ii)成立.

引理4設(shè)h:T2→[0,∞).則問題(3)的唯一解u非負(fù),且滿足

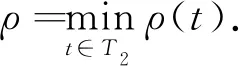
證明由引理2和引理3可知,u(t)非負(fù),且對(duì)任意t∈T1,有

進(jìn)而得到,

另一方面,

ρ(t)‖u‖≥ρ‖u‖.

下面引入本文使用的空間:

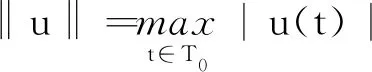
定義非線性算子A:K→E,

依據(jù)引理2,很容易得到如下結(jié)論成立.

引理5若(Hf)成立,則u(t)是問題(1)～(2)的正解當(dāng)且僅當(dāng)Au=u.

引理6若(Hf)成立,則算子A:K→K全連續(xù)且A(K)?K.

證明由引理4可知,A(K)?K.由Arzel-Ascoli定理可知,A:K→K是全連續(xù)的.

2 主要結(jié)果的證明

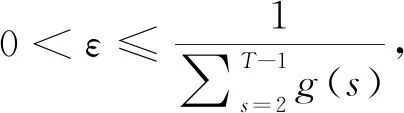
Ω1={u∈E:‖u‖

則對(duì)任意u∈K∩?Ω1,t∈T1,由引理3可得,

(8)

其中

因此,

‖Au‖≤‖u‖,u∈K∩?Ω1.

Ω2={u∈E:‖u‖

則對(duì)任意u∈K∩?Ω2,t∈T2,由引理4可得,

由引理3和引理4可得,

因此,

‖Au‖≥‖u‖,u∈K∩?Ω2.

Ω1={u∈E:‖u‖

則對(duì)任意u∈K∩?Ω1,t∈T2,由引理3和引理4可得,

‖u‖.

因此,

‖Au‖≥‖u‖,u∈K∩?Ω1.

下面分兩種情況考慮.

(i) 若f有界.即存在L>0,對(duì)任意u∈[0,∞),有f(u)≤L.記

Ω2={u∈E:‖u‖

則對(duì)任意u∈K∩?Ω2,t∈T1,由式(8)可得,

因此,

‖Au‖≤‖u‖,u∈K∩?Ω2.

若u∈K∩?Ω2,則有f(u)≤ηH2.由式(8)可得,

因此,

‖Au‖≤‖u‖,u∈K∩?Ω2.