陳寒霜,龍見仁,王 玲

(貴州師范大學數(shù)學科學學院,貴州 貴安新區(qū) 550025)

1 引言和主要結果

設C為復平面,f為C上的亞純函數(shù),本文假定讀者熟悉Nevanlinna值分布理論的標準記號和基本結論,具體可參考文獻[1-2].例如,m(r,f),N(r,f),T(r,f)分別表示f的均值函數(shù)、計數(shù)函數(shù)以及特征函數(shù).假設a(z)和f(z)為亞純函數(shù),若滿足

T(r,a)=o(T(r,f)),r→∞,

那么稱a(z)為f(z)的一個小函數(shù).亞純函數(shù)f(z)的增長級用ρ(f)來表示,定義如下:

1637年,法國數(shù)學家費馬提出了著名的“費馬大定理”,他斷言當正整數(shù)n>2時,關于x,y,z的方程xn+yn=zn沒有非平凡正整數(shù)解.歷經(jīng)三百多年,最終被英國數(shù)學家Wiles[3]論證了該結論的正確性.而方程

f(z)n+g(z)n=1

(1)

則被視為費馬方程的函數(shù)形式,其中n是一個正整數(shù).Gross[4]證明了n≥4時,方程(1)沒有超越亞純函數(shù)解.Montel[5]證明了n≥3時方程不存在超越整函數(shù)解.當n=2時,Gross[6]在1966年得到方程的整函數(shù)解的形式必為f(z)=sin(h(z))和g(z)=cos(h(z)),其中h(z)是一個整函數(shù).

1970年Yang[7]考慮了一般化的費馬型函數(shù)方程

f(z)n+g(z)m=1,

(2)

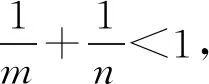
f′(z)n+f(z+c)m=1,

(3)

f′(z)n+(Δcf(z))m=1,

(4)

其中m和n為正整數(shù),并證明了以下的結論.

定理1[8]如果m≠n,則方程(3)沒有有窮級超越整函數(shù)解.

定理2[8]如果m≠n,且m>1,n>1,則方程(4)沒有有窮級超越整函數(shù)解.

于是,結合Yang[7]的結論一個自然的問題是考慮在m=n=2情況下,方程(3)對應的微分-差分方程解的精確形式.2012年Liu等[8]繼續(xù)考慮了這個問題,并得到下面的結論.

定理3[8]方程

f′(z)2+f(z+c)2=1

(5)

的有窮超越整函數(shù)解的形式一定滿足f(z)=sin(z±Bi),其中B是常數(shù),c=2kπ或c=2kπ+π(k∈Z).

定理3表明當m=n=2時,方程(5)存在超越整函數(shù)解,且解的增長級為1.因此,學者們進一步考慮微分-差分方程整函數(shù)解的性質(zhì).2013年Liu等[9]證明了方程(6)和(7)的超越整函數(shù)解的級至少為1,

f(z)2+f′(z)f(z+c)=1,

(6)

f′(z)2+f(z)f(z+c)=1.

(7)

應用類似的證明方法,秦大專[10]證明方程(8)和(9)的超越整函數(shù)解的級至少為1,

f(z)2+f(k)(z)f(z+c)=1,

(8)

(f(k)(z))2+f(z)f(z+c)=1.

(9)

秦大專[10]同時還考慮了下面3個方程整函數(shù)解的增長性.

f(z)2+f(z)Δcf(z)=1,

(10)

f(z+c)2+f(z)Δcf(z)=1,

(11)

f′(z)2+f(z)Δcf(z)=1.

(12)

定理4[10]方程(10)～(12)的超越整函數(shù)解的級至少是1.

受文獻[9-10]的啟發(fā),考慮了下列方程超越整函數(shù)解的增長性,并得到下面的定理.

f(z+c)2+f(k)(z)f(z)=1,

(13)

f(k)(z)2+f(z)Δcf(z)=1,

(14)

f(z)2+f(k)(z)Δcf(z)=1.

(15)

定理5方程(13)～(15)的超越整函數(shù)解的級至少是1.

在上述結論的基礎上,本文接著討論方程(13)的一般化情行,即

f(z+c)n+f(k)(z)f(z)=1.

(16)

定理6當n=1或n≥3時,方程(16)沒有有窮級超越整函數(shù)解.

對于一些費馬型微分-差分方程,已經(jīng)得到了諸多結果,具體可看參考文獻[8-9,11-12],本文在文獻[13]的研究基礎上,考慮復微分-差分方程解的存在性.

2021年Chen等[14]則考慮了兩類較為復雜的費馬型微分-差分方程(17)和(18),得到了相應的結果.

(f(z)f′(z))n+P(z)2f(z+η)m=Q(z),

(17)

(f(z)f′(z))n+P(z)(Δηf(z))m=Q(z).

(18)

定理7[14]如果m=n,則方程(17)沒有有窮級超越整函數(shù)解,其中P(z)和Q(z)為非零多項式,m和n為正整數(shù),且η∈C{0}.

定理8[14]如果m≠n,n>2,則方程(18)沒有有窮級超越整函數(shù)解,其中P(z)和Q(z)為非零多項式,m和n為正整數(shù),且η∈C{0}.

受定理7和定理8的啟發(fā),本文進一步考慮它們的高階導數(shù)形式,即

(f(z)f(k)(z))n+P(z)2f(z+η)m=Q(z),

(19)

(f(z)f(k)(z))n+P(z)(Δηf(z))m=Q(z),

(20)

并得到下面的結論.

定理9如果m=n,則方程(19)沒有有窮級超越整函數(shù)解,其中P(z)和Q(z)為非零多項式,m和n為正整數(shù),且η∈C0}.

定理10如果m≠n,n>2,則方程(20)沒有有窮級超越整函數(shù)解,其中P(z)和Q(z)為非零多項式,m和n為正整數(shù),且η∈C0}.

2 引 理

為證明所給出的定理,下面介紹幾個輔助結果.首先介紹差分版本的Clunie引理.

引理1[15]設f(z)是方程

fn(z)P(z,f)=Q(z,f)

的超越亞純函數(shù)解,其中P(z,f)和Q(z,f)是關于f的差分多項式,令δ<1,ε> 0,若degQ(z,f)≤n,對所有|z|=r?E,有

o(T(r,f))

其中E是對數(shù)測度有窮的集合.

為了處理方程中Δcf(z)這一項,需要用到文獻[16]中的引理3.5,使得f(z)和平移差分f(z+c)與f′(z)之間產(chǎn)生聯(lián)系.

引理2[16]設f是級為p(f)(<1)的超越亞純函數(shù),令h>0,則存在一個ε-集E,使得當z→∞(z∈CE),|c|≤h時,

f(z+c)-f(z)=cf′(z)(1+o(1))

是一致的.

下面介紹有窮級亞純函數(shù)f(z)和f(z+c)特征函數(shù)的關系.

引理3[17]設f是一個級為p(f)(<∞)的超越亞純函數(shù),則對于任意給定的ε>0,

T(r,f(z+c))=T(r,f)+O(rp(f )-1+ε)+O(logr).

進一步地,若ρ(f)<1,則

T(r,f(z+c))=T(r,f)+S(r,f).

下面給出整函數(shù)的哈達瑪分解定理.

引理4[18]設f是一個級ρ(f)(<∞)的整函數(shù),z=0為其k重零點,z1,z2,…為f的非零零點,則

f(z)=zkP(z)eQ(z),

其中P(z)為f的非零零點的典型乘積,Q(z)為次數(shù)不高于ρ(f)的多項式.

Wiman-Valiron定理常常被應用于研究微分方程解的性質(zhì),下面介紹Wiman-Valiron定理.

其中v(r)是f的中心指標,m≥0且r?F.

下面的引理將用于證明方程(21)沒有超越整函數(shù)解.

引理6[18]設fj(z)為亞純函數(shù),gj(z)為整函數(shù),滿足下列條件:

(ii) 當1≤j

(iii) 當1≤j≤n,1≤h

T(r,fj)=o(T(r,egh-gk))(r→∞,r?E),

E為一個線性測度有窮的集合.則

fj≡0.

Halburd等[19]和Chiang等[17]分別獨立地給出了差分版本的對數(shù)導數(shù)引理.下面僅介紹本文證明所需形式.

引理7[17]設f是一個級為ρ(f)(<∞)的超越亞純函數(shù),則對于任意給定的ε>0,有

3 定理5和定理6的證明

定理5的證明先證明方程(13)的超越整函數(shù)解的級至少是1.假設結論不成立,即方程(13)存在一個級ρ(f)<1的超越整函數(shù)解f,下面將導出矛盾.事實上,可由引理2知,存在一個ε-集E1,使得當z?E1,且z→∞時,有

所以有

(21)

再由引理5知,存在一個對數(shù)測度有窮的集合E2?(1,∞)使得對所有的|z|=r?E2和|f(z)|=M(r,f)的z有

(22)

設E3={|z|:z∈E1},則E3的對數(shù)測度有窮.由方程(21)和(22)可知,對所有滿足|z|?[0,1]∪E2∪E3和|f(z)|=M(r,f)的z有

(23)

由于f是超越整函數(shù),并且

所以當z→∞時,

(24)

由式(23),(24)導出式(23)左邊趨于0,顯然這是矛盾的,因此方程(13)超越整函數(shù)解的級至少是1.使用類似前面的證明方法可證方程(14)和(15)超越整函數(shù)解的級至少為1,定理5證畢.

定理6的證明假設f是方程(16)的一個有窮級超越整函數(shù)解.下面導出矛盾.當n=1時,由方程(18)有

f(z)f(k)(z)=1-f(z+c).

根據(jù)引理2得

m(r,f(k)(z))=S(r,f).

顯然這是不可能的.而當n≥3的情況則由Yang在文獻[7]中的結論就能說明此時方程(16)不存在超越整函數(shù)解,故定理6得證.

4 定理9和定理10的證明

定理9的證明假設f是方程(19)的一個有窮級超越整函數(shù)解,下面分3種情況討論:

情形1:m=n=1,那么方程(19)可改寫成

f(z)f(k)(z)+P(z)2f(z+η)=Q(z),

即

f(z)f(k)(z)=Q(z)-P(z)2f(z+η).

由Clunie引理有

m(r,f(k))=S(r,f).

因此

T(r,f(k))=m(r,f(k))=S(r,f).

顯然這是不可能的,即此定理結論成立.

情形2:m=n=2,那么方程(19)可寫成下面的形式

(f(z)f(k)(z))2+P(z)2f(z+η)2=Q(z).

(25)

因此,方程(25)改寫成

(26)

由方程(26)知f(z)f(k)(z)+iP(z)f(z+η)和f(z)f(k)(z)-iP(z)f(z+η)有有窮個多個零點,結合方程(25)和哈達瑪分解定理有

f(z)f(k)(z)+iP(z)f(z+η)=Q1eh(z)

和

f(z)f(k)(z)-iP(z)f(z+η)=Q2e-h(z),

其中h(z)為非常數(shù)多項式,Q1,Q2是非零多項式,且Q1Q2=Q(z),因此,

(27)

(28)

對方程(28)求k階導,有

其中

Mt(h(t),h(t-1),…,h′)]P(h)Pk-1-

Mt(h(t),h(t-1),…,h′)]P(k-h)Pk-1+o(h1(z)),

Nt(h(t),h(t-1),…,h′)]P(h)Pk-1-

Nt(h(t),h(t-1),…,h′)]P(k-h)Pk-1+o(h2(z)).

Mt和Nt是關于(h(t),h(t-1),…,h′,h)的微分多項式.再結合f(z)f(k)(z)和f(z+η)f(k)(z+η)的表達式,有

f(z+η)f(k)(z+η)=

(29)

其中r1,r2,r3分別記成以下的形式:

r1(z)=h1(z)Q1(z),

r2(z)=h1(z)Q2(z)+h2(z)Q1(z),

r3(z)=h2(z)Q2(z).

因此由方程(29)有

r1(z)e2h(z)+h(z+η)-r2(z)eh(z+η)+r3eh(z+η)-2h(z)+

2Pk+2(z)Q1(z+η)e2h(z+η)+

2Pk+2(z)Q2(z+η)≡0.

記

deg(2h(z))=deg(±h(z+η))=

deg(2h(z+η))≥1,

deg(2h(z)-h(z+η))≥1,

deg(2h(z)+h(z+η))≥1,

deg(-2h(z)-h(z+η))≥1.

由引理6有

2Pk+2(z)Q1(z+η)=2Pk+2(z)Q2(z+η).

此與假設P(z),Q1(z),Q2(z)為非零多項式矛盾,因此定理結論成立.

情形3:m=n>2,此時可將方程(19)改寫成

由Yang[7]的結論知上述方程不存在超越整函數(shù)解,定理證畢.

定理10的證明要證明方程(20)在m≠n且n>2時沒有有窮級超越整函數(shù)解,只需要證明下面這個微分-差分方程不存在有窮級超越整函數(shù)解,

[f(z)f(k)(z)]n+P(z)[Δηf(z)]=Q(z).

(30)

現(xiàn)在假設方程(30)有一個超越整函數(shù)解f(z).對方程(30)微分,有

nf(k)(z)n-1[f(z)n-1f′(z)f(k)(z)+

f(z)nf(k+1)(z)]=Q′(z)-P′(z)(Δηf(z))-

P(z)(Δηf′(z)).

(31)

從式(30)中將Δηf(z)表示出,并代入到方程(31)中得到

(32)

P(z)(Δηf′(z)).

注意到n-1≥2,由引理1就有

m(r,φ(z))=S(r,f),m(r,g(z)φ(z))=S(r,f).

此時φ(z)≠0,否則,當φ(z)=0時,f(z)f(k)(z)=C1P(z),C1為非零常數(shù),這顯然與假設是矛盾的.由f是超越整函數(shù)解,有N(r,φ(z))=S(r,f),因此

T(r,g(z))=m(r,g(z))≤m(r,g(z)φ(z))+

S(r,g(z))=S(r,g(z)).

即

T(r,f(k))=T(r,g(z))≤S(r,g(z))=

S(r,f(k)).

這是不可能的,定理10證畢.