無界區(qū)域上一類帶有權(quán)函數(shù)的半線性橢圓方程解的存在性
2023-05-17 05:18:30韓亮謝君輝
韓亮, 謝君輝
( 湖北民族大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 湖北 恩施 445000 )
0 引言
本文研究如下無界區(qū)域上的一類帶有權(quán)函數(shù)的半線性橢圓方程:
(1)
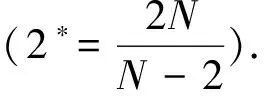
當(dāng)問題(1)中的Ω不包含原點(diǎn)時(shí),問題(1)是帶權(quán)函數(shù)的半線性橢圓方程.文獻(xiàn)[11]的作者用變分原理和山路引理討論了如下無界區(qū)域上的半線性橢圓方程解的存在性:
(2)
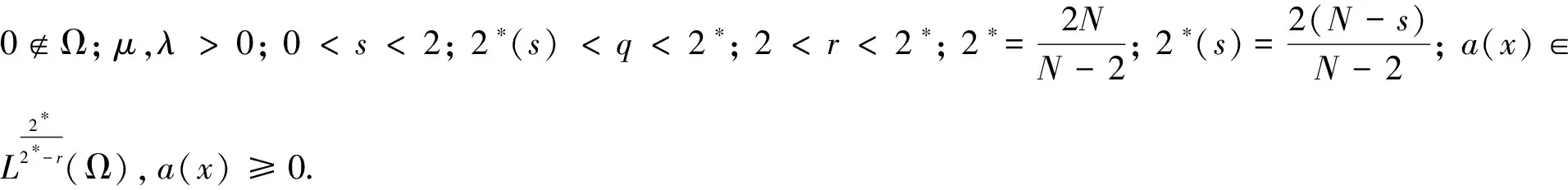
(3)

當(dāng)問題(1)中的Ω為包含原點(diǎn)的區(qū)域時(shí)(系數(shù)有奇性),稱問題(1)是帶有Hardy項(xiàng)的半線性橢圓方程的邊值問題.文獻(xiàn)[13]的作者研究了如下無界區(qū)域上的一類帶Hardy項(xiàng)且具有臨界指數(shù)的半線性橢圓方程非平凡解的存在性:
(4)
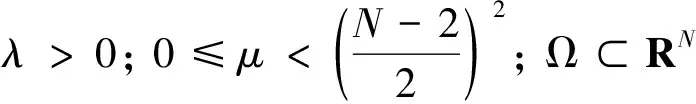
(5)
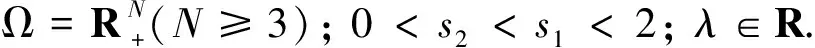
1 預(yù)備知識(shí)
對(duì)任意的u∈H(Ω),問題(1)所對(duì)應(yīng)的能量泛函為:
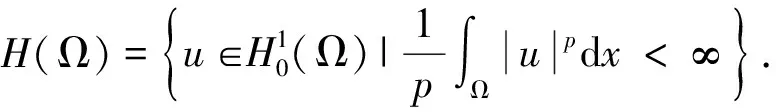
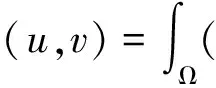
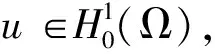

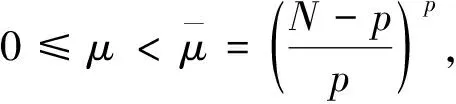
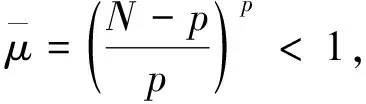
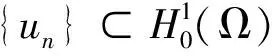
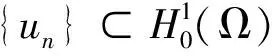
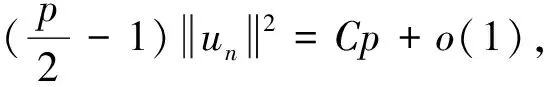
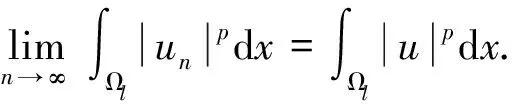
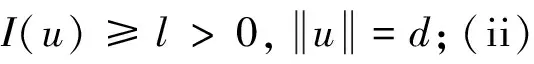
引理5[16](偶泛函臨界點(diǎn)定理)設(shè)E是一個(gè)無限維的Banach空間,偶泛函I∈C1(E,R)滿足PS條件和以下條件:
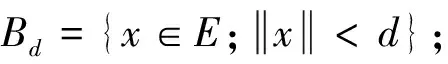
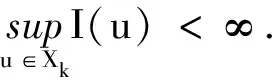
Γm={K?E;K關(guān)于0是緊對(duì)稱的且?h∈Γ1,ψ(K∩h(?B1))≥m}.
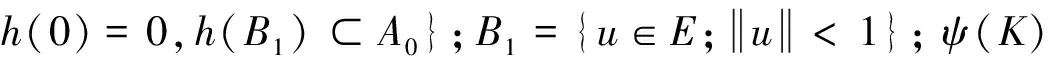
1)當(dāng)0 2)若對(duì)某個(gè)m∈{1,2,…,k}有bm=bm+1成立,則對(duì)于每個(gè)bm,泛函I有無窮多個(gè)臨界點(diǎn).2 主要結(jié)果及其證明
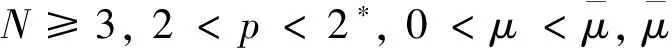
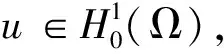
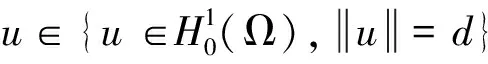
猜你喜歡
科學(xué)技術(shù)創(chuàng)新(2022年33期)2022-11-12 10:21:28
海洋通報(bào)(2022年4期)2022-10-10 07:41:48
數(shù)學(xué)物理學(xué)報(bào)(2022年5期)2022-10-09 08:57:46
數(shù)學(xué)物理學(xué)報(bào)(2021年4期)2021-08-30 08:27:44
傳感器與微系統(tǒng)(2019年8期)2019-08-15 10:59:54
數(shù)學(xué)物理學(xué)報(bào)(2018年1期)2018-03-26 08:16:40
政工學(xué)刊(2017年2期)2017-02-20 09:05:32
思維與智慧·下半月(2016年11期)2016-12-02 17:44:13
中央民族大學(xué)學(xué)報(bào)(自然科學(xué)版)(2015年3期)2015-06-11 02:13:46
中北大學(xué)學(xué)報(bào)(自然科學(xué)版)(2015年3期)2015-03-11 14:04:38

