程春民

(江西省永豐中學)

把一個平面圖形沿某條直線翻折,轉化為空間圖形,進而研究圖形在位置關系和數(shù)量關系上的變化,這就是翻折問題.高考中經(jīng)常以圖形翻折作為命題對象,處理這類問題的關鍵在于弄清楚哪些量發(fā)生了變化,哪些量未發(fā)生變化.本文通過具體例子說明處理這類翻折問題的基本方法.

例1如圖1 所示,四邊形ABCD是菱形,∠BCD＝60°,AB＝2.沿BD把△ABD折起,使點A翻折到點P的位置,連接PC,則四面體P-BCD(如圖2)的體積的最大值是________.

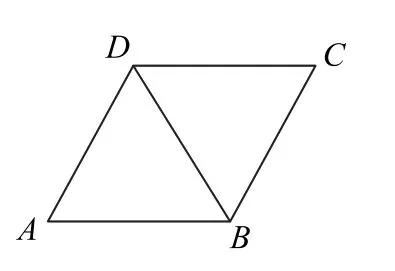
圖1

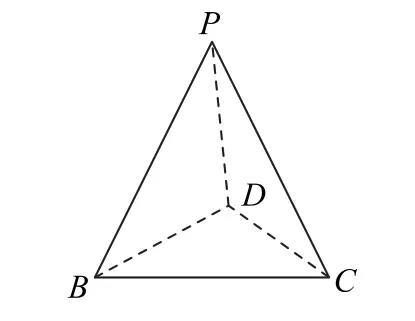
圖2

解析如圖3 所示,當平面PBD⊥平面BCD時,四面體P-BCD的體積最大,過點P作PE⊥BD于點E,則V＝

圖3

例2點D是Rt△ABC斜邊AB上一動點,AC＝3,BC＝4,將△BCD沿著CD翻折,翻折后的三角形為△B′CD,且平面B′CD⊥平面ADC,則翻折后AB′的最小值是( ).

圖4

因為平面B′CD⊥平面ACD,B′E⊥CD,所以B′E⊥平面ACD,故B′E⊥AE.在Rt△AEB′中,由勾股定理得AB′2＝AE2＋B′E2＝25－12sin2α.當時,AB′取得最小值,故選B.

例3如圖5所示,已知四面體ABCD中,AD＝DB＝AC＝CB＝1,則該四面體體積的最大值為________.

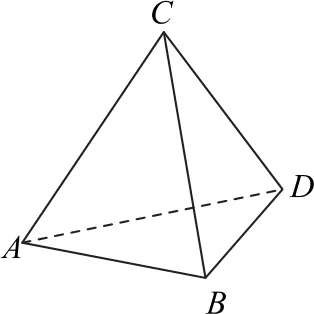
圖5

解析當此四面體體積最大時,平面ABC⊥ABD,取AB中點M,連接CM,DM(如圖6),則CM⊥平面ABD.設AB＝2x(0＜x＜1),則,所以

圖6

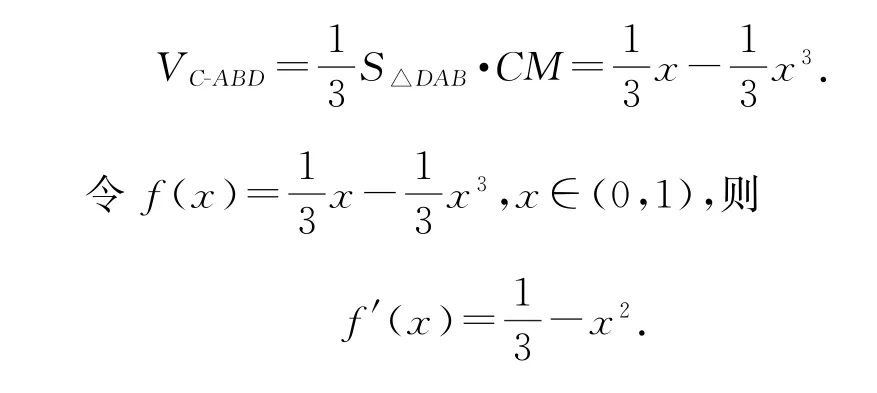
例4如圖7所示,在長方形ABCD中,AB＝2,BC＝1,E為DC的中點,F為線段EC(端點除外)上的一動點,現(xiàn)將△ADF沿AF折起,使平面ABD⊥平面ABC,在平面ABD內過點D作DK⊥AB,K為垂足,設AK＝t,則t的取值范圍是_________.

圖7

解析如圖8 所示,過點D作DH⊥AF,垂足為H,連接HK,因為DK⊥AB,所以AF⊥平面DHK.

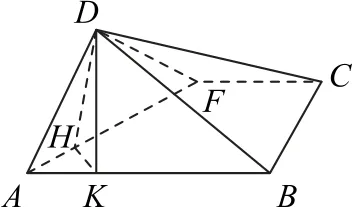
圖8

在平面圖形ABCD中(如圖9),D,H,K三點共線,且DK⊥AF,所 以△AKD≌△DAF,則,所以.又DF∈(1,2),所以

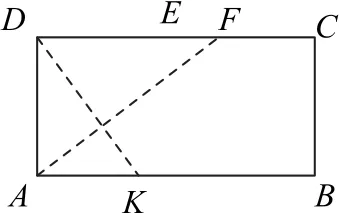
圖9

例5如圖10 所示,在△ABC中,AB＝BC＝2,∠ABC＝120°.若平面ABC外的點P和線段AC上的點D,滿足PD＝DA,PB＝BA,則四面體P-BCD的體積最大值是_________.

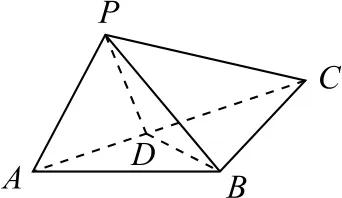
圖10

解析在△ABC中,由余弦定理得

AC2＝BA2＋BC2－2BA·BCcos∠ABC＝12,所以AC＝2.當平面PBD⊥平面CDB時,四面體P-BCD的體積取得最大值.此時△PBD底邊BD的高就是三棱錐VP-BCD的高.

鏈接練習

1.已知邊長為2的等邊△ABC,D為BC的中點,以AD為折痕進行折疊,使折后的∠BDC＝,則過A,B,C,D四點的球的表面積為( ).

A.3π B.4π C.5π D.6π

2.如圖11所示,在正方形SG1G2G3中,E,F分別是G1G2,G2G3的中點,D是EF的中點,現(xiàn)在沿SE,SF及EF把這個正方形折成一個四面體,使G1,G2,G3三點重合,重合后的點記為G,則在四面體S-EFG中必有( ).

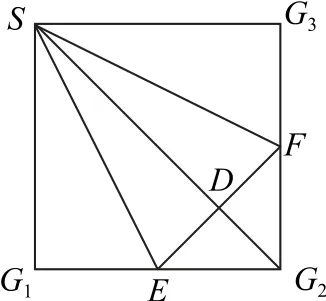
圖11

鏈接練習參考答案

1.C. 2.A. 3.C. 4.CD.

(完)