平 征

(寧德師范學(xué)院數(shù)理學(xué)院,福建寧德 352100)

§1 引言

連通性是一類重要的拓?fù)湫再|(zhì),在拓?fù)鋵W(xué),分析學(xué),幾何學(xué)及相關(guān)的物理學(xué),計(jì)算機(jī)科學(xué)等學(xué)科中發(fā)揮了積極的作用.作為連通性的拓展,A.Fedeli和A.Le Donne[1]定義了拓?fù)淇臻g的序列連通性.H.C?akall?等[2-3]引入并研究了滿足第一可數(shù)公理的Hausdorff拓?fù)淙褐械腉連通性,并將序列連通性歸結(jié)為在通常收斂方法下的G連通性.林壽和劉麗[4]定義了一般集上的G方法及G收斂性,建立了較之于拓?fù)淇臻g中通常收斂性更為一般的收斂概念;隨后劉麗[5-7]研究了由G開集等確定的特殊集的性質(zhì)和G序列緊空間;而后吳永興和林福財(cái)[8]討論了拓?fù)淙旱腉連通相關(guān)性質(zhì)和G拓?fù)?接著平征[9]借助G方法,引入G隔離集,討論了一般集上的G連通性;近期劉麗和平征[10]引入了積集的G方法并討論了積集的G連通性.

在研究過程中發(fā)現(xiàn)了文[2]的定義1給出的G序列連通子集的定義有一些瑕疵,導(dǎo)致在此基礎(chǔ)上給出的四個等價條件并不成立.本文糾正了文[2]的定義1,給出了G序列連通子集的正確定義,并進(jìn)一步驗(yàn)證該定義與文[9]中的G連通子集的定義是一致的.文[4]中介紹了X的子集Y上的子方法G|Y,本文在此基礎(chǔ)上引入G|Y隔離集并定義了G|Y連通子集,討論了G|Y連通子集與G連通子集的關(guān)系.

§2 預(yù)備知識

設(shè)X是一個集,記s(X)是X中的所有序列組成的集,s(X)的元寫為x={xn}n∈N.設(shè)映射f:X →Y,記f(x)={f(xn)}n∈N.若X是一個拓?fù)淇臻g,記c(X)是X中的所有收斂序列所組成的集,集X上的一種方法(簡稱為G方法)是一個函數(shù)G:cG(X)→X,其中cG(X)?s(X).序列x∈s(X)稱為G收斂于l ∈X,若x∈cG(X)且G(x)=l.方法G:cG(X)→X稱為正則的[4],若c(X)?cG(X)且對任何x∈cG(X)有G(x)=lim x.方法G:cG(X)→X稱為子序列的[4],若x∈cG(X)且G(x)=l,且存在x 的子序列x′ ∈c(X)有l(wèi)im x′=l.

定義2.1[4]設(shè)X是一個集,G是集X上的一個方法且A ?X.

(1)A稱為X的G閉集,若x∈s(A)∩cG(X),則G(x)∈A.

(2)A稱為X的G開集,若X A是G閉集.

(3) 集∩{F:F是X的G閉集,且A ?F}稱為A的G閉包,記為.

對于集合X上的一個G方法及X上的任一子集A,A的G閉包是X的G閉集.

定義2.2[2]設(shè)X是一個集,G是集X上的一個方法且A ?X.A的子集F稱為A中的G閉集,若存在X的G閉集U使得F=U ∩A.V稱為A中的G開集,若AV是A中的G閉集.

引理2.3[11]設(shè)C是拓?fù)淇臻gX的連通子空間.如果X中有一對隔離子集X1和X2使得C ?X1∪X2,則有C ?X1或C ?X2.

定義2.4[9]設(shè)G是集X上的一個方法,若X的子集A,B滿足,則稱A,B是G隔離的.

定義2.5[9]設(shè)G是集X上的一個方法,Y ?X,若Y不能表示為X的一對非空G隔離集之并,則子集Y稱為G連通的.

定義2.6[4]設(shè)G是X上的一個方法,Y ?X.令cG|Y(Y)={x∈s(Y)∩cG(X):G(x)∈Y},G|Y:cG|Y(Y)→Y且G|Y(x)=G(x),x∈cG|Y(Y).則G|Y是X的子集Y上的子方法.

引理2.7[4]設(shè)G是X上的一個方法,A ?Y ?X,則

本文未定義的術(shù)語和符號,請參照文獻(xiàn)[11].

§3 G序列連通子集

文[2]定義1給出了G序列連通性的下述定義.

設(shè)G是集X上的一個方法,A ?X,A稱為G序列連通的,若不存在不交G閉子集U和V使得A ?U ∪V,且A ∩U和A ∩V是非空的.特別地,X稱為G序列連通的,若不存在非空,不交G閉子集U和V使得X=U ∪V.

在此基礎(chǔ)上,文[2]在引理1給出了G序列連通性的4個等價條件.

引理3.1[2]設(shè)G是集X上的一個方法,A ?X,下述條件等價：(i)A是G序列連通的;(ii)A不能表示成A中非空,不交G閉子集之并;(iii)A不能表示成A中非空,不交G開子集之并;(iv)不存在A中G開且G閉的真子集.

關(guān)于上述引理,給出下述例子.

例3.2設(shè)X=[0,2]賦予通常拓?fù)?G為通常收斂,G閉集即為閉集.取A=[0,1)∪(1,2]?X.下證A是G序列連通的.假設(shè)A不是G序列連通的,則存在不交閉集U,V使得A ?U ∪V,且?,?.因?yàn)閇0,1),(1,2]分別是連通的,由引理2.3不妨設(shè)[0,1)?U,(1,2]?V.因?yàn)閁,V為閉,所以1∈U ∩V.這與U,V不交相矛盾,因此A是G序列連通的.但是A=[0,1)∪(1,2],其中[0,1)=[0,1]∩A,(1,2]=[1,2]∩A分別是A中閉集,即A能表示為A中非空,不交閉集之并,所以A不滿足引理2.1的(ii).

正是由于上述G序列連通子集定義不恰當(dāng),導(dǎo)致引理3.1中的條件(i)與(ii)并不等價.

本文將文[2]關(guān)于G序列連通的定義修訂為下述定義3.3,并在此基礎(chǔ)上修改引理3.1為下述引理3.4.

定義3.3設(shè)G是集X上的一個方法,Y ?X,Y稱為G序列連通的,若Y不能表示成Y中非空,不交的G閉子集之并.

引理3.4設(shè)G是集X上的一個方法,Y ?X,下述條件等價.

(1)Y是G序列連通的;

(2)Y不能表示成Y中非空,不交G開子集之并;

(3) 不存在Y中非空G開且G閉的真子集.

證(1)?(2).假設(shè)Y能表示成Y中非空,不交G開集之并,即Y=U∪V,U和V均為Y中G開集,U ∩V=?.由于U和V均為Y中G開集,得Y U=V和Y V=U分別是Y中G閉集,即Y能表示成Y中非空,不交G閉子集之并,即Y不是G序列連通的.矛盾,從而(1)?(2).

(2)?(3).假設(shè)存在Y中非空G開且G閉的真子集U,則Y U也是Y中非空G開且G閉的真子集.Y=U ∪(Y U),且U ∩(Y U)=?,即Y能表示成Y中非空,不交G開子集之并.矛盾,從而(2)?(3).

(3)?(1).假設(shè)Y不是G序列連通的,則Y能表示成Y中非空,不交G閉子集之并,即Y=U ∪V,U和V均為Y中G閉集,U ∩V=?.由于U為Y中G閉集,可知V=Y U為Y中G開集,因此V為Y中非空G開且G閉的真子集.矛盾,從而(3)?(1).

通過下面討論可知上述所給出的G序列連通性實(shí)際上與定義2.5所給出的G連通性定義是一致的.

定理3.5設(shè)G是集X上的一個方法,Y ?X.Y是G序列連通與Y是G連通是一致的.

另一方面,假設(shè)Y不是G序列連通,則Y能夠表示為Y中一對非空,不交G閉子集A,B之并,即Y=A ∪B,A=U ∩Y,B=V ∩Y,A ∩B=U ∩V ∩Y=?,其中U,V分別是X中G閉.,同理.所以A,B為X上一對非空,不交G隔離集之并,因而Y不是G連通的.

綜上可得Y是G序列連通的與Y是G連通是一致的.

§4 G|Y 連通子集

定義4.1設(shè)G是X上的一個方法,Y ?X,若Y不能表示為Y上一對非空G|Y隔離集之并,則子集Y稱為G|Y連通的.

引理4.2設(shè)G是X上的一個方法,Y ? X,A,B ? Y.若A,B是X上一對G隔離集,則A,B是Y上一對G|Y隔離集.

定理4.3設(shè)G是集X上的一個方法且Y ?X.若Y是G|Y連通,則Y是G連通.

證假設(shè)Y不是G連通的,則存在X上一對非空G隔離集A,B使得Y=A ∪B,由引理4.2得,A,B是Y上一對G|Y隔離集,因此Y不是G|Y連通的,矛盾.

定理4.3的逆命題不一定成立.

例4.4存在集X上的一個方法G及Y ?X滿足

(1) 存在A,B是Y上G|Y隔離集,但不是X上G隔離集.

設(shè)X=[0,1],G是X上的一個方法,

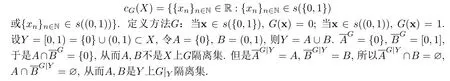
(2)Y是G連通,但不是G|Y連通.

由(1)可知Y不是G|Y連通的.下面證明Y是G連通的.

設(shè)Y=[0,1)=A∪B,A∩B=?,A,B非空.不妨設(shè)0,即0∈B,由A ?(0,1)知進(jìn)而故Y不能表示為X中一對非空G隔離集之并,從而Y是G連通的.

致謝本文是在林壽教授的悉心指導(dǎo)下完成的,特此致謝！