李 艷 ,趙燕冰 ,霍元極

(1.張家口學(xué)院 數(shù)學(xué)與信息科學(xué)學(xué)院,河北張家口 075000;2.張家口職業(yè)技術(shù)學(xué)院 基礎(chǔ)部,河北張家口 075000;3.河北北方學(xué)院理學(xué)院,河北張家口 075000)

§1 引言

在偏序集和格中的秩生成函數(shù)和特征多項(xiàng)式有許多文獻(xiàn)都做了介紹和研究[1-3],文獻(xiàn)[4]對(duì)一致偏序集作了進(jìn)一步的研究.有限域上的典型群幾何有著廣泛的應(yīng)用,如文獻(xiàn)[5]研究了偽辛空間中全迷向子空間的Critical問題,文獻(xiàn)[6-9]研究了在有限典型群作用下,由子空間軌道生成格的秩函數(shù)和特征多項(xiàng)式,并給出了相應(yīng)的定義和表示式.本文討論有限典型群的正交群O2ν+δ,Δ(Fn)作用奇特征正交空間下,子空間軌道生成格的秩生成函數(shù)和特征多項(xiàng)式.本文沿用文獻(xiàn)[1,9]中的名詞術(shù)語,并引用[1-2]和[9-10]中的一些結(jié)果.

設(shè)Fq是q個(gè)元素的有限域,q是一個(gè)素?cái)?shù)冪.是Fq上2ν+δ維行向量空間,其中ν是非負(fù)整數(shù),δ=0,1或2,charFq2,用[M1,M2,···,Ml]表示對(duì)角矩陣,其主對(duì)角線上依次是方陣.令上滿足TS2ν+δ,Δ tT=S2ν+δ,Δ的所有(2ν+δ)×(2ν+δ)的矩陣T,對(duì)矩陣的乘法作成一個(gè)群,稱為Fq上關(guān)于S2ν+δ,Δ的2ν+δ級(jí)正交群,記作O2ν+δ,Δ(Fq).它在上作用如下

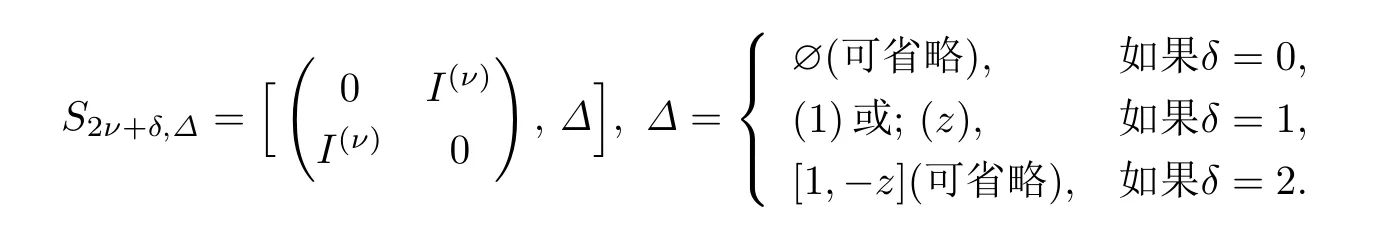
眾所周知PS2ν+δ,Δ tP合同于標(biāo)準(zhǔn)形[10]

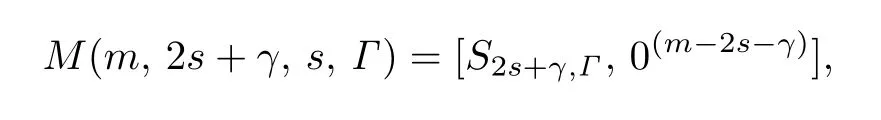
其中0≤s ≤[(m-γ)/2],Γ=0,1或2,并且

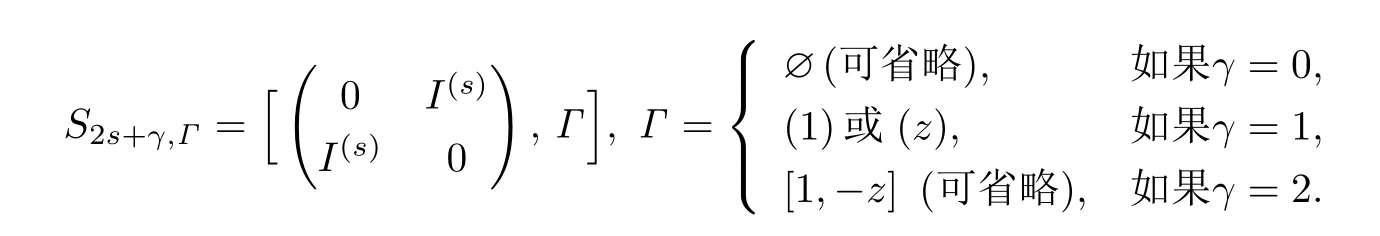
稱P是中關(guān)于S2ν+δ,Δ的(m,2s+γ,s,Γ)型子空間,簡稱(m,2s+γ,s,Γ)型子空間.

§2 預(yù)備知識(shí)

首先回顧文獻(xiàn)[9-10]中關(guān)于奇特征有限幾何理論的一些基本知識(shí).

引理2.1(見[9,p60]) 在中,關(guān)于S2ν+δ,Δ存在(m,2s+γ,s,Γ)型子空間當(dāng)且僅當(dāng)

用M=M(m,2s+γ,s,Γ;2ν+δ,Δ)表示中關(guān)于S2ν+δ,Δ的全體(m,2s+γ,s,Γ)型子空間的集合.當(dāng)δ=0或2時(shí),分別寫成M(m,2s+γ,s,Γ;2ν)或M(m,2s+γ,s,Γ;2ν+2).M是中的子空間集在正交群O2ν+δ,Δ(Fq)作用下的一條軌道[9-10].

令L(M)=L(m,2s+γ,s,Γ;2ν+δ,Δ)是M中子空間非空交組成的集,約定是M中0個(gè)子空間的交.如果按子空間的反包含關(guān)系,規(guī)定L(m,2s+γ,s,Γ;2ν+δ,Δ)的偏序≥,即對(duì)于的子空間U,W,有.那么L(m,2s+γ,s,Γ;2ν+δ,Δ)作成有限格,稱為由M(m,2s+γ,s,Γ;2ν+δ,Δ)生成的格,記為LR(m,2s+γ,s,Γ;2ν+δ,Δ).由[9]中定理5.12,如果

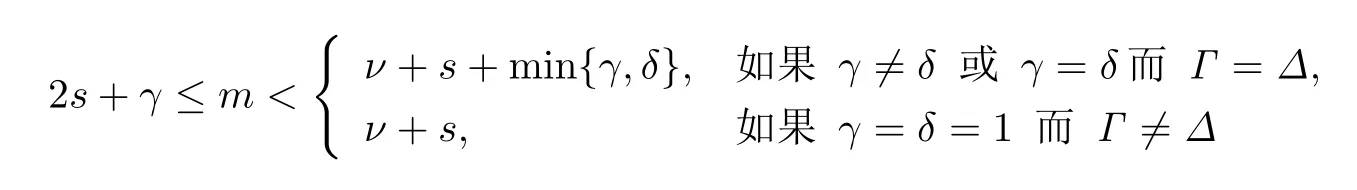
成立,那么LR(m,2s+γ,s,Γ;2ν+δ,Δ)由和滿足

的所有(m1,2s1+γ1,s1,Γ1)型子空間組成.如果

成立,那么LR(m,2s+γ,s,Γ;2ν+δ,Δ)由和滿足(2)而不列入文獻(xiàn)[9]中表5.5中的所有(m1,2s1+γ1,s1,Γ1)型子空間組成.

定義2.1[9]設(shè)P是有0的偏序集,N0是非負(fù)整數(shù)所成的集合.函數(shù)

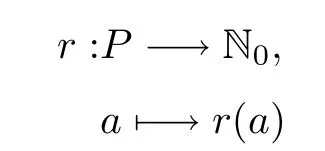
叫P上的秩函數(shù),如果下面的(i)和(ii)成立.

(i)r(0)=0;

(ii) 對(duì)于a,b ∈P而ab[9],那么r(b)=r(a)+1.

若含有0的有限偏序集P中,P的所有極大鏈都具有相同的長度n,則稱P的秩為n,記為r(P)=n,并且稱P為秩n的分次偏序集,如果此偏序集是格,就稱它為秩n的分次格.

定義2.2[2]若P是秩n的分次偏序集,并且其中有pi個(gè)元素的秩為i,則稱多項(xiàng)式

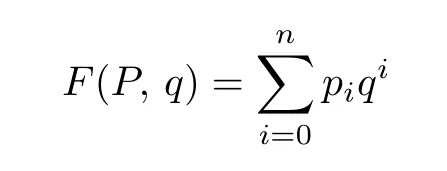
為P的秩生成函數(shù).當(dāng)P是一個(gè)格L時(shí),F(P,q)就稱為格L的秩生成函數(shù).

引理2.2(見[9,p97]) 設(shè)n=2ν+δ ＞m ≥1,而(m,2s+γ,s,Γ)滿足引理2.1中(1)式,對(duì)于

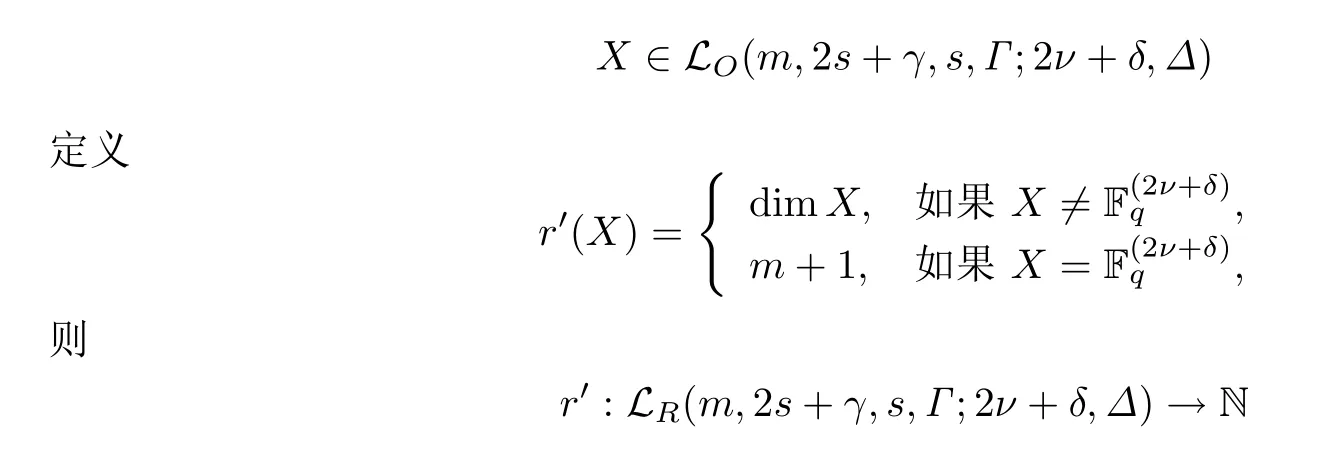
是格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩函數(shù).

定義2.3[9]設(shè)P是有最小元0和最大元1的有限偏序集,并且P上有秩函數(shù)r和M?bius函數(shù)μ,那么多項(xiàng)式

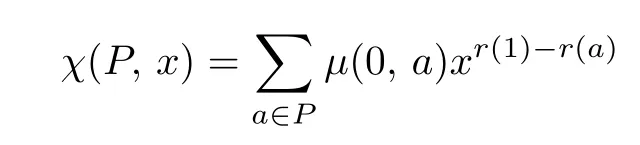
叫做P上的特征多項(xiàng)式.

§3 主要結(jié)果

關(guān)于格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩生成函數(shù),特征多項(xiàng)式有如下結(jié)果.為了表述上的方便,記

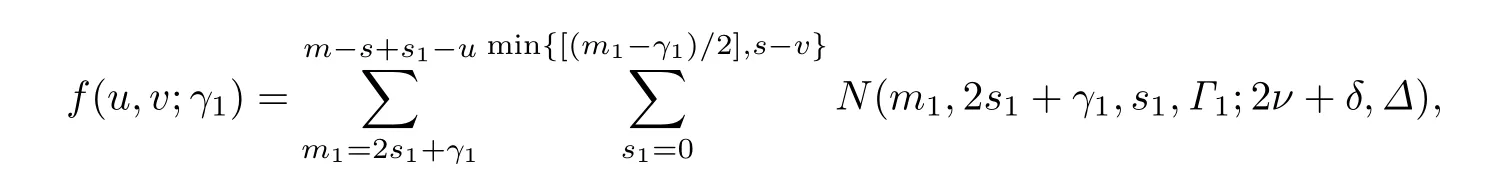
其中(m1,2s1+γ1,s1,Γ1)滿足引理2.1中(1)和(2)而γ1=0,1或2,

定理3.1設(shè)1≤m1≤m ≤2ν+δ-1,子空間(m,2s+γ,s,Γ)與(m1,2s1+γ1,s1,Γ1)滿足(1)式且(2)式成立

(i) 如果γ=0,那么LR(m,2s,s;2ν+δ,Δ)的秩生成函數(shù)是

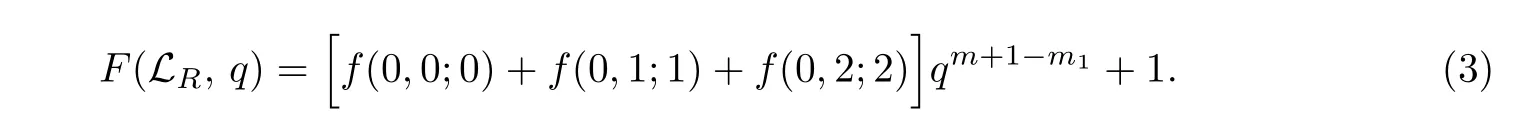
(ii) 如果γ=1,那么LR(m,2s+1,s,Γ;2ν+δ,Δ)的秩生成函數(shù)是

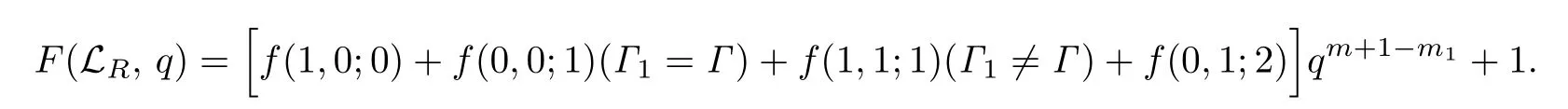
(iii) 如果γ=2,那么LR(m,2s+2,s,Γ;2ν+δ,Δ)的秩生成函數(shù)是

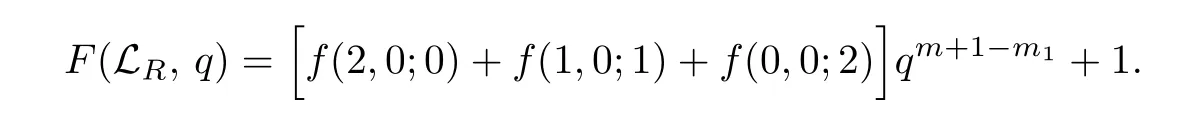
證由引理2.2知,對(duì)于X ∈LR(m,2s+γ,s,Γ;2ν+δ,Δ),定義

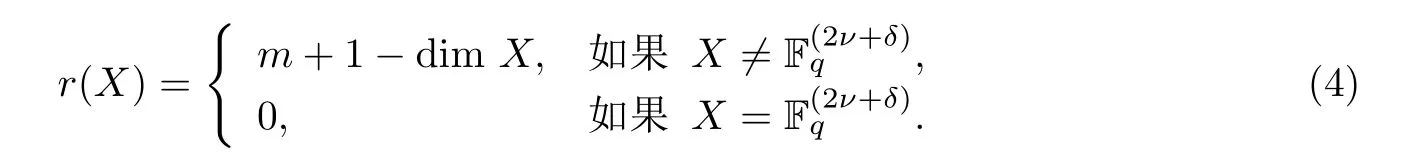
那么r:LR(m,2s+γ,s,Γ;2ν+δ,Δ)→N0是格LR(m,2s+γ,s,Γ;2ν+δ,Δ)的秩函數(shù).

設(shè)P ∈LR(m,2s+γ,s,Γ;2ν+δ,Δ),考慮到LR(m,2s+γ,s,Γ;2ν+δ,Δ)中子空間的組成,如果,那么r(P)=0,所以LR(m,2s+γ,s,Γ;2ν+δ,Δ)中秩為0的子空間個(gè)數(shù)是1.由文獻(xiàn)[9]中定理5.10可知

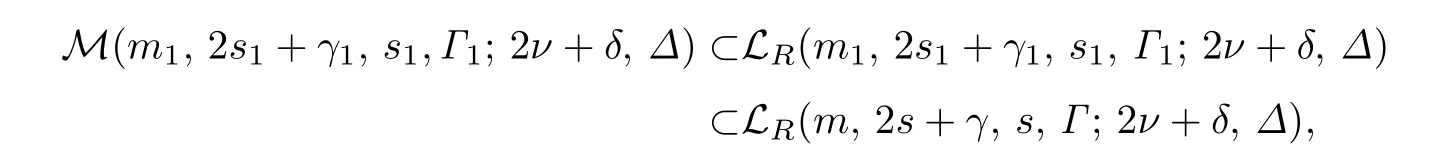
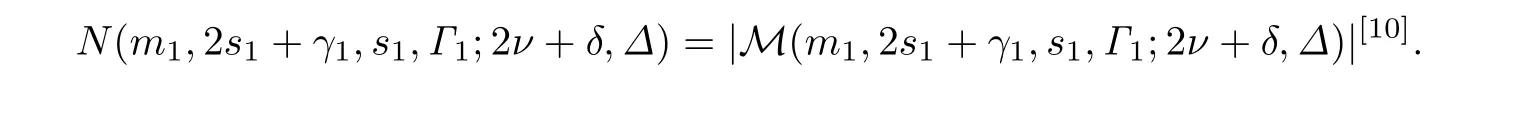
只證明情形(i),對(duì)于情形(ii),(iii)類似可證.下面分別對(duì)γ1=0,1或2進(jìn)行計(jì)算.

a)γ1=0.這時(shí)(1) 式成為

(2)式變成

在m1取定后,s1滿足0≤s1≤min{[m1/2],s}.所以當(dāng)(m1,2s1+γ1,s1,Γ1)滿足(1) 和(2)時(shí),秩為i=m+1-m1的子空間P的個(gè)數(shù)是

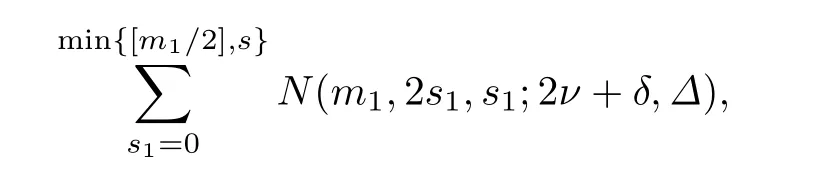
由(6)有0≤m1≤m-s+s1,所以m-s+s1≤ν+s1.由(5)和m1≤m-s+s1,可得2s1≤m1≤m-s+s1.因此當(dāng)(m1,2s1,s1)滿足(1)和(2)時(shí),LR(m,2s+γ,s,Γ;2ν+δ,Δ)中F(2ν+δ)q的個(gè)數(shù)是

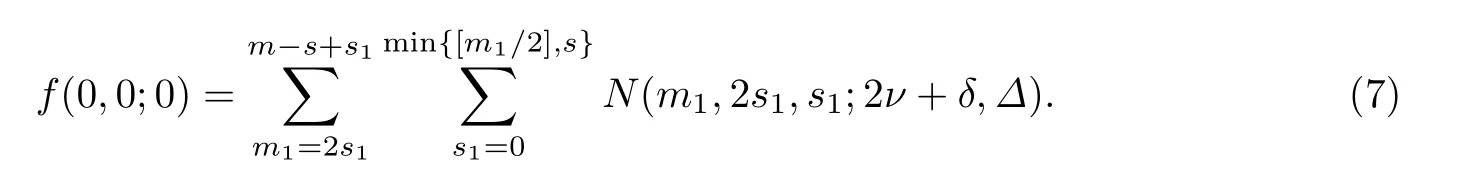
b)γ1=1.這時(shí)(1)式成為

(2)式變成

在m1取定后,s1滿足0≤s1≤min{[(m1-1)/2],s -1},所以在(m1,2s1+1,s1,Γ1)滿足(1)和(2)時(shí),秩為i=m+1-m1的子空間P的個(gè)數(shù)是

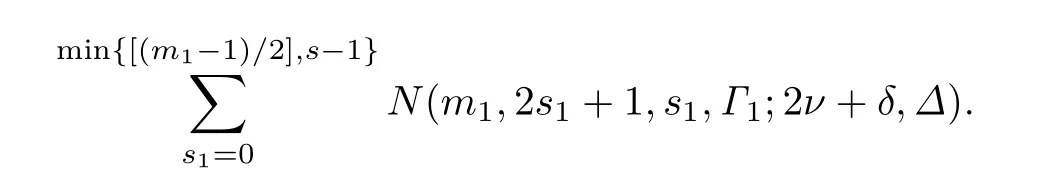
由(9)有0≤m1≤m-s+s1,從(8)和m1≤m-s+s1,可得2s1+1≤m1≤m-s+s1.所以在(m1,2s1+1,s1,Γ1)滿足(1)和(2)時(shí),LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的個(gè)數(shù)是

c)γ1=2.這時(shí)(1)式成為

(2)式變成

在m1取定后,s1滿足0≤s1≤min{[(m1-2)/2],s-2},所以在(m1,2s1+2,s1)滿足(1)和(2)時(shí),秩為i=m+1-m1的子空間P的個(gè)數(shù)是

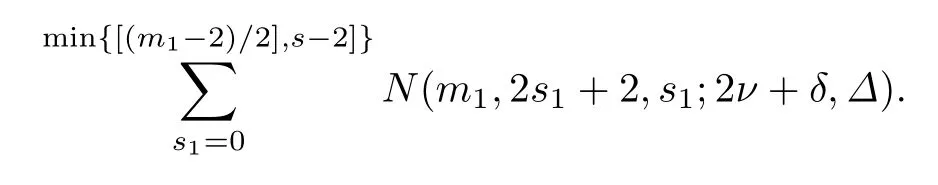
由(12)有0≤m1≤m-s+s1.從(11)和m1≤m-s+s1可得2s1+2≤m1≤m-s+s1.所以在(m1,2s1+2,s1)滿足(1)和(2)時(shí),LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的個(gè)數(shù)是

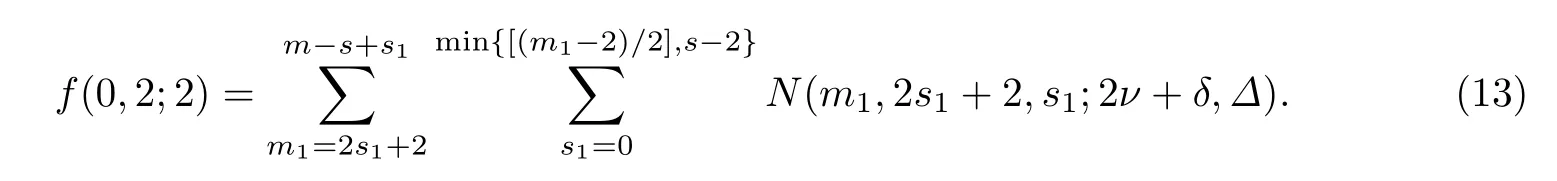
定理3.2設(shè)n=2ν+δ ＞m ≥1,并且(m,2s+γ,s,Γ)滿足(1)式.

(i) 如果γ=0,那么特征多項(xiàng)式χ(LR(m,2s,s;2ν+δ,Δ),x)為

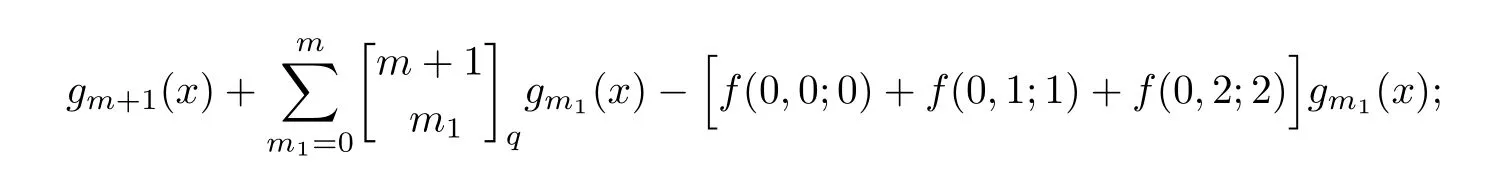
(ii) 如果γ=1,那么特征多項(xiàng)式χ(LR(m,2s,s;2ν+δ,Δ),x)為

(iii) 如果γ=2,那么特征多項(xiàng)式χ(LR(m,2s,s;2ν+δ,Δ),x)為

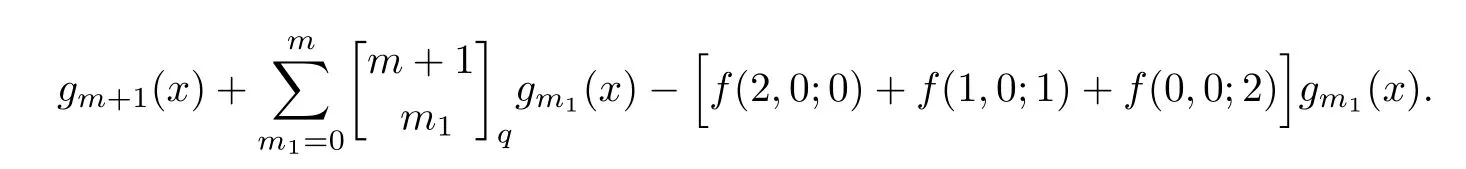
其中g(shù)m+1(x),gm1(x)為Gauss多項(xiàng)式[9],x為未知元.

證由(4)式及引理2.2,可知r是LR(m,2s+γ,s;2ν+δ,Δ)的秩函數(shù).

和r(X)=m+1-dimX,,并且特征多項(xiàng)式χ(L1,x)=χ(LR(Fm+1),x),而L0的最大元和最小元分別是0和V0,L1的最大元和最小元分別是0和V1所以L0和L1的特征多項(xiàng)式分別是

對(duì)上述兩個(gè)等式進(jìn)行M?bius 反演,可得

取定滿足(1)和(2)的(m1,2s1+γ1,s1,Γ1),那么由[10]中的定理6.26,可知

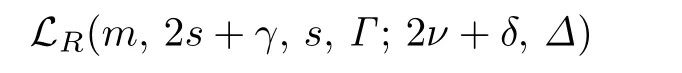
中(m1,2s1+γ1,s1,Γ1)型子空間的個(gè)數(shù)是N(m1,2s1+γ1,s1,Γ1;2ν+δ,Δ).因?yàn)長1{V1}中m1維子空間的個(gè)數(shù)是所以

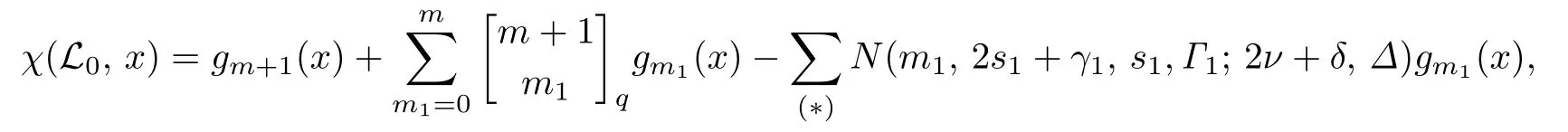
其中(*)表示(m1,2s1+γ1,s1,Γ1)滿足(1)和(2).

在定理3.1的證明中,對(duì)γ=0,1,或2分別算出了滿足(1)和(2)的LR(m,2s+γ,s,Γ;2ν+δ,Δ)中的個(gè)數(shù)及其表示式,將其代入上式可得定理3.2.

作為定理3.2的特殊情形,有如下結(jié)果.

推論3.3設(shè)n=2ν+δ ＞1,那么

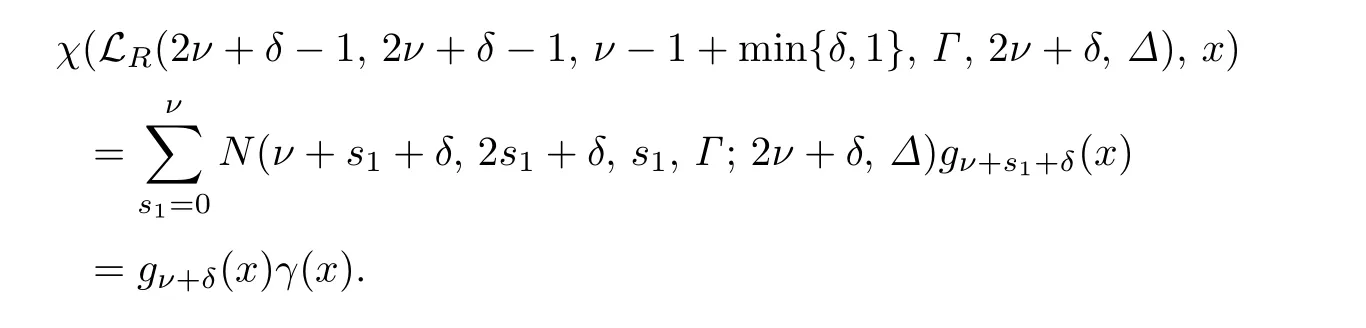
其中g(shù)ν+s1+δ(x),gν+δ(x)為Gauss多項(xiàng)式,γ(x)∈Z[x]是首一多項(xiàng)式.

證類似于文獻(xiàn)[9]中推論8.20的證明,可證推論3.3.