尹天樂 龐 晶

(1.內蒙古工業(yè)大學,理學院,內蒙古呼和浩特 010051;2.內蒙古自治區(qū)生命數(shù)據(jù)統(tǒng)計分析理論與神經(jīng)網(wǎng)絡建模重點實驗室,內蒙古呼和浩特 010051)

§1 引言

近年來,隨著對孤子理論的研究,學者們逐步建立和構造起來一些以計算機符號為主的求解代數(shù)方法,而直接代數(shù)法具有應用范圍較為廣泛,容易實現(xiàn)以及效率較為高的優(yōu)勢.并且,直接代數(shù)法又包含了展開法[1-2],雙曲函數(shù)展開法[3-6],exp(-φ(ξ))展開法[6-7],Jacobi橢圓函數(shù)展開法[8-10],輔助方程法[11-14]等,這些方法都具有相似的求解過程,其求解步驟主要分為四步.(在參考文獻中均有體現(xiàn))

1.對給定非線性發(fā)展方程進行行波變換,得到常微分方程;

2.引入輔助方程,并根據(jù)齊次平衡原則設解;

3.將輔助方程代入到常微分方程中,并且令相關整式的各次冪系數(shù)為0,得到一個代數(shù)方程組;

4.求解代數(shù)方程組,并利用輔助方程的解得到給定非線性發(fā)展方程的精確行波解.

為方便表達,將類似于上述求解過程的方法統(tǒng)稱為輔助方程法.

各種輔助方程法的主要不同之處是所選擇的輔助方程,在展開法中,所選取的輔助方程是二階線性常微分方程(15);在雙曲正切函數(shù)展開法中,所選取的輔助方程是(20);在Jacobi橢圓函數(shù)展開法中,輔助方程類似于(2),等等.簡言之,大多數(shù)輔助方程可以分為三類: 二階常微分方程和廣義Riccati方程

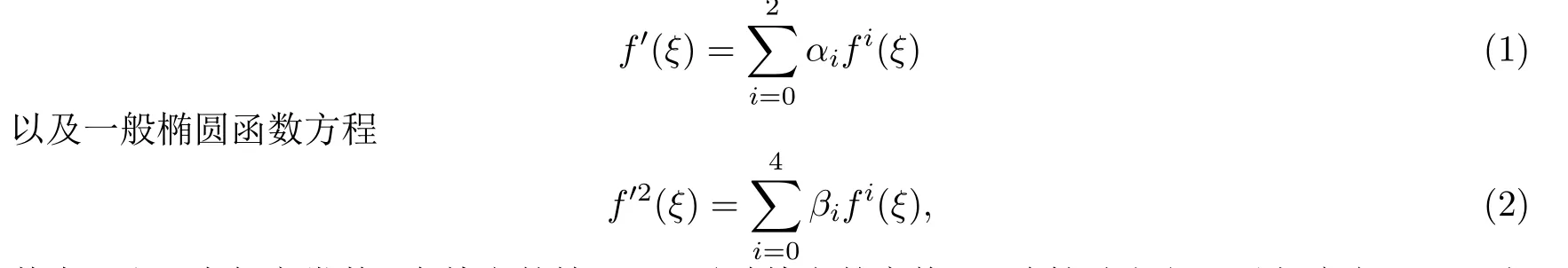
其中αi和βi為任意常數(shù).在特定的情況下,通過特定的變換,二階輔助方程可以與廣義Riccati方程或一般橢圓函數(shù)方程相互轉換,例如,對式(1)做變換可以得到式(15),反之同理.

由于各種輔助方程法所引入的輔助方程不盡相同,那么所設的解也不盡相同,例如在exp(-φ(ξ))展開法中,設解為

其中,ηi(i=1,2,3,···,n)為待定未知量;在雙曲正切函數(shù)法[6]中,設解為

等等.所以在求解非線性發(fā)展方程時,可否僅依據(jù)方程的自身得到解? 在廣田雙線性方法[14-17]中,可以通過有理變換(11)得到一個對數(shù)函數(shù)形式的解,但是在求解變系數(shù)非線性發(fā)展方程時會比較困難.

本文總結前人的方法與經(jīng)驗,在處理變系數(shù)非線性發(fā)展方程時,將傳統(tǒng)輔助方程法改進,在做行波變換之前引入有理變換,并通過特定的方式得到給定方程的初步的解,再依據(jù)輔助方程等得到變系數(shù)非線性發(fā)展方程的精確行波解.§2較為詳細地說明了本文的方法過程;§3-§5分別用展開法,展開法和橢圓函數(shù)展開法的輔助方程求解了一類KdV方程.結果表明,本文所給的方法是適用于多種輔助方程,并且通過有理變換等手段可以求得變系數(shù)非線性發(fā)展方程的一個相對統(tǒng)一的解.與傳統(tǒng)輔助方程法相比較,其優(yōu)勢在于無需依據(jù)各種輔助方程法的特性去設解,并且在求解過程中可以省去如設解(3),(4)中出現(xiàn)的ηi等多個待定未知量,這使計算過程更加方便簡潔.更重要的是,本文的方法可以將多種輔助方程法的求解過程統(tǒng)一化,進一步完善輔助方程法的研究理論.

§2 方法簡介

本節(jié)簡單說明所給的方法.現(xiàn)引入變系數(shù)非線性偏微分方程

其中u=u(x,t)是未知函數(shù).

步驟一 首先作有理變換(11)代入到(5)中,得到由F(x,t)和G(x,t)及它們的各階微分組成的等式

其中F=F(x,t),G=G(x,t)是未知函數(shù).(一般地,為了簡便計算,在作有理變換之前,根據(jù)不同方程的不同特點,需要引入u=wx或者u=wxx將方程轉化為等價形式)*

步驟二 從(6)中選取兩個特定的項Φ和Ψ,令Φ+Ψ=0,可以得到F(x,t)和G(x,t)的關系,然后根據(jù)有理變換可以得到方程(5)的解

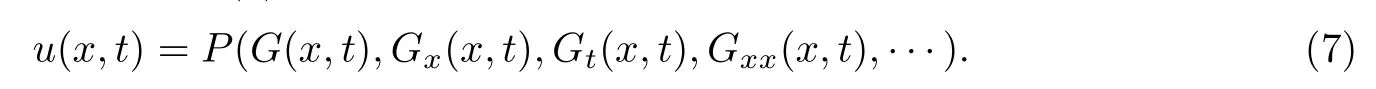
在這里,Φ和Ψ需要滿足如下條件.

1.Φ是由式(5)中最高階線性項進行有理變換所得到的項,Ψ是由式(5)中最高冪次的非線性項進行有理變換所得到的項.

2.Φ和Ψ均是由F(x,t)和G(x,t)及它們的一階微分組成的項.

步驟三 做行波變換G(x,t)=G(ξ),其中ξ=kx+ω(t),并且引入輔助方程,例如(15),(25),(32)等.

步驟四 將F(x,t)和G(x,t)的關系,行波變換以及輔助方程帶入到(6)后,令關于G(ξ)的整式各次冪的系數(shù)為0,則得到以k和ω(t)為未知量的一個線性代數(shù)方程組.

步驟五 借助計算機軟件Mathematica求解步驟四中得到的代數(shù)方程組,以確定相關的待定未知量.然后將F(x,t)和G(x,t)的關系,行波變換以及輔助方程帶入到解(7)中,再依據(jù)輔助方程的解和代數(shù)方程組的解,便可得到方程(5)的精確行波解.

*: 在作有理變換之前引入u=wx或者u=wxx有利于方便計算,§3 KdV方程為例,其原因主要有以下兩點理由.

一.由于方程(8)中最高階的線性項為u3x的階數(shù)是O(u3x)=n+3,最高冪次的非線性項為uux的階數(shù)是O(uux)=2n+1,平衡得到n=2;然而,在方程(10)中平衡得到n=1,所以方程(10)的截斷形式級數(shù)解要優(yōu)于方程(8)的.

本文的其它方程同理,讀者可自行驗證.

§3 改進輔助方程法―展開法在變系數(shù)KdV方程中的應用

展開法是王明亮等人于2008年提出的一種構造非線性發(fā)展方程精確行波解的方法,其選取的輔助方程為二階線性微分方程(15).本節(jié)應用展開法的輔助方程求解變系數(shù)KdV方程

代入到方程(8)后對x進行積分并且取積分常數(shù)為0,將其化成等價形式

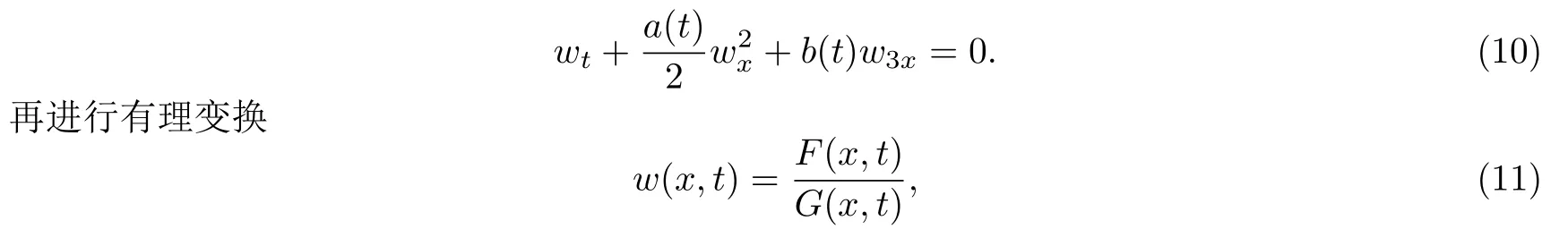
代入到式(10),整理得到

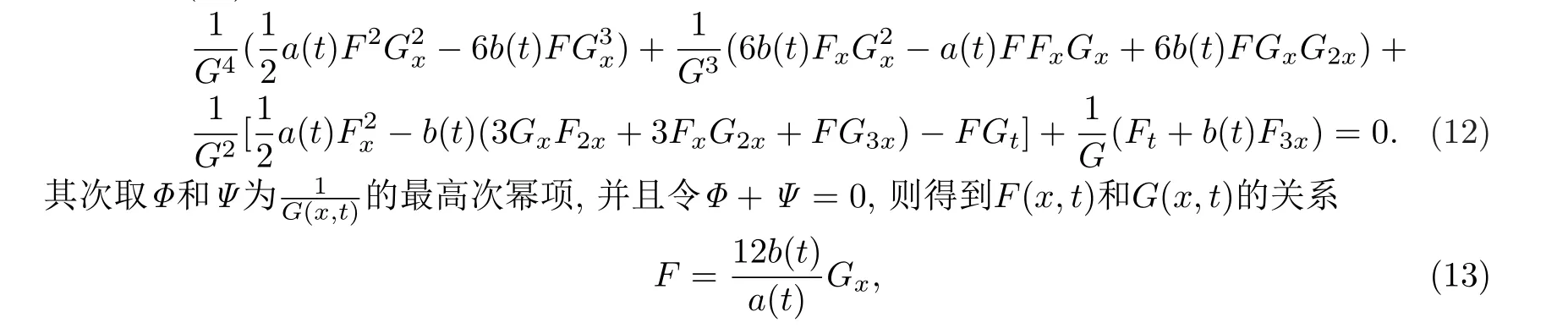
再根據(jù)之前進行的有理變換得到方程(8)的解

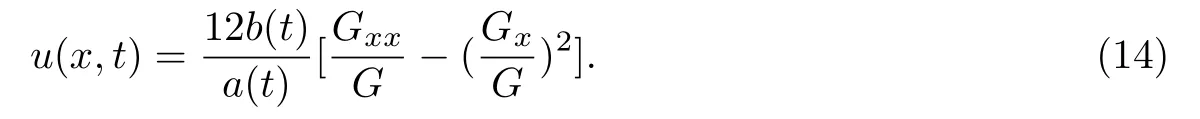
然后做行波變換G(x,t)=G(ξ),其中ξ=kx+ω(t),G(ξ)為輔助方程

其中a3為任意非0常數(shù).

最后將行波變換以及輔助方程(15)帶入到解(14)中,得到

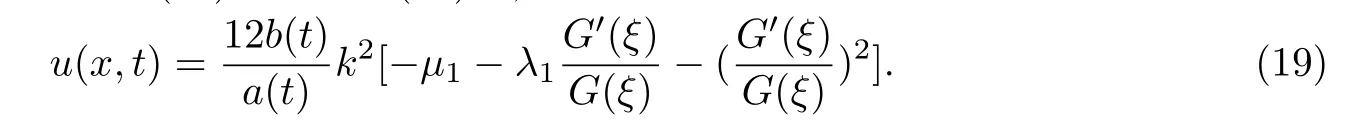
再根據(jù)輔助方程的解(16)和代數(shù)方程組的解(18),可以得到如下所示的變系數(shù)KdV方程(8)的精確行波解.

當Δ ＞0時有

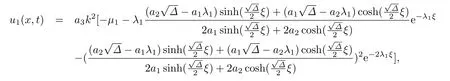
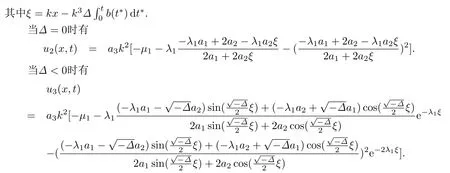
注對于本節(jié)情況,若輔助方程(15)的λ1=0,變換可以得到

實際上,(20)是雙曲正切函數(shù)展開法的輔助方程,只需要令即可.也就說,雙曲正切函數(shù)展開法可以由本文所給方法進行改進,并且輔助方程(20)同樣適用于本方法.

§4 改進輔助方程法―展開法在變系數(shù)mKdV 方程中的應用

變系數(shù)mKdV方程

可用于非調和晶格中描述等離子和聲子多重作用的孤立子模型.對于該方程而言,可以直接進行有理變換,則得到類似于上一節(jié)情況,故本節(jié)不再說明,而本節(jié)選取的輔助方程是展開法中的(25).

同樣引入(9),代入到方程(21)后對x進行積分并且取積分常數(shù)為0,將其化成等價形式

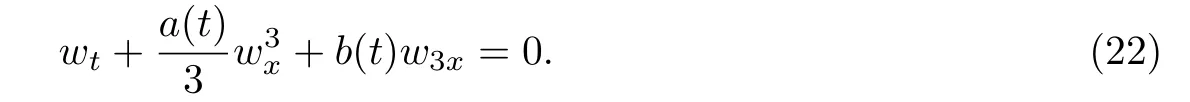
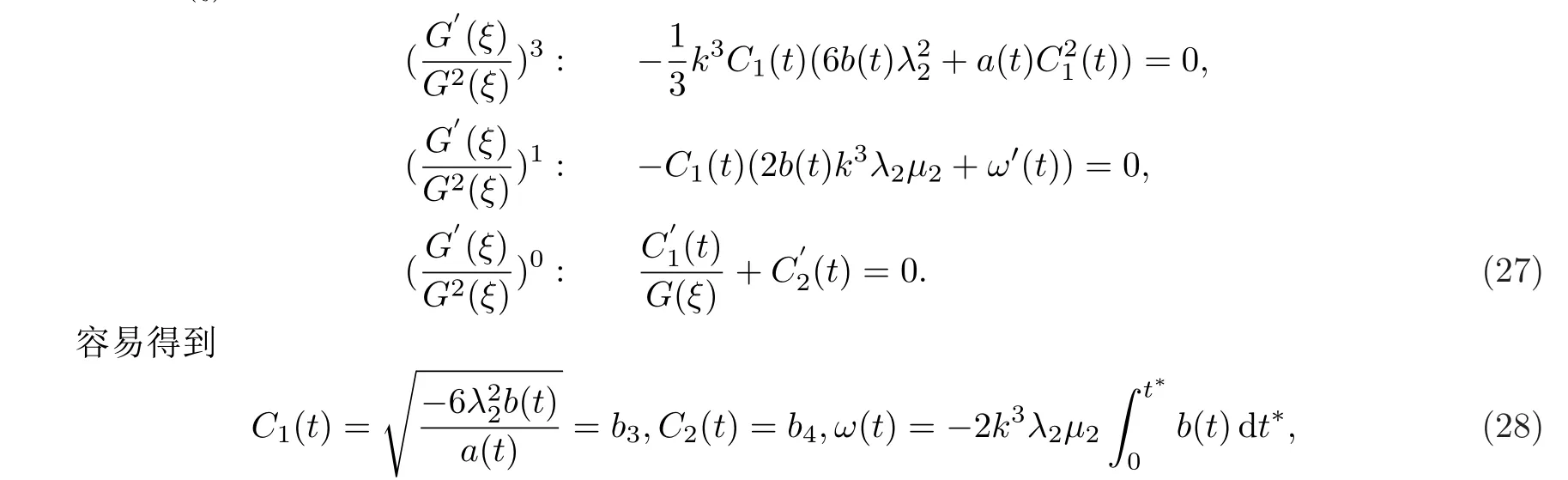
其中b3和b4為任意非0常數(shù).

最后將行波變換以及輔助方程(25)帶入到解(24)中,再根據(jù)輔助方程的解(26)和代數(shù)方程組的解(28),可以得到如下所示的變系數(shù)mKdV方程的精確行波解.

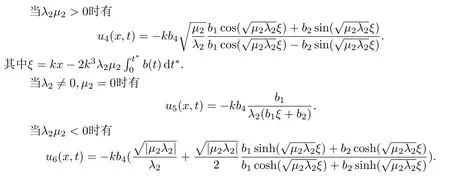
§5 改進輔助方程法―橢圓函數(shù)法在變系數(shù)fKdV方程中的應用

本節(jié)以變系數(shù)fKdV方程

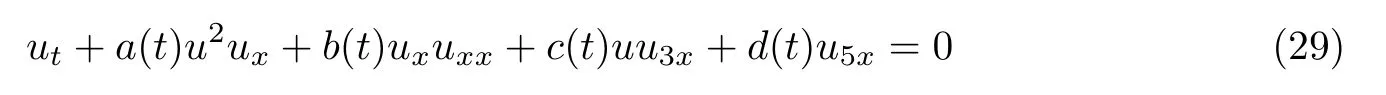
為例,所引入的輔助方程為第四類橢圓方程(32).

首先引入(9)代入到式(29)后對x進行積分并且取積分常數(shù)為0,將其化成等價形式

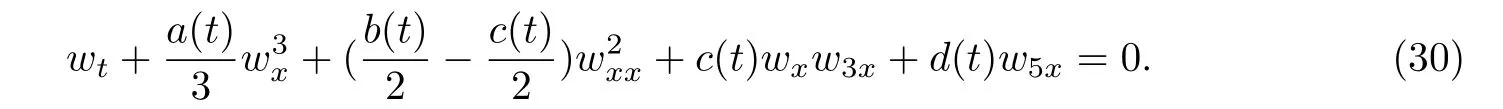
其次取Φ和Ψ為的最高冪次項,可以得到類似于(13)的關系,再根據(jù)有理變換得到解

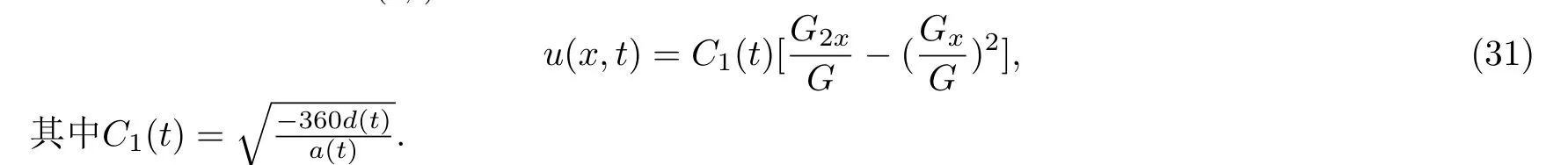
然后做行波變換G(x,t)=G(ξ),同樣有ξ=kx+ω(t),G(ξ)為輔助方程

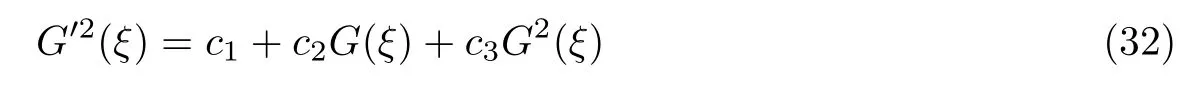
的解,其中c1,c2,c3為常數(shù).文獻[8]給出了方程(32)的多個精確解,并且在[13]中作者將該方程的解進行了等價性證明和分類,故方程(32)的解如下.

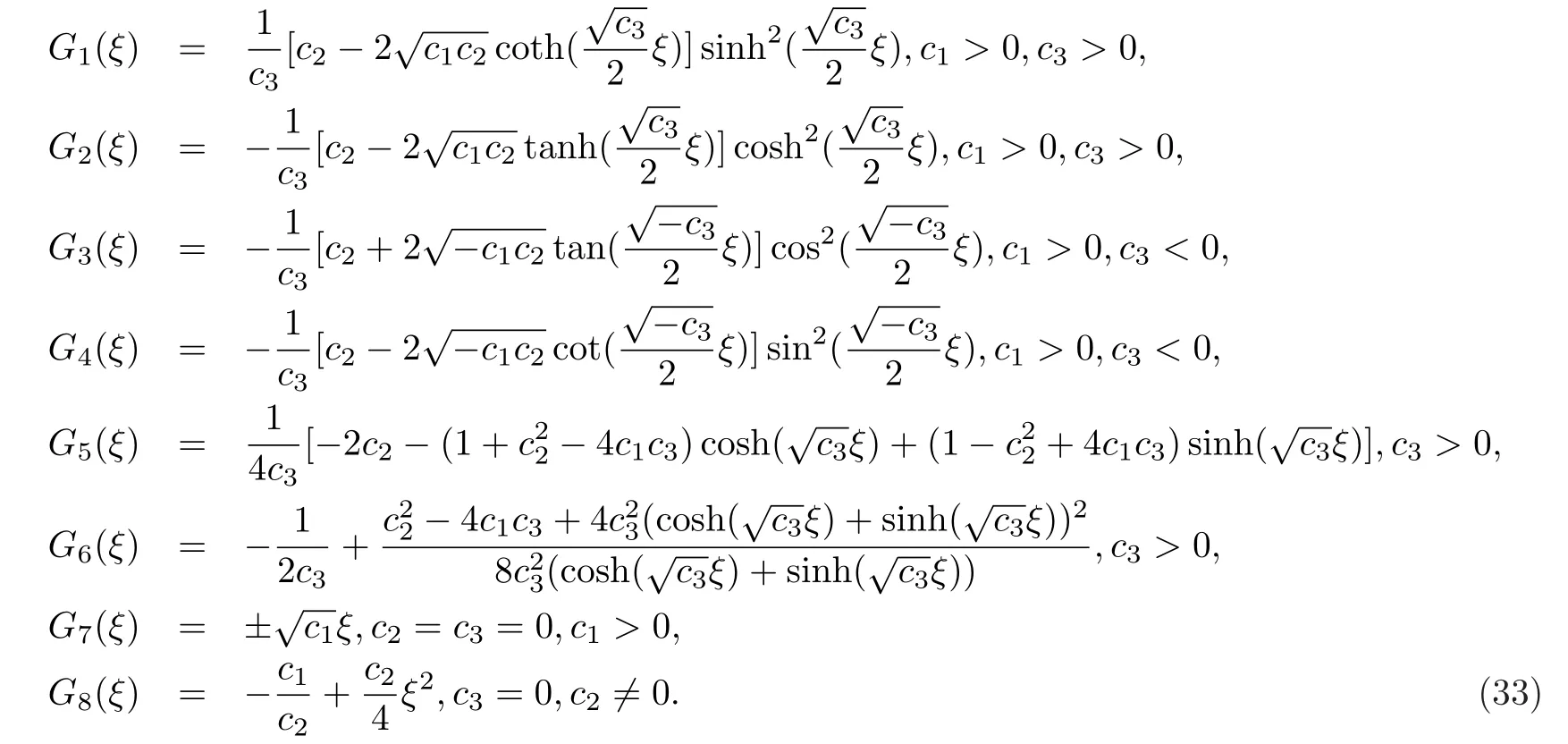
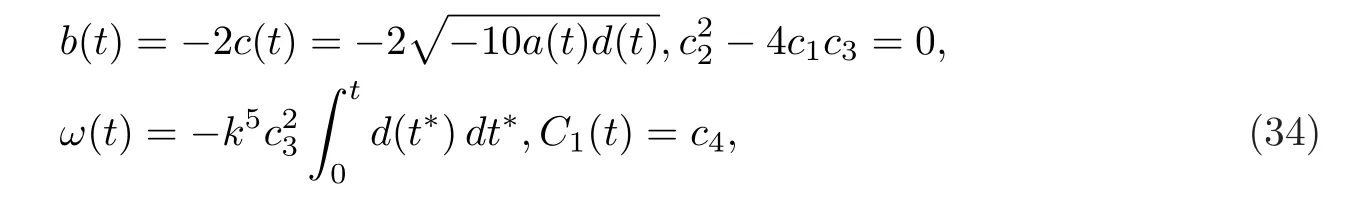
其中c4為任意常數(shù).

最后由行波變換,式(31),式(34)和輔助方程(32)及其解,可以得到如下所示的非線性方程(29)的精確行波解.

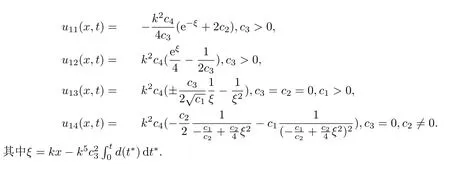
§6 解及圖像的簡要分析

本文運用改進輔助方程法得到了有理函數(shù),三角函數(shù)和雙曲函數(shù)解.由于變系數(shù)KdV方程和mKdV方程的解較為常見,并且在文獻中有所體現(xiàn),故本文僅對變系數(shù)fKdV方程的部分解進行圖像展示和說明.圖1-圖6分別是解u7-u12的圖像,其左側圖為三維圖像,而圖1-圖4的右側圖是取t=0時的二維圖像,圖5和圖6的右側圖是取x=0時的二維圖像.通過對ci(i=1,2,3,4)取值,和d(t)取不同的函數(shù)時,得到了一些孤子解.圖1,圖4是孤子解,圖2,圖3是扭曲孤子解,圖5,圖6是周期亮孤子解.

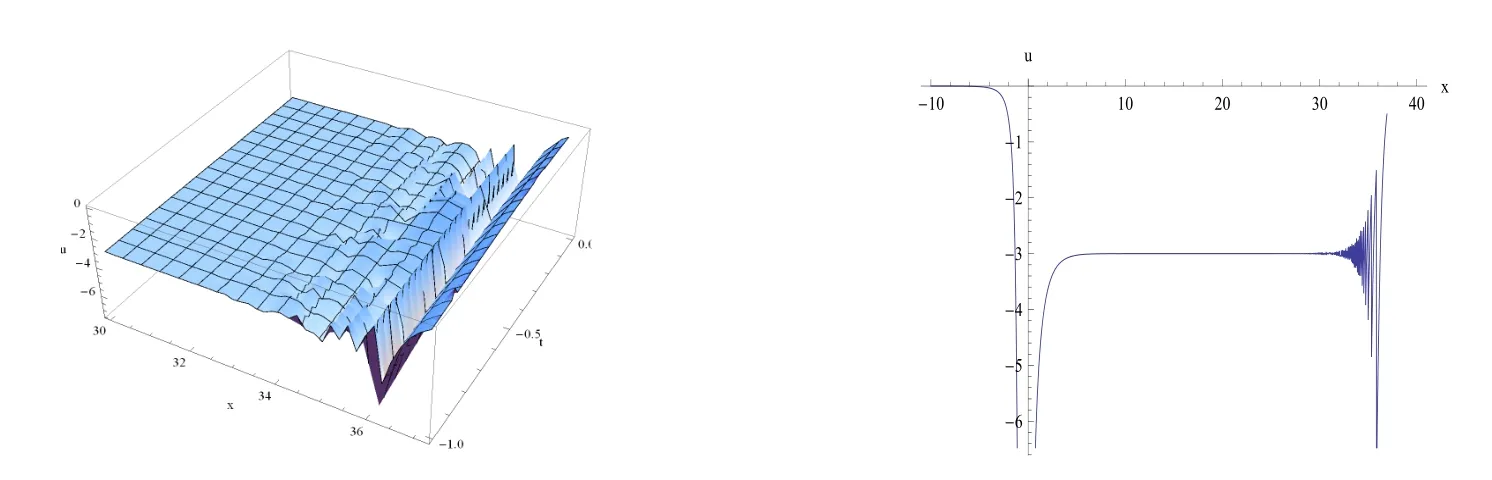
圖1 解u7的演變: c1=1,c2=4,c3=4,c4=1,d(t)=t,k=1

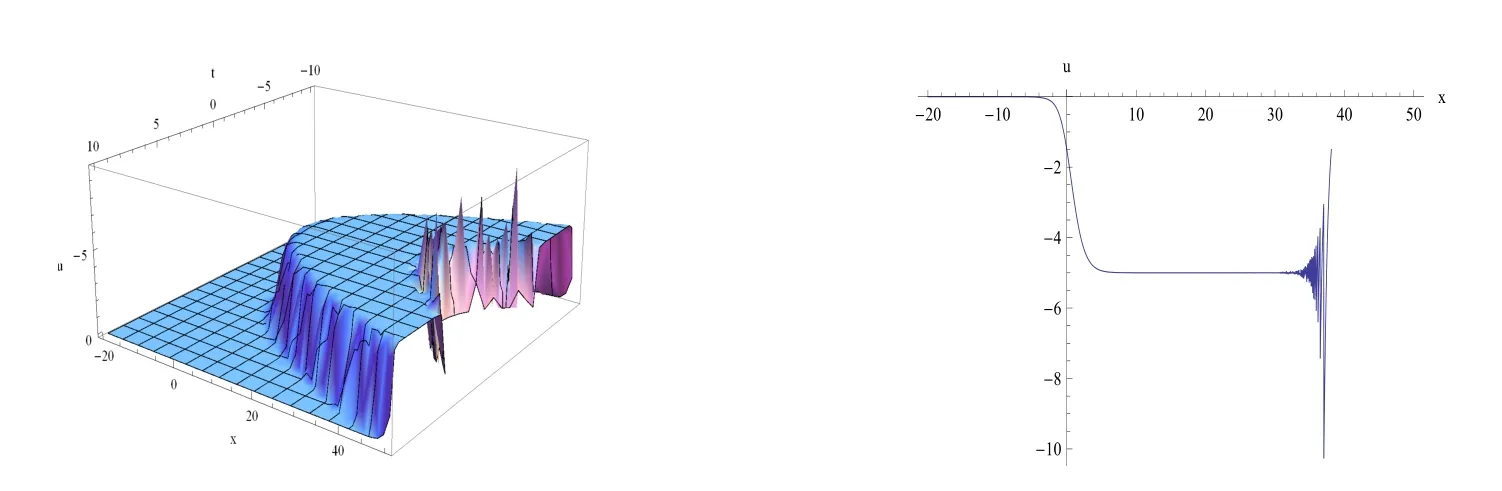
圖2 解u8的演變: c1=1,c2=2,c3=1,c4=1,d(t)=t,k=1

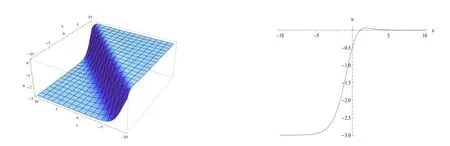
圖3 解u9的演變: c1=1,c2=4,c3=4,c4=1,d(t)=t,k=1

圖4 解u10的演變: c1=1,c2=4,c3=4,c4=1,d(t)=sin(t),k=1

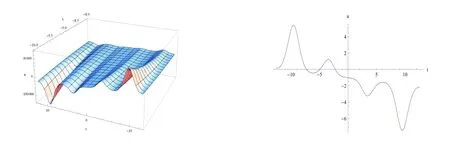
圖5 解u11的演變: c1=1,c2=2,c3=1,c4=1,d(t)=+sin(t),k=1

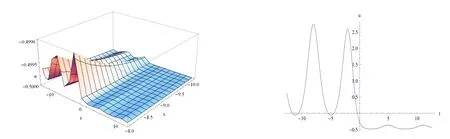
圖6 解u12的演變: c1=1,c2=2,c3=1,c4=1,d(t)=sin(t),k=1

§7 總結

本文成功地將有理變換融入到輔助方程法中,使幾類輔助方程法擁有統(tǒng)一的求解過程.與其他的方法相比較,本文所給出的方法將多個待定未知量省去,極大的簡化了計算量,并且使用符號計算機系統(tǒng)Mathematica,成功地使計算過程變得清晰簡潔,具有簡單易懂,計算量較少,易于求解的特點,并且在求解變系數(shù)發(fā)展方程時更具有優(yōu)勢.故本文為變系數(shù)非線性發(fā)展方程的研究提供了一個新的思想,并且為更高階更高維的變系數(shù)方程進一步開拓了研究與探索的新思路.