呂梓帆,張順利

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

非線性系統(tǒng)的研究在自然科學(xué)領(lǐng)域有著非常重要的作用,描述非線性系統(tǒng)的方法有很多種,如遞推算子法,Darboux變換法,M¨obious變換法等[1-2],其中對(duì)稱群理論和Painlev′e分析法在構(gòu)造精確解的過程中起著重要的作用.近年來,樓森岳教授等人發(fā)現(xiàn)了Painlev′e分析也可用于獲取非局域?qū)ΨQ,對(duì)應(yīng)于Painlev′e截?cái)嗾归_的奇異流形的留數(shù),因此也被稱為留數(shù)對(duì)稱.此外,文獻(xiàn)[3-5]還進(jìn)一步推廣了Painlev′e截?cái)嗾归_方法,引入了“一致Riccati展開可解性”的定義,這對(duì)于構(gòu)建相互作用解和新的可積系統(tǒng)有重要意義.目前,很多方程的精確解都可以利用上述方法構(gòu)造出來,如Korteweg-de Vries方程,Burgers方程,色散長波方程,非線性Boussinesq方程,Boussinesq-Burgers方程,Kadomtsev-Petviashvili方程,Benjamin-Bona-Mahony方程等[6-14].

文獻(xiàn)[15]提出的著名的淺水波運(yùn)動(dòng)方程在其他物理研究中[15],也可以作為一種長波模型,用于解釋孤立波的相互作用和無耗散的波狀激發(fā)等現(xiàn)象.當(dāng)物理參數(shù)被適當(dāng)吸收到非獨(dú)立變量u和獨(dú)立變量x,t的定義中,它們分別與物理系統(tǒng)中的距離和時(shí)間成正比時(shí),得到一類廣義的KdV方程如下:

對(duì)于上述方程,已有許多學(xué)者進(jìn)行了可積性與可解性相關(guān)的研究.文獻(xiàn)[16]研究了該方程的可積性,文獻(xiàn)[17-18]研究了廣義KdV方程的精確解及級(jí)數(shù)解等問題.通過適當(dāng)?shù)淖儞Q,方程(1)可轉(zhuǎn)化為一般的KdV方程,文中所得結(jié)論也可推導(dǎo)應(yīng)用于一般的KdV方程中.本文主要研究了廣義KdV方程(1)的留數(shù)對(duì)稱和CRE可解性,并基于此構(gòu)造出方程新的相互作用解,并作出相應(yīng)解的波形圖.

2 非局域留數(shù)對(duì)稱及其局域化

方程(1)的Painlev′e截?cái)嗾归_可表示為如下形式:

其中f表示奇異流形,u0,u1,u2,f都是關(guān)于x,t的函數(shù).將(2)式代入方程(1)中,令f的各次冪都為零,可解出

則有

同時(shí)f滿足下面的Schwarzian形式

其中

Schwarzian形式在M¨obious變換

下保持不變,即方程(5)容許如下的三個(gè)對(duì)稱:

其中c1,c2,c3為任意常數(shù).將表達(dá)式(3)代到方程(1)中,可以得到如下B¨acklund變換定理.

定理2.1(B¨acklund變換定理)如果f是方程(5)的解,則

是方程(1)關(guān)于f和解u之間的一個(gè)B¨acklund變換.當(dāng)f和u滿足B¨acklund變換(7)時(shí),方程(1)有如下的留數(shù)對(duì)稱:

由于非局域?qū)ΨQ不能直接約化,因此需要將其進(jìn)行局域化.為找到上述非局域留數(shù)對(duì)稱的有限對(duì)稱形式,首先需要解決如下初值問題:

其中ε是群參數(shù).由于在初值問題的求解中涉及函數(shù)以及它的導(dǎo)數(shù),需要對(duì)其進(jìn)行相應(yīng)的延拓將其轉(zhuǎn)換為局域的Lie點(diǎn)對(duì)稱.為此,引入輔助變量g和h,利用表達(dá)式

則方程(1)的非局域留數(shù)對(duì)稱可以被局域化為延拓系統(tǒng)(1),變換(7),表達(dá)式(10)的Lie點(diǎn)對(duì)稱,即

相應(yīng)的Lie點(diǎn)對(duì)稱的向量場(chǎng)表達(dá)式為

由Lie的第一基本定理,得到如下初值問題:

解上面的初值問題便可得到下面的對(duì)稱群變換定理.

定理2.2(對(duì)稱群變換定理)如果f,g,h,u是系統(tǒng)(1),變換(7),表達(dá)式(10)的解,則也是,其中

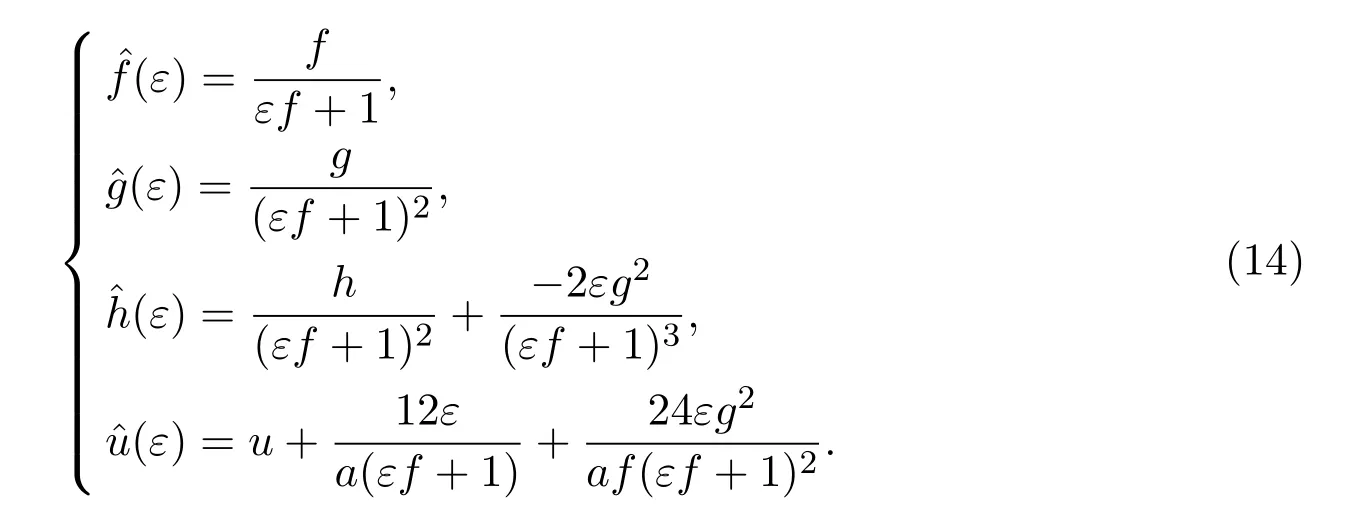
3 CRE可解性及新的精確解

根據(jù)CRE方法,方程(1)有如下形式的截?cái)嗾归_式:

其中w=w(x,t),R(w)是Riccati方程

的解,l0,l1,l2是任意常數(shù),且l20.將表達(dá)式(15)和方程(16)代入方程(1)中,令R(w)的各次冪前面的系數(shù)為零,可解出

同時(shí),w滿足方程

其中

由此可知,方程(1)也是CRE可解的.因此,得到如下定理.

定理3.1(CRE可解性定理)如果w是方程(18)的一個(gè)解,則

也是方程(1)的解,其中R(w)是Riccati方程的解,且u0,u1,u2滿足(17)式.

注3.1當(dāng)l0=1,l1=0,l2=-1時(shí)Riccati方程(16)有一個(gè)特解為

此時(shí),稱該系統(tǒng)為CTE可解系統(tǒng),截?cái)嗾归_式(15)變?yōu)?/p>

根據(jù)文獻(xiàn)[3],方程(18)的解描述了方程(1)的孤立子和其它非線性激發(fā)的相互作用解,設(shè)其一般形式為

將(22)式代入方程(18),得到下面的橢圓方程:

其中

因此,方程(1)的解具有如下形式:

其中R(w)是Riccati方程的解,且有

接下來討論方程(1)的孤立波與橢圓周期波之間的兩種特殊形式的相互作用解.

例3.1取橢圓方程(23)的解W為如下特殊形式:

其中sn(k2x+h2t,m)為橢圓函數(shù),Eπ為第三類不完全橢圓積分.取

此時(shí)Riccati方程的解為

將(26)式-(27)式代入(25)式中,可以得到方程(1)的相互作用解

其中

利用主項(xiàng)分析計(jì)算,能夠得到c,k2,h2需滿足如下關(guān)系式:

圖1為例3.1中方程(1)的相互作用解u的波形圖,圖2為t=0時(shí)例3.1中解u的平面周期波結(jié)構(gòu)圖,參數(shù)選擇如下:

圖1 u的波形圖

圖2 t=0時(shí)u的平面波結(jié)構(gòu)圖

顯示出孤立波在橢圓周期波作用下的傳播.

例3.2取橢圓方程(23)的解W為如下形式:

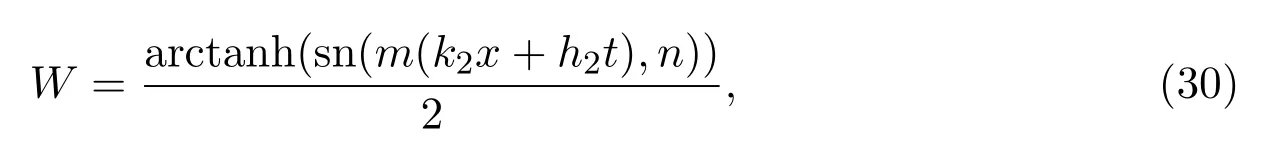
其中sn(m(k2x+h2t),n)為橢圓函數(shù).取l0=l1=0,l2=1,此時(shí)Riccati方程的解為

將(30)式-(31)式代入(25)式中,可以得到方程(1)的相互作用解為

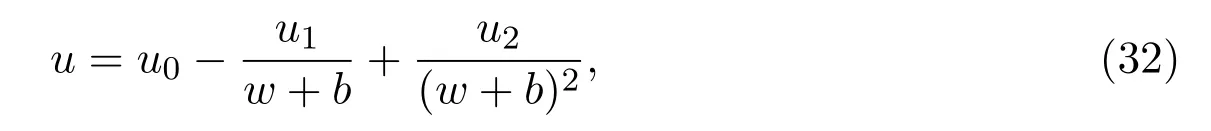
其中

通過計(jì)算,k2,h2需滿足如下關(guān)系式:

圖3為例3.2中方程(1)的相互作用解u的波形圖,圖4為t=0時(shí)例2中解u的平面波結(jié)構(gòu)圖,參數(shù)選擇如下:{a=2,b=3,m=1,n=1,C2=3,h1=2,k1=1},顯示出鐘狀孤立波的傳播.

圖3 u的波形圖

圖4 t=0時(shí)u的平面波結(jié)構(gòu)圖

4 結(jié)束語

由Painlev′e截?cái)嗾归_法得到廣義KdV方程的留數(shù)對(duì)稱和B¨acklund變換定理,并通過引入合適的新變?cè)獙⑵渚钟蚧癁長ie點(diǎn)對(duì)稱,在此基礎(chǔ)上,利用Lie的第一基本定理研究了延拓系統(tǒng)的有限變換.最后,用CRE方法獲得了該方程的新的相互作用解.為了更好地研究解的性質(zhì),通過選取適當(dāng)?shù)膮?shù),利用Maple軟件給出了解的相應(yīng)圖形,進(jìn)而可以更好地分析其解的性質(zhì)以及波峰波谷的形狀.