一類帶對數(shù)非線性源項的p-Laplace拋物方程解的存在性與爆破
溫蘭, 楊晗
( 西南交通大學數(shù)學學院, 四川成都 611756)
1.引言
本文研究如下帶對數(shù)非線性源項的p-Laplace拋物方程的初邊值問題
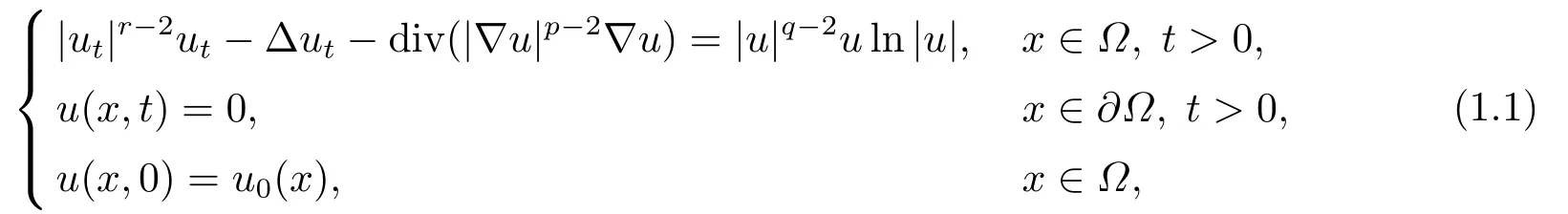
其中r >1, p>2, q >2,u0(x)∈(?),?是Rn(n ≥1)中具有光滑邊界?? 的有界區(qū)域.當方程(1.1)中r =2, p=2時, XU和SU[1]研究如下半線性偽拋物方程的初邊值問題:
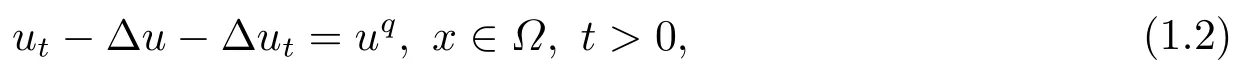
利用勢井方法得出方程整體解的存在性并得到解在有限時刻的爆破.近年來, 含對數(shù)非線性源項的拋物方程已引起大量學者的研究.CHEN等[2]中研究了帶對數(shù)非線性源項的偽拋物方程初邊值問題:
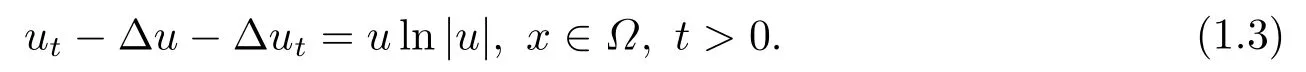
因對數(shù)非線性u ln|u|不滿足Payne和Sattinger[3]中提出的多項式增長條件, 此時經(jīng)典勢井方法不完全適用.文[2]通過勢井方法及對數(shù)索伯列夫不等式證明方程整體解的存在性, 并用凸方法證明解在無窮時刻爆破.通過比較得出多項式非線性項對此類偽拋物方程解在有限時刻的爆破有更為重要的影響.隨后, 文[4-5]中將上述帶對數(shù)非線性源項的方程拓展到p-Laplace情形.LE等[5]中研究了如下含對數(shù)非線性源項的p-Laplace偽拋物方程的初邊值問題:
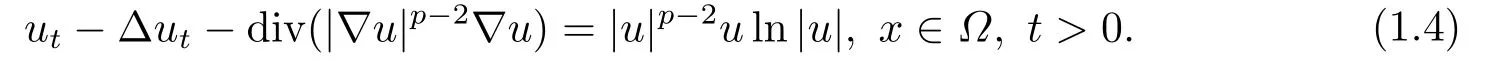
利用勢井方法及對數(shù)索伯列夫不等式證明了當p > 2時方程整體解的存在性, 并用凸方法得出此時解在有限時刻的爆破.而CAO等[6]中利用Galerkin方法證明了當1 < p < 2時方程整體解的存在性并得出此時解在無窮時刻的爆破.當p-Laplace項與對數(shù)非線性項的指數(shù)不同時, 對數(shù)索伯列夫不等式不再完全適用.文[7-9]中主要研究下述帶對數(shù)非線性源項的p-Laplace偽拋物方程的初邊值問題:
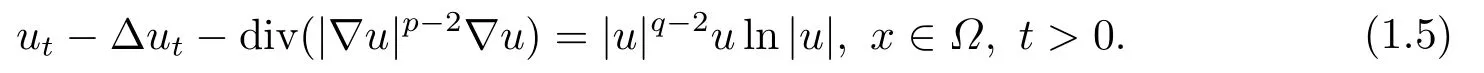
HE等[7]用Galerkin方法證明當2 < p < q < p(1+)時, 方程局部弱解的存在唯一性, 并結合勢井方法證明了方程整體解的存在性, 最后得出解的(?)范數(shù)在有限時刻的爆破.而DAI等[8]對上述結果進行推廣主要得出在不同的初始能量下弱解在有限時刻爆破的上界及下界.
對于擬線性情形, Pucci和Serrin[10]中研究如下方程的初邊值問題,
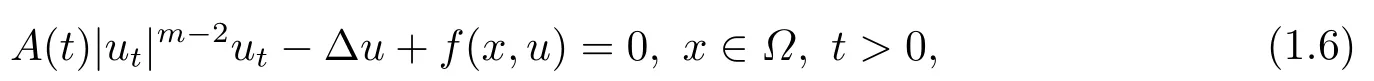
其中m > 1, A ∈C(J →RN×N), f ∈C(?×RN→RN)且滿足(f(x,u),u) ≥0, 得出方程強解的整體存在性和當t →∞時強解的漸近穩(wěn)定性.當上述方程(1.6)中f(x,u) = ?|u|p?2u時,PANG等[11]中用Galerkin方法證明了當p > 2時初值在穩(wěn)定集中時方程整體解的存在性, 再通過構造輔助泛函得出當1 基于上述結論, 本文研究方程(1.1)初邊值問題, 主要考慮非線性項指數(shù)之間的競爭與?ut項對方程解的存在性和爆破的影響.首先用Galerkin方法證明當非線性項指數(shù)滿足適當條件時方程局部解的存在性; 然后結合勢井方法證明初值在穩(wěn)定集中時方程整體解的存在性;最后通過構造輔助泛函證明解在有限時刻的爆破. 本文結構安排如下: 第二部分介紹一些符號和引理; 第三部分給出局部解和整體解存在性; 第四部分證明解在有限時刻爆破. 其中N代表Nehari流形, d為勢井深度.類似文[7]中引理1和引理2證明可知: 集合N非空, 常數(shù)d存在且大于0.由(2.5)和(2.6)可得 定義以下穩(wěn)定集和非穩(wěn)定集 下面給出證明過程所需引理, 詳細證明過程可參考文[9]. 成立, 則稱u 在有限時刻爆破. 這節(jié)將給出當非線性項指數(shù)滿足適當條件時方程(1.1)局部解和整體解的存在性. 由(3.14)-(3.16), 存在T >0, ?t ∈[0,T]有 由引理2.5并結合(3.17)可得 由此可得 結合(3.25), (3.29)可得χ1=|u|q?2u ln|u|. 設Au = ?div(|?u|p?2?u), 易證A為嚴格單調半連續(xù)有界的強制性算子(可參考文[12]).則由(3.27)結合單調算子理論可得 由gjm(0)=ξjm, 當m →∞時, u0m強收斂到u0, 因此有 則對于充分大的m, 有 由此可得, 對于充分大的m, um(0)∈W. 下證對于充分大的m, ?t ∈[0,T], 有um(t)∈W成立. 若不成立, 則存在t0∈[0,T]使得um(t0) ∈?W, 此時有um(t0) ∈(?), 且J(um(t0)) =d或I(um(t0)) = 0.若J(um(t0)) = d, 而由(3.43)得J(um(t0)) < d, 矛盾; 若I(um(t0)) = 0,此時um(t0) ∈N, 由d的定義可得J(um(t0)) ≥d, 顯然與(3.43)矛盾.故對于充分大的m,?t ∈[0,T], 有um(t)∈W成立. 因um(t)∈W, 有I(um)>0, 結合方程(2.5)和(3.43), 對于充分大的m, 有 由此可得 對于任意T >0, t ∈[0,T]成立.再結合定理3.1的證明, 定理3.2得證. 將方程(1.1)兩邊同乘以u,并在?上對x積分,因I(u)<0,結合(2.5)和引理2.3,由Hlder不等式及Young可得 令ε充分小有 注4.1對于J(u0) < 0情形, 在(4.1)中令H(t) = ?J(t)同樣可得出解的(?)范數(shù)在有限時刻的爆破, 證明過程大致同上, 在此省略.2.準備工作

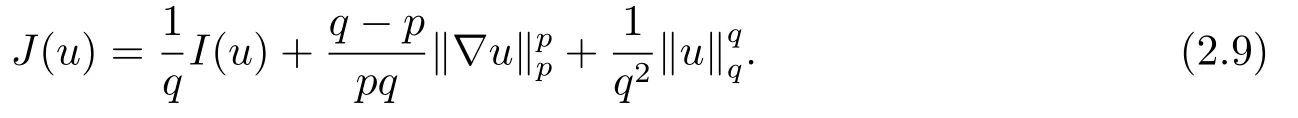
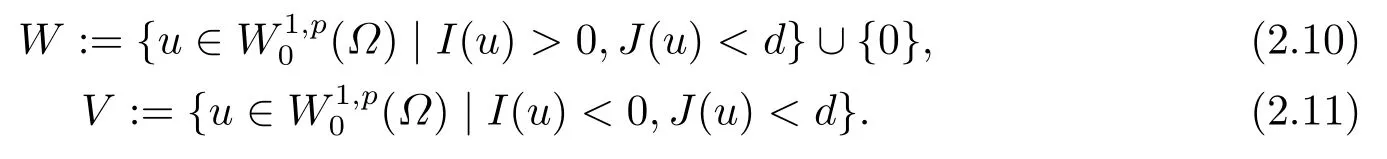

3.解的存在性





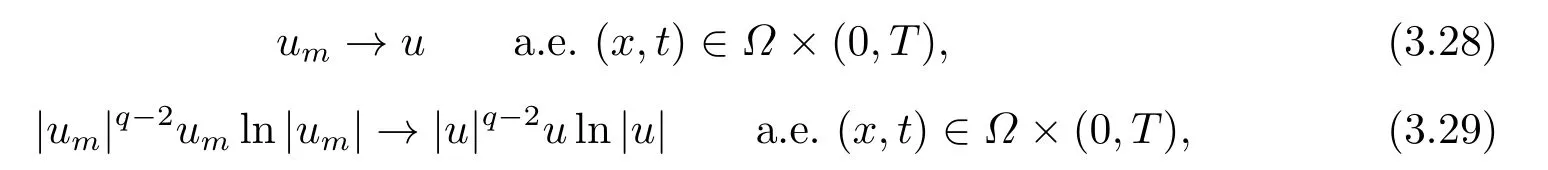

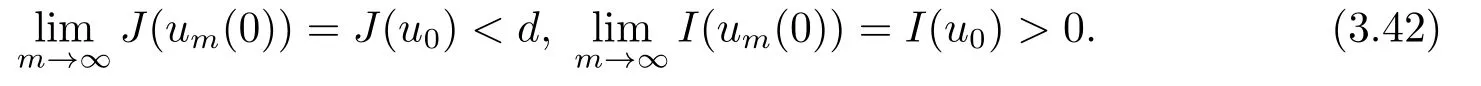
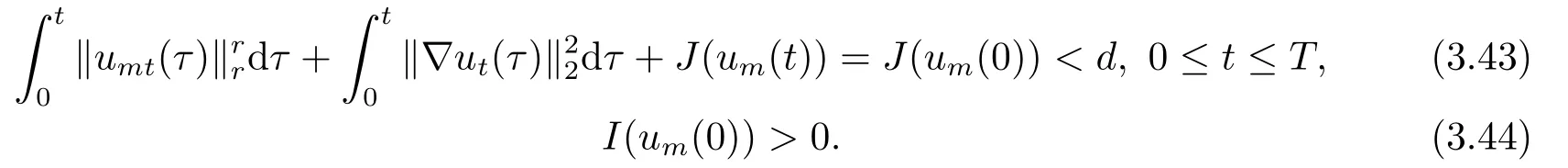
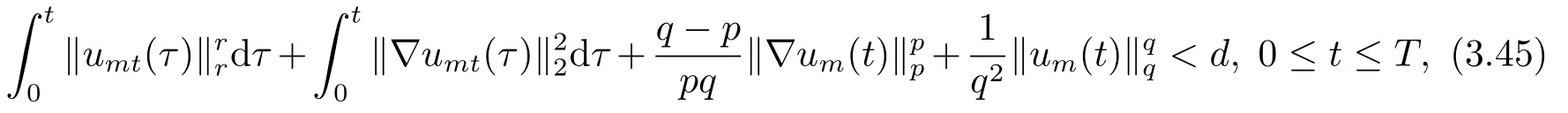

4.爆破