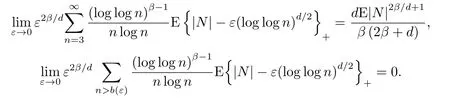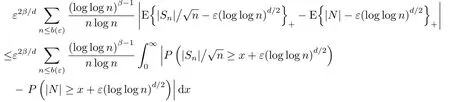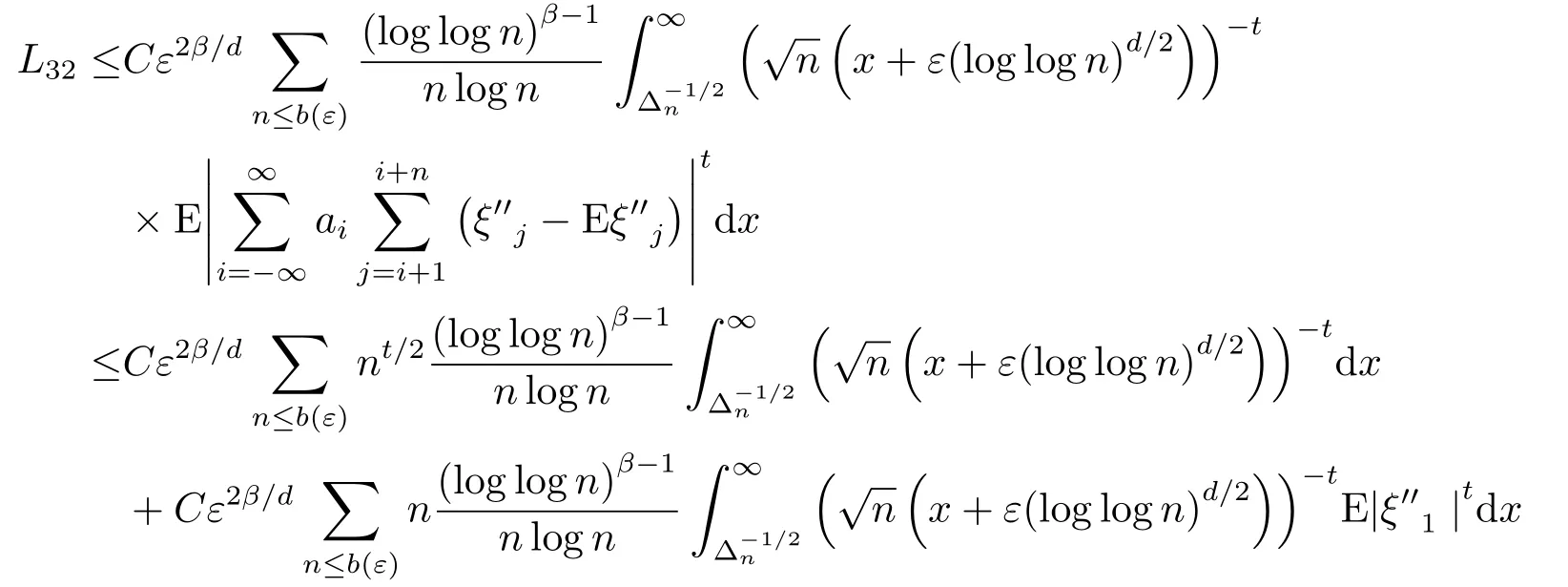ρ-混合序列移動平均過程的完全矩收斂
費丹丹, 付宗魁, 黃瓊敖
(1.信陽學院數(shù)學與統(tǒng)計學院, 河南信陽 464000;2.華南師范大學華南數(shù)學應用與交叉研究中心, 廣東廣州 510631)
1.引言及主要結(jié)果
雙側(cè)無窮混合序列的概念首先由Kolmogorov和Rozanov[1]提出, 即:
定義1.1[1]設{Yi,?∞ 如果ρ(n)→0,n →∞.則稱序列{Yi,?∞ 由于ρ-混合序列是比獨立序列和φ-混合序列適用范圍更廣泛的隨機變量序列, 因此對ρ-混合序列的概率極限理論的研究是非常必要的.目前已得到許多關(guān)于ρ-混合序列的研究成果.[2?5]完全收斂性的概念由Hsu和Robbins[6]首先提出, Chow[7]對其深入研究得到了完全矩收斂, 這些已引起許多學者的關(guān)注, 得到了一系列獨立和混合相依序列的結(jié)果, 見文[8-12].最近,FU等[8]得到了NA(negatively associated)序列對數(shù)律的完全矩收斂, 即: 其中N為標準正態(tài)隨機變量. 隨后, XIAO等[9]將定理1.1的結(jié)果改進, 得到了獨立序列重對數(shù)律的一階矩收斂的精確漸近性.即: 其中N為標準正態(tài)隨機變量. 設{ξi,?∞<ξi<∞}為雙側(cè)無窮隨機變量序列, {ai,?∞ 是基于{ξi,?∞<ξi<∞}的移動平均過程, 記為式(1.1)的部分和. 對隨機變量序列移動平均過程的極限理論已獲得了一系列重要結(jié)果, 尤其是完全收斂性的研究.若{ξi,?∞<ξi<∞}為獨立同分布序列時, 見文[13-15].若{ξi,?∞<ξi<∞}為混合序列時, 見文[16-18].但關(guān)于混合序列移動平均過程的完全矩收斂的研究成果很少, 本文是將定理1.1和定理1.2的結(jié)果推廣到ρ-混合序列移動平均過程. 在整篇文章中, C在不同的位置表示不同的常數(shù), I(A)表示集合A的示性函數(shù), log x =ln max(x,e), x+=max(x,0), [x]表示不大于x的最大整數(shù), ?→表示依分布收斂.本文的主要結(jié)果如下: 不失一般性, 設τ = 1.令a(ε)=exp(Mε?1/q), M >4, 0<ε <1/4.定理1.3可由以下四個命題得證. 命題3.1對q ≥1/2及b>q ?1, 則 證容易得到 故命題3.1成立. 命題3.2對q ≥1/2及b>q ?1, 則 證取λ>由Markov不等式得 于是, 由(3.7)和(3.9)知(3.3)成立, 命題3.3得證. 命題3.4在定理1.3的條件下, 則 首先, 估計H1, 由Toeplitz引理知 其次, 估計H2, 由Markov不等式和Toeplitz引理知 最后, 估計H3, 對充分大的n, 由x>和(3.4)知 于是, 由(3.14)知 對H32, 由Markov不等式, (3.8)和E|ξ1|t<∞, t ≥2, 知 因此, 由(3.16)和(3.17)知(3.10)成立, 命題3.4成立. 不失一般性, 設τ = 1.令b(ε) = exp(exp(Mε?2/d)), M > 1, 0 < ε < 1.定理1.4可由以下三個命題得證. 命題4.1[9]對d>0和β >0,則 命題4.2在定理1.4的條件下, 則 證與命題3.3中的記號?n一樣, 則 類似命題4.3中H31的證明知 下面估計L32由Markov不等式, t ≥2, (3.8)和E|ξ1|2<∞知 類似命題3.3中I1和I2的證明知K1→0, K2→0, M →∞.因此, 命題4.3成立.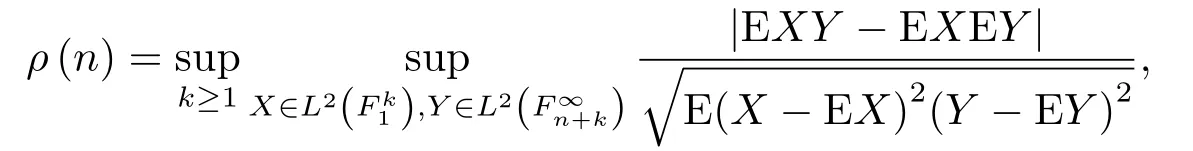
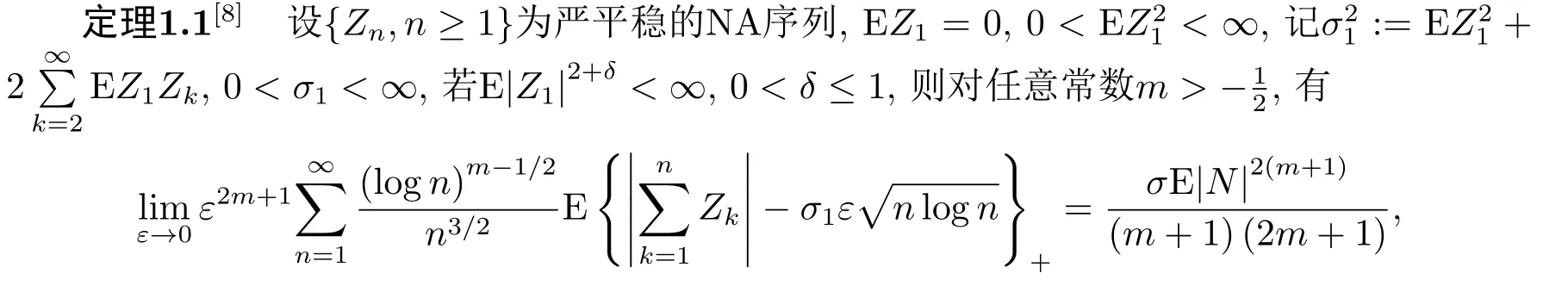
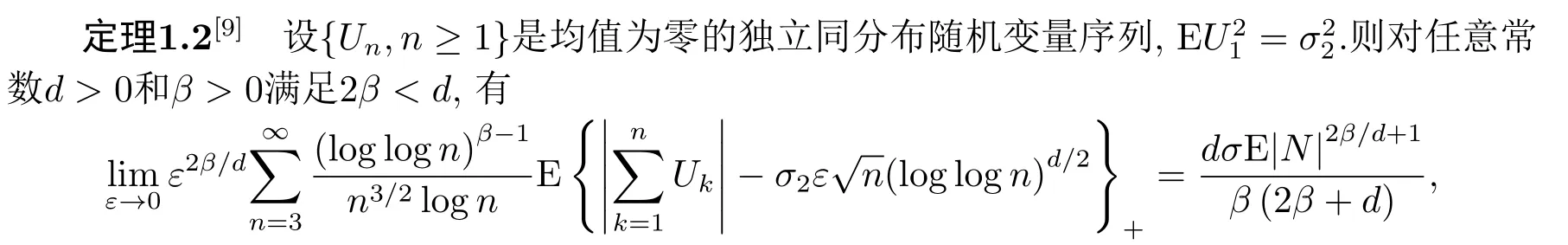


2.引理

3.定理1.3的證明
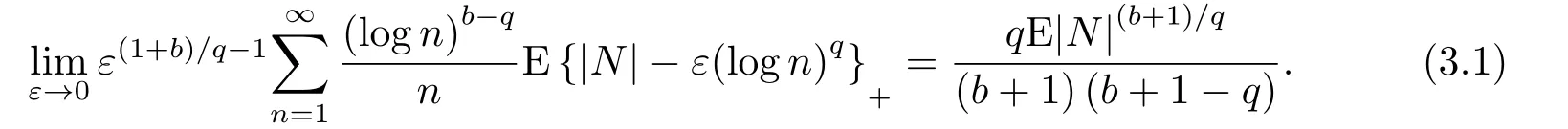
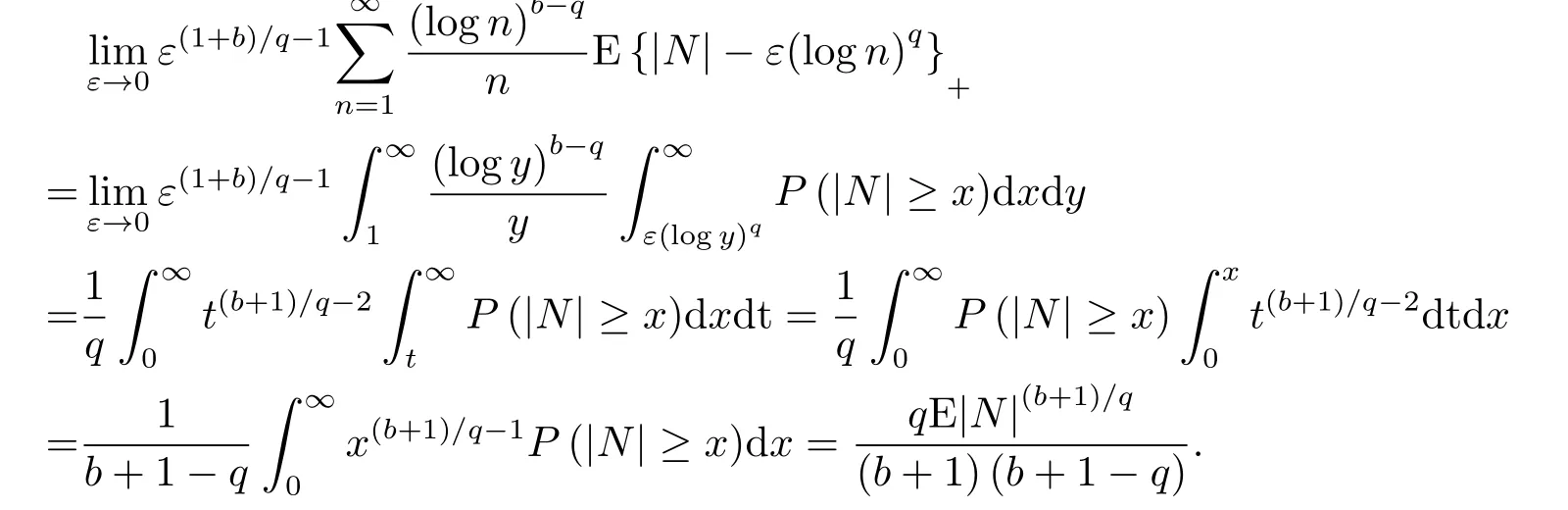
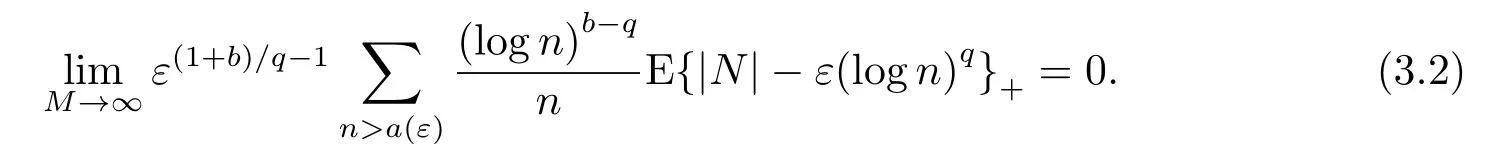




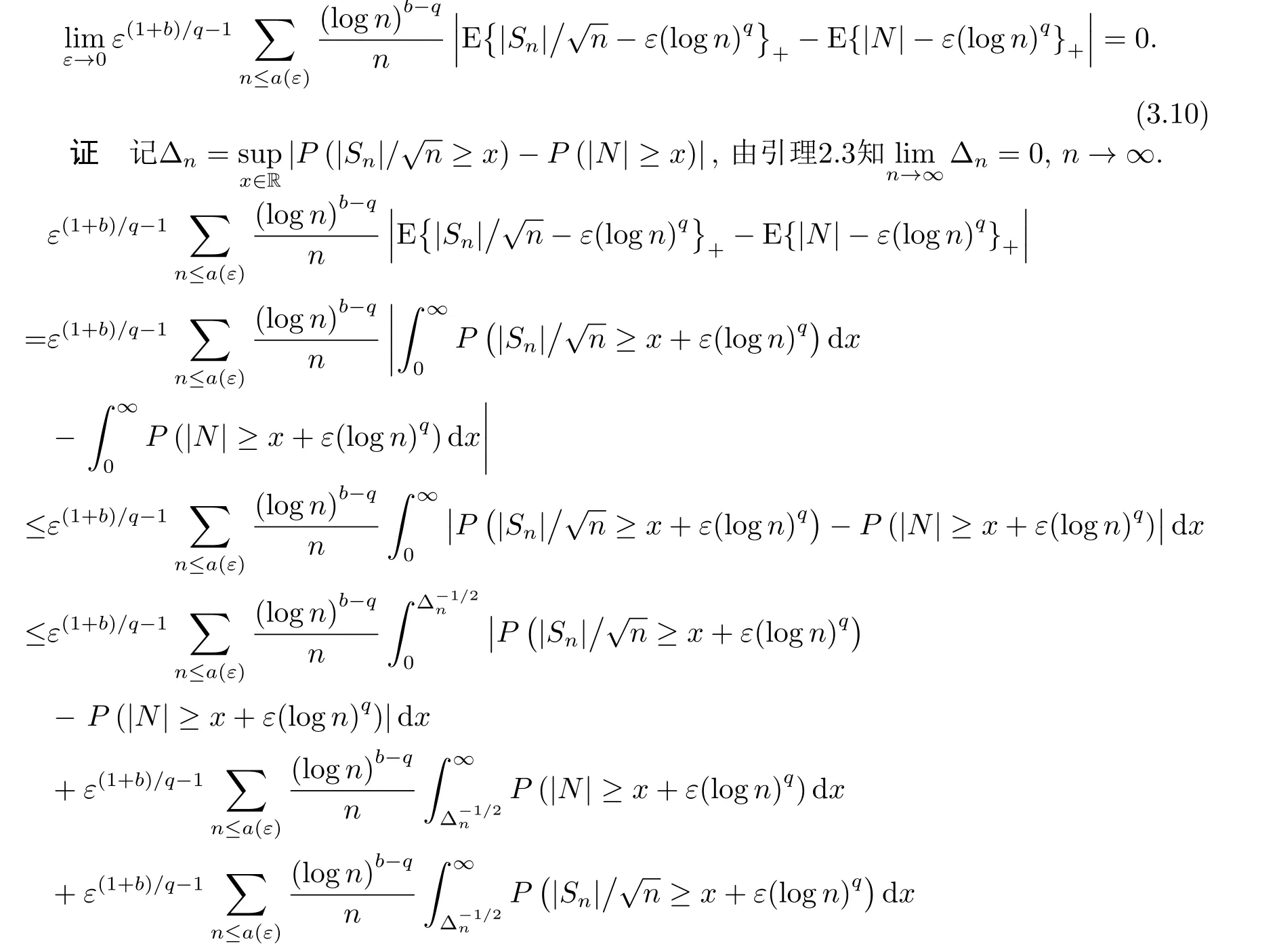

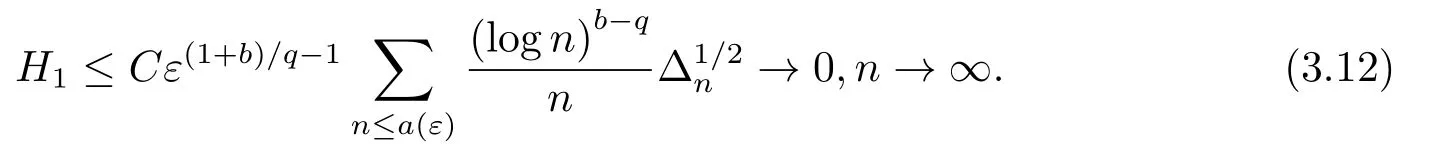
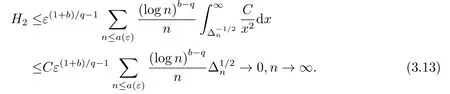
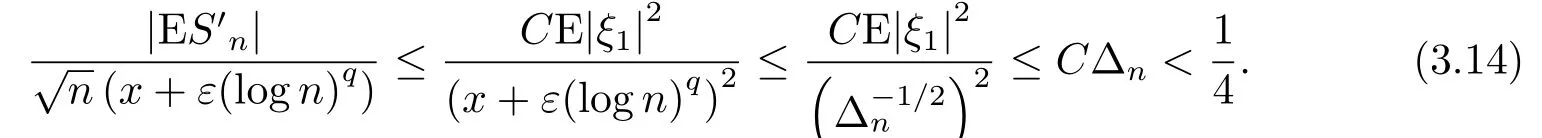

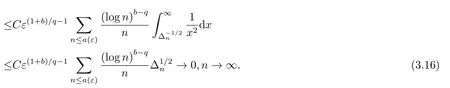

4.定理1.4的證明