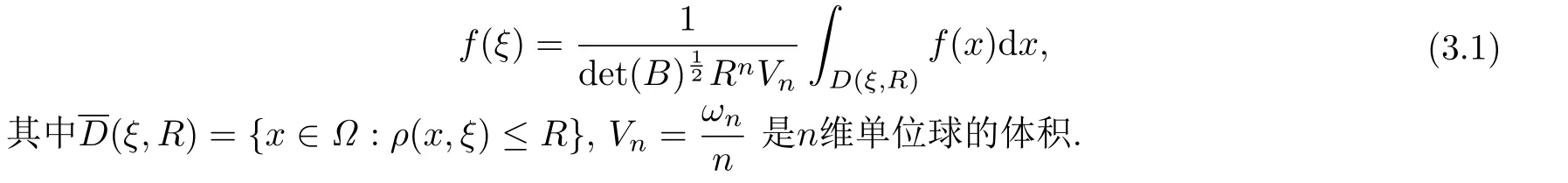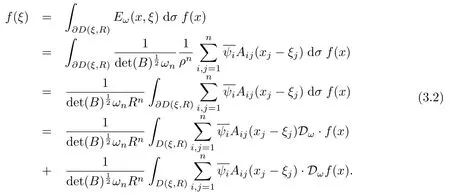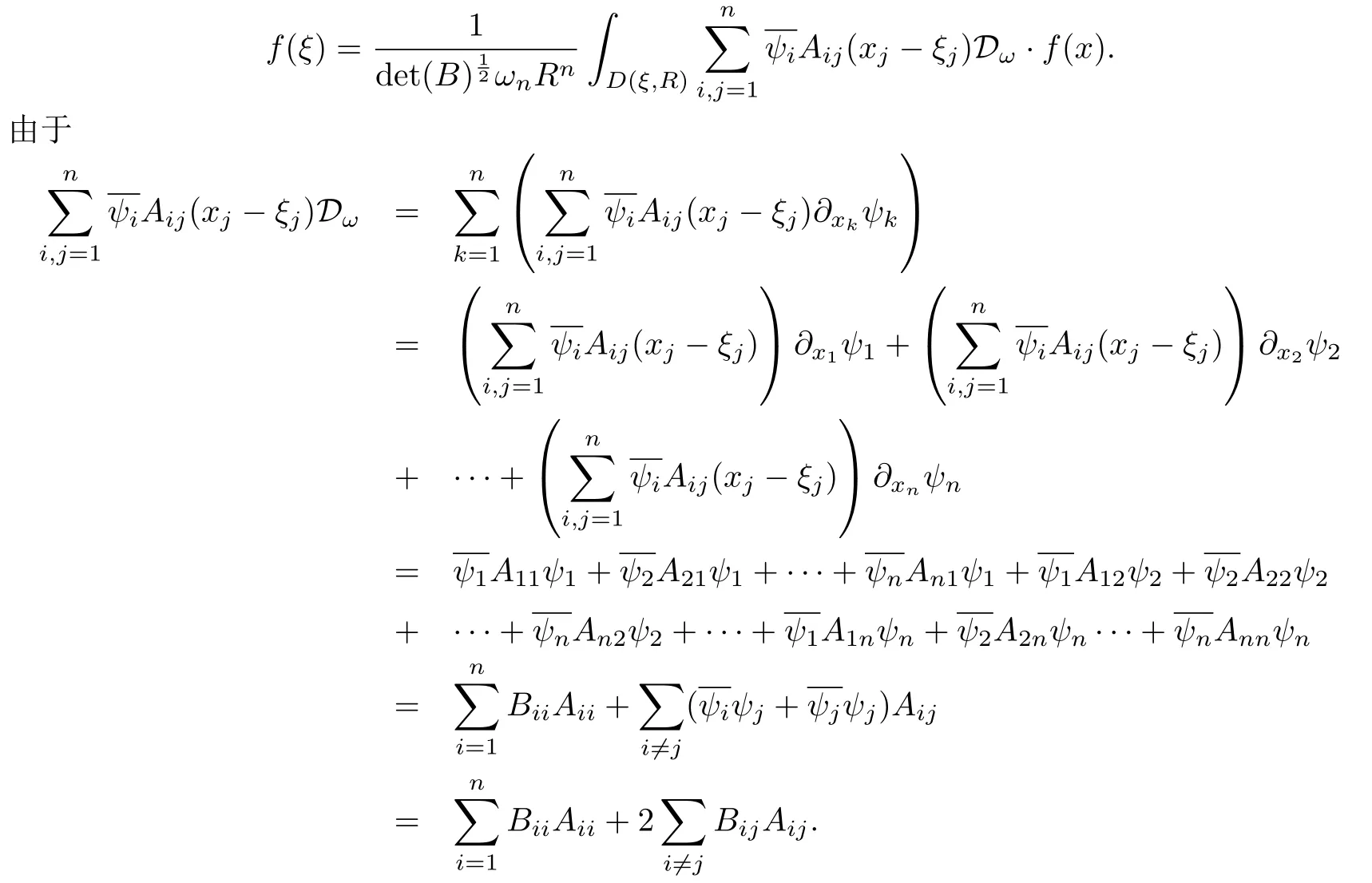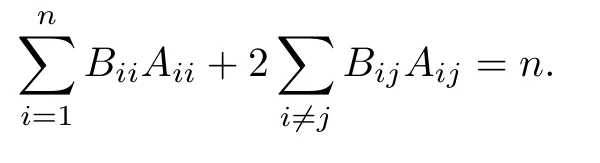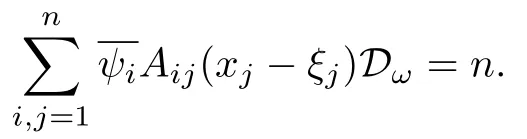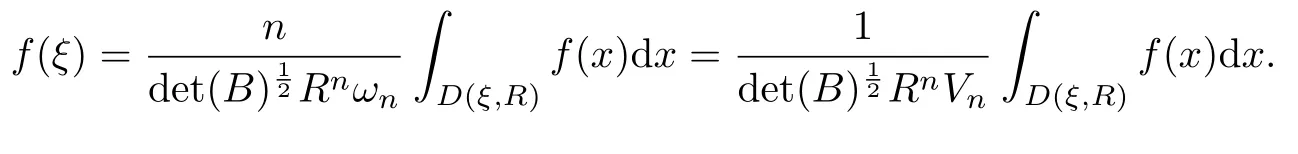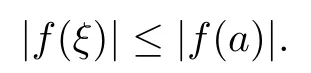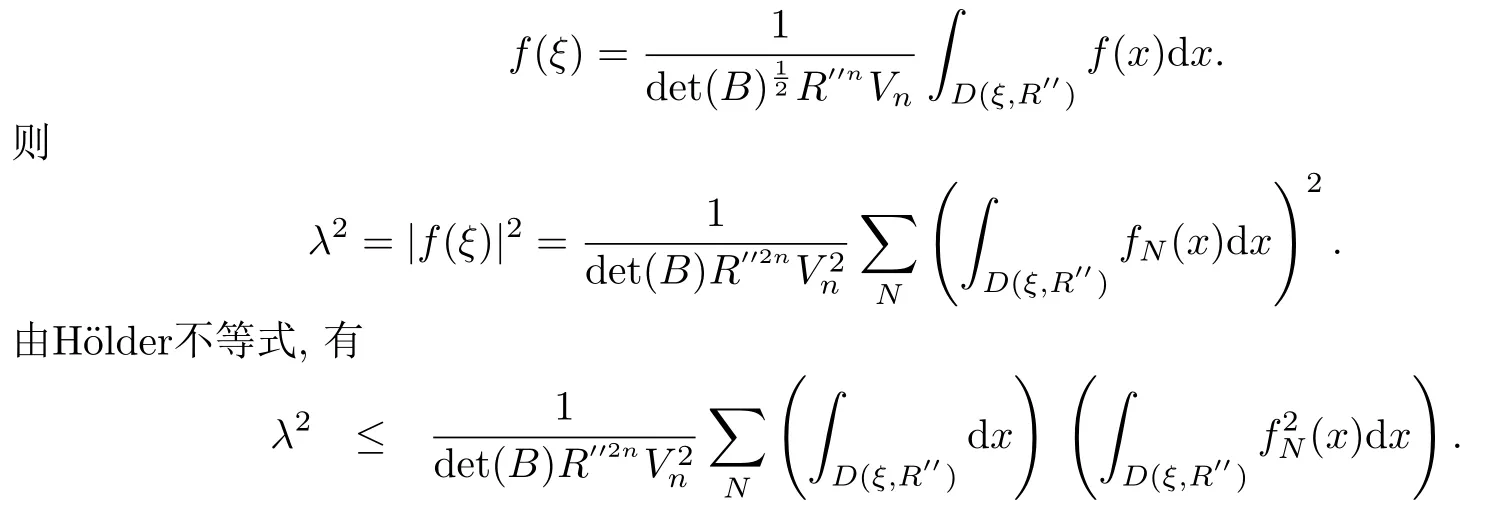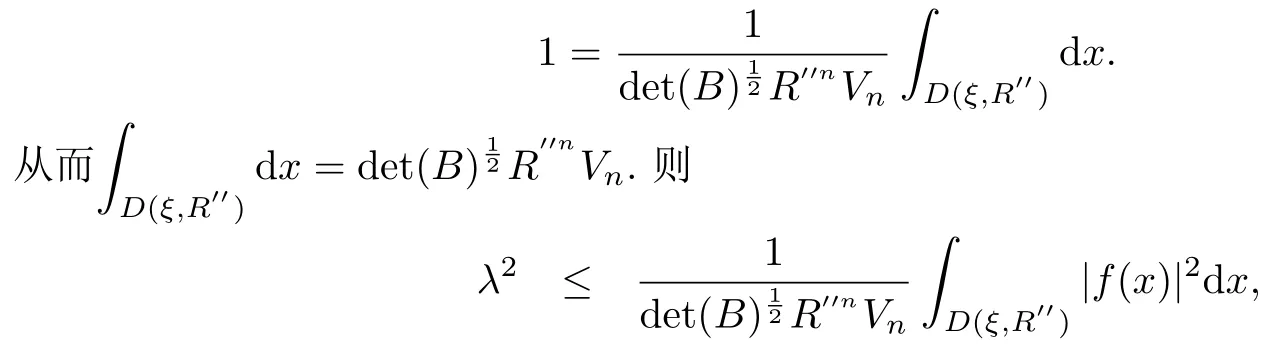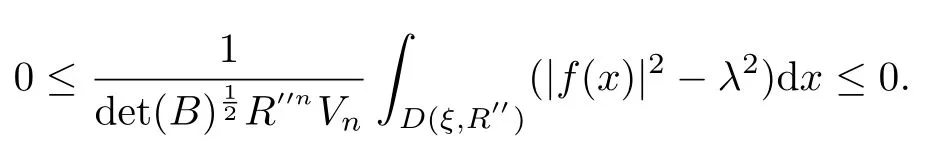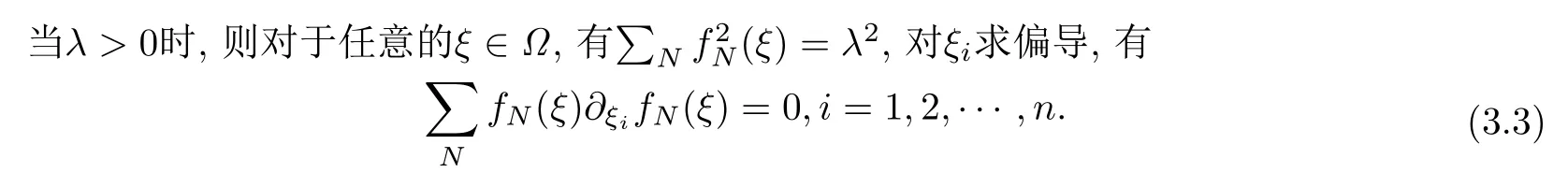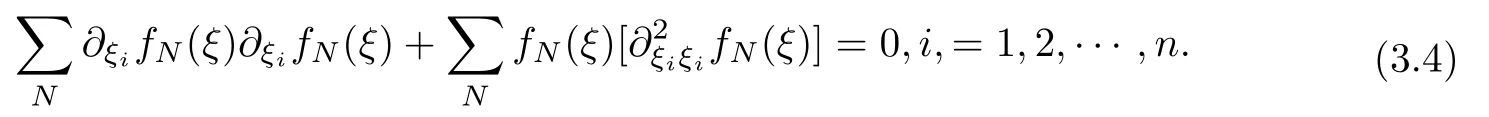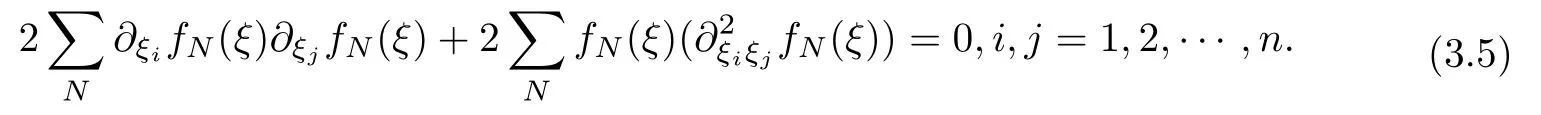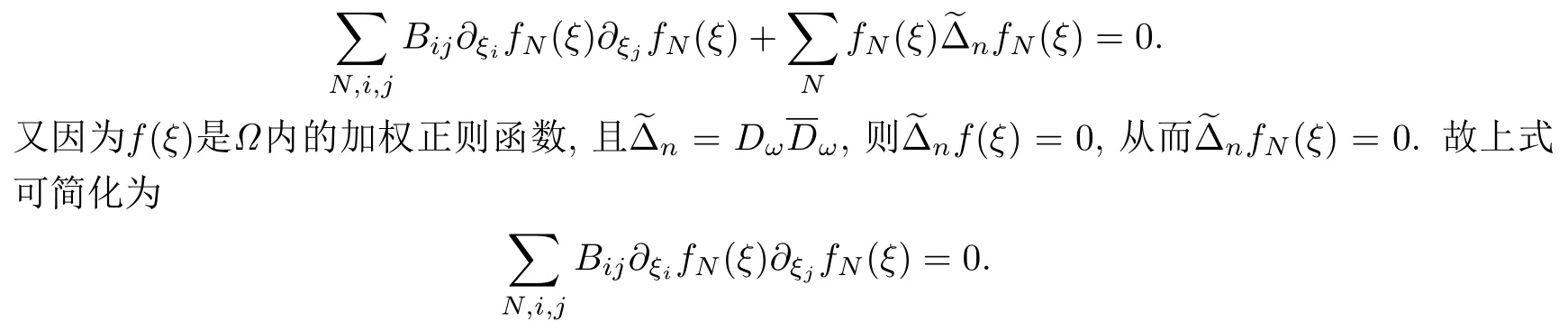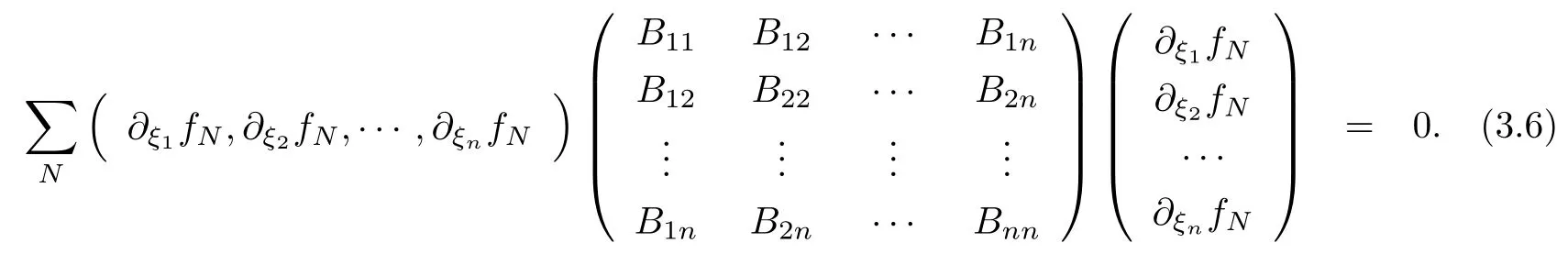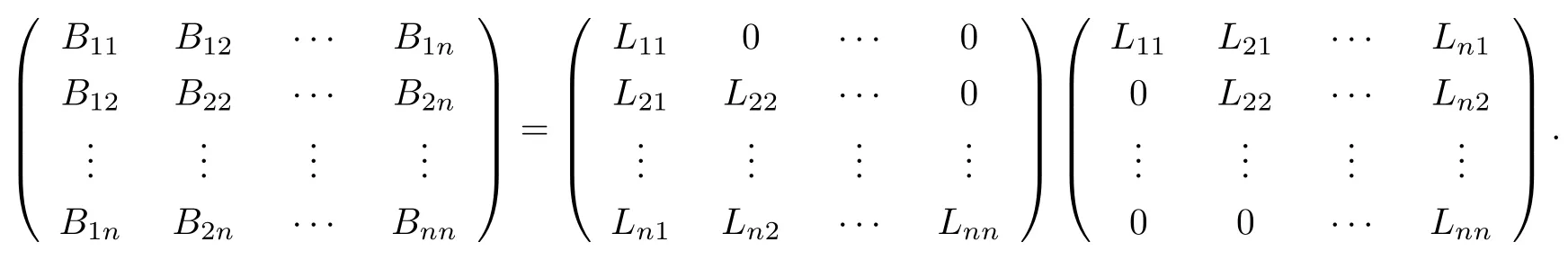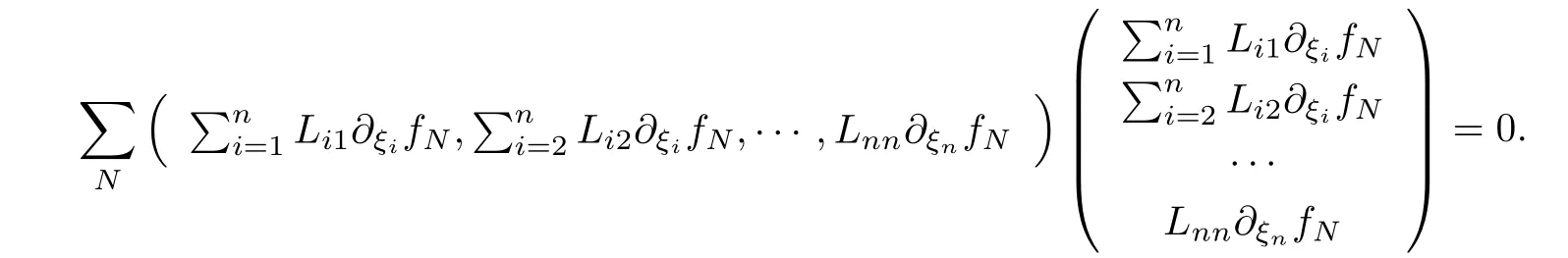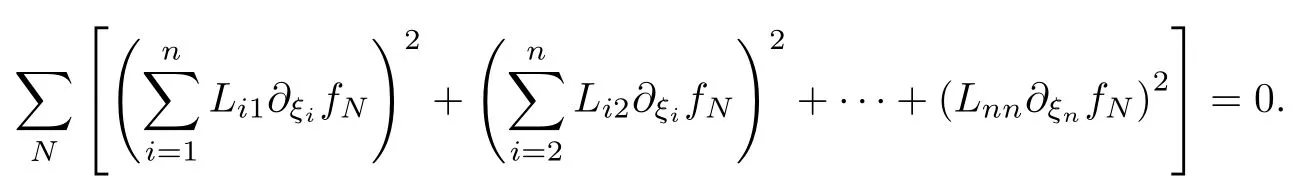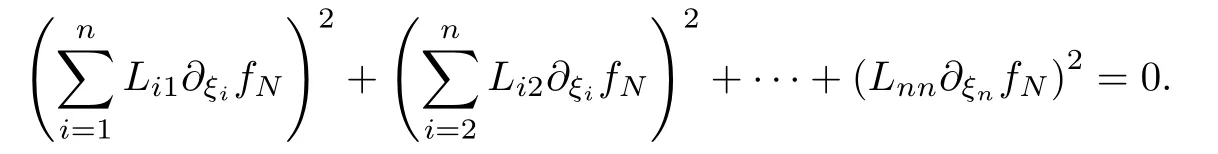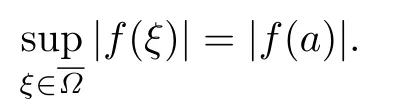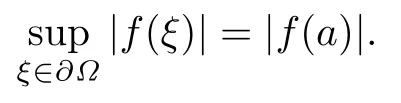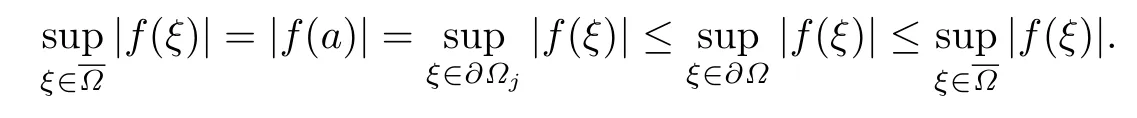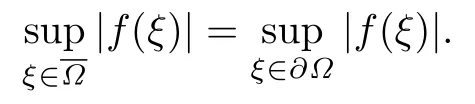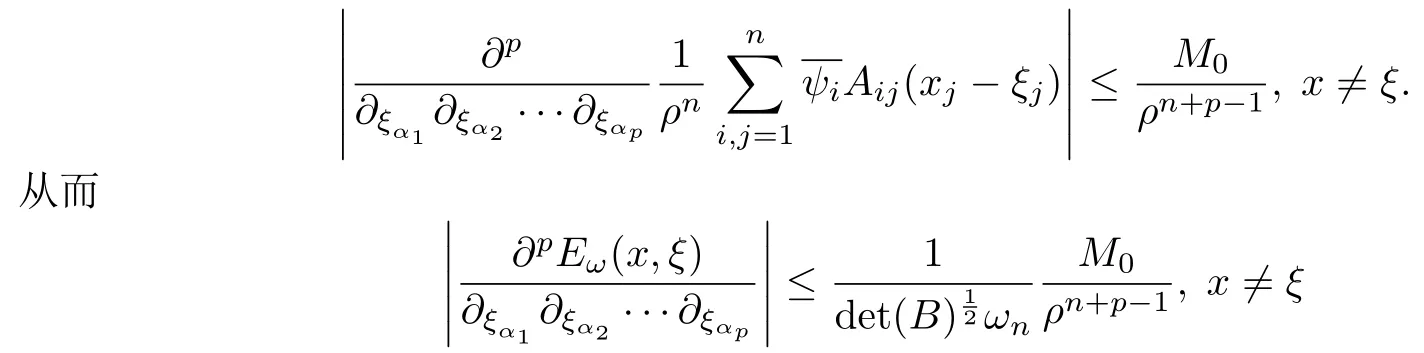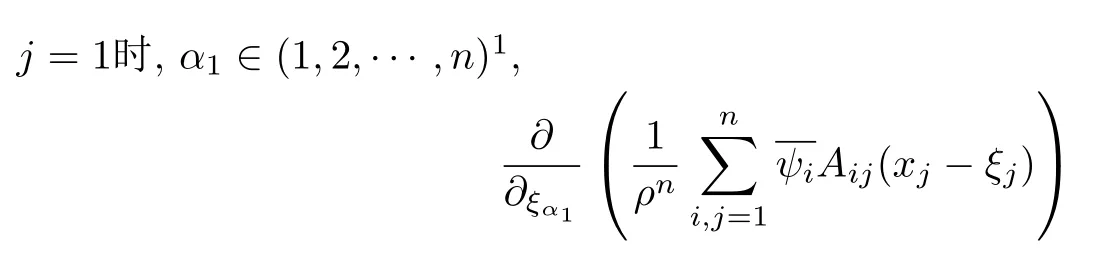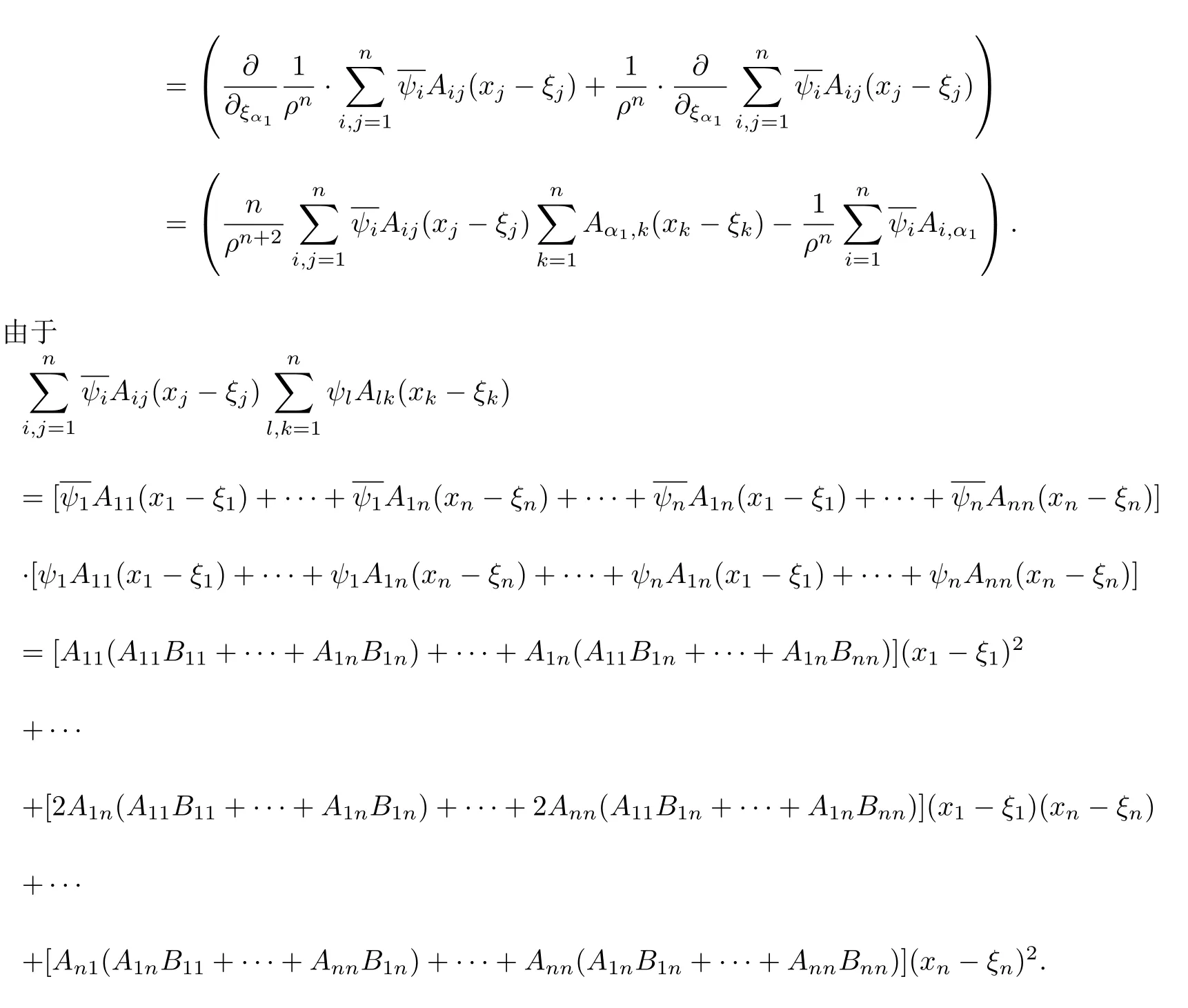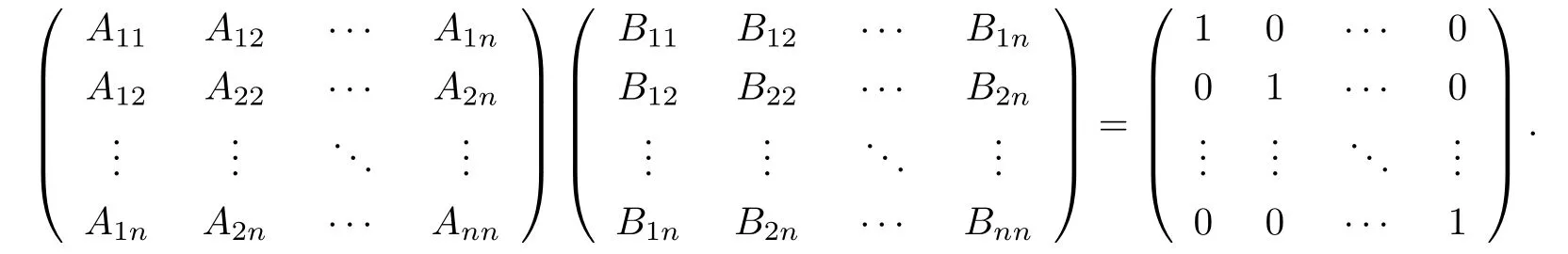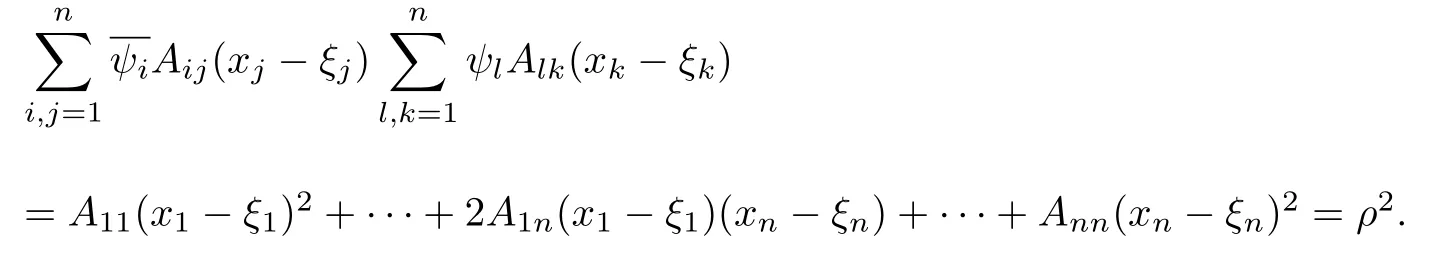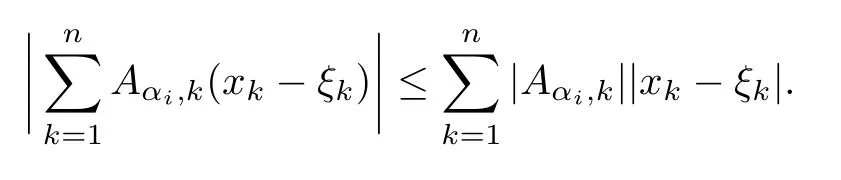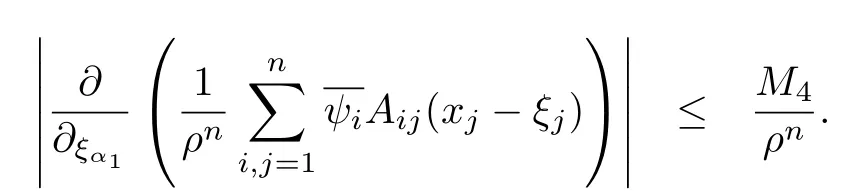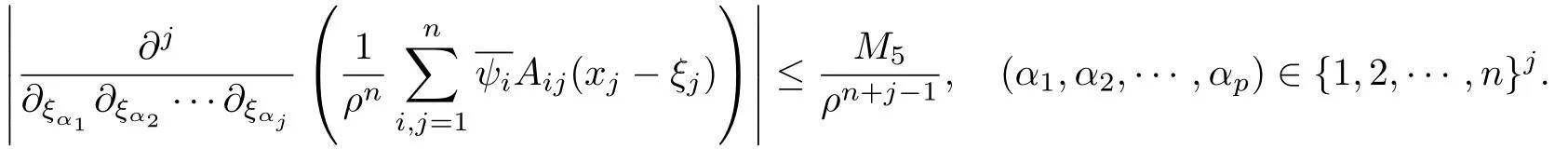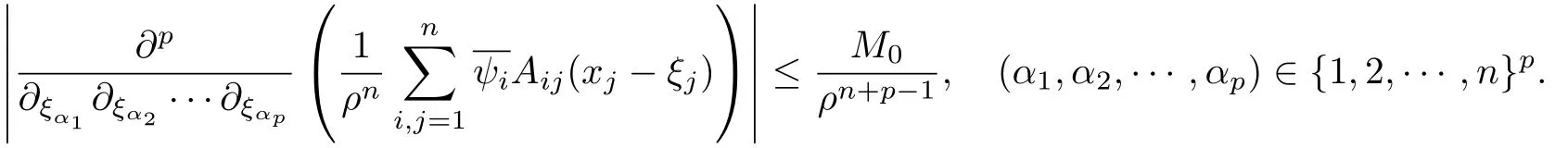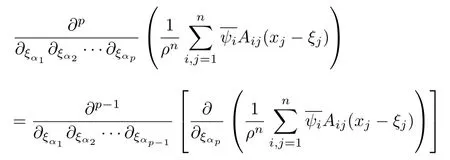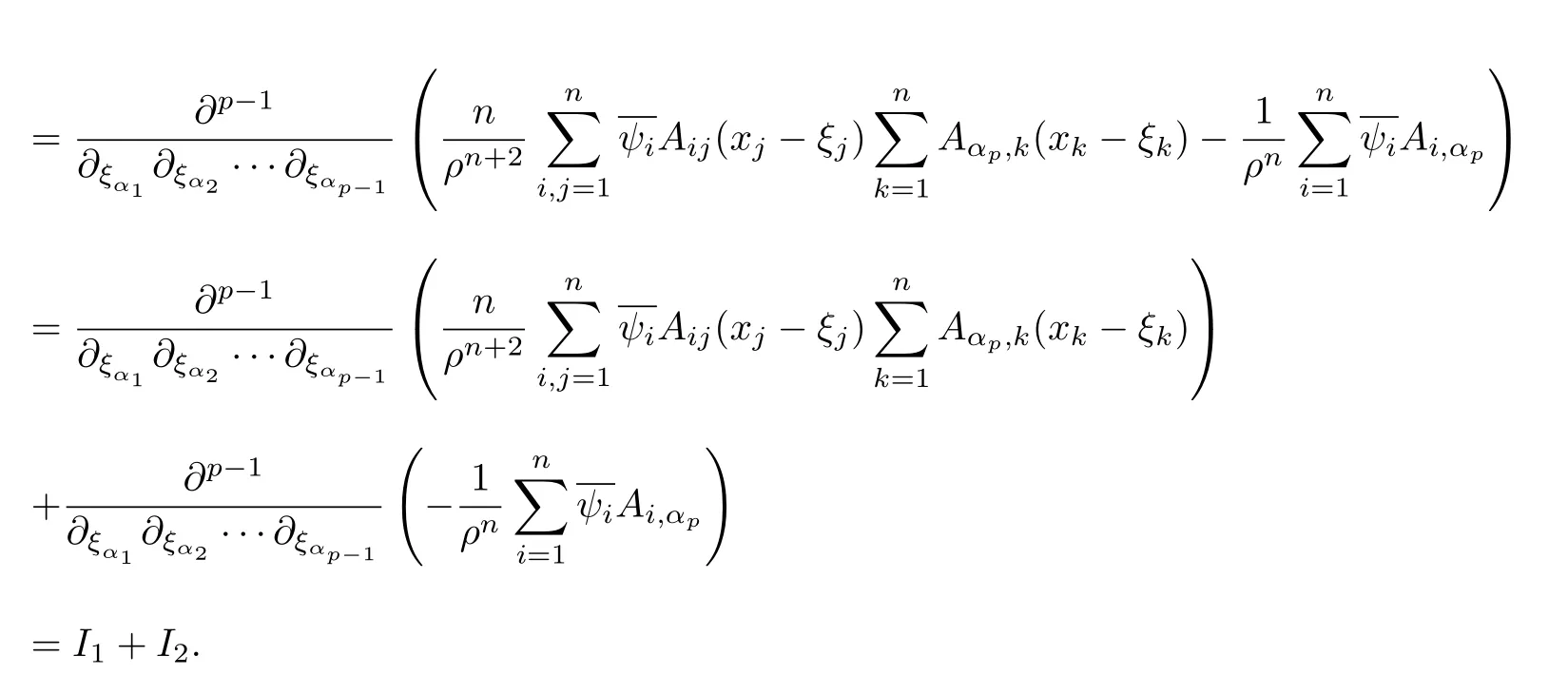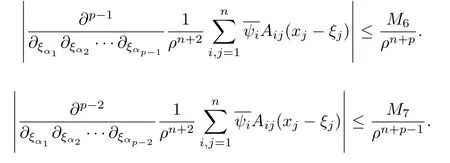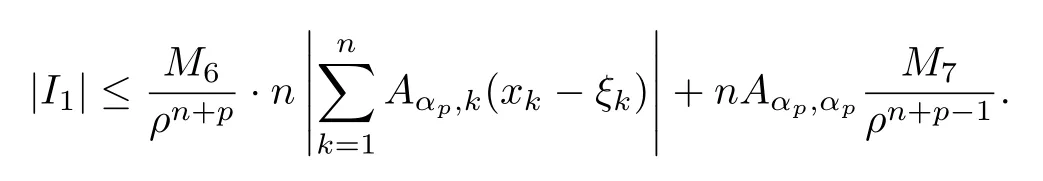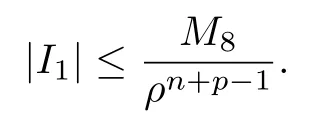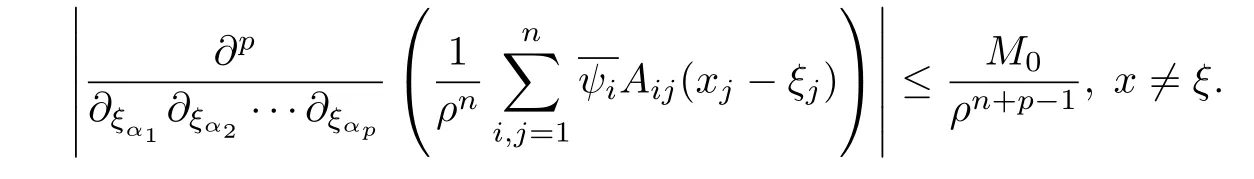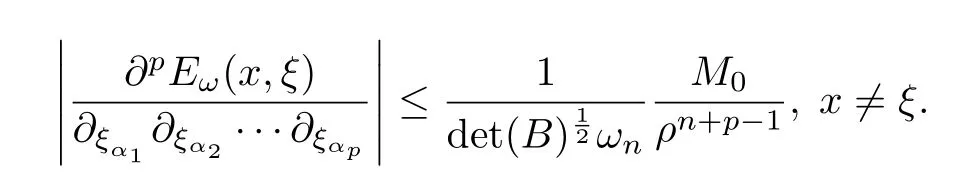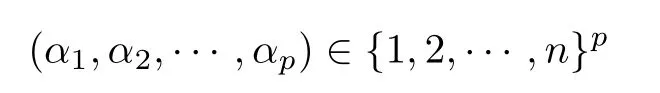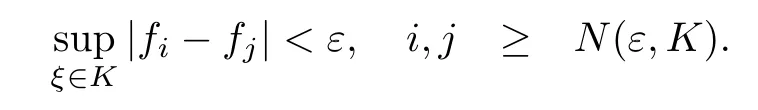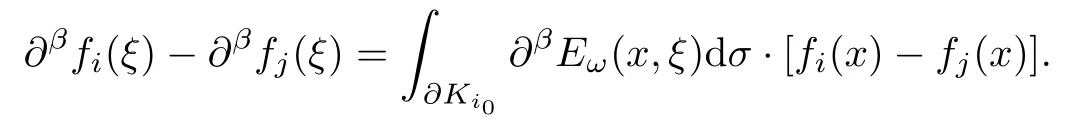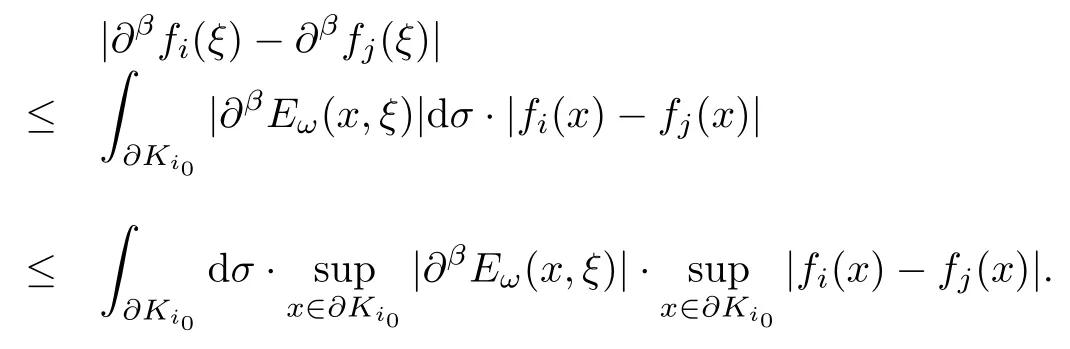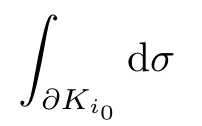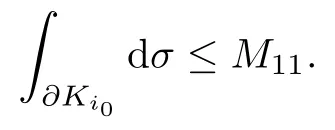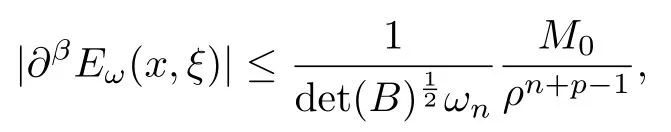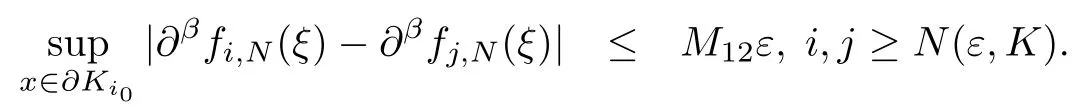加權(quán)正則函數(shù)的一些性質(zhì)
羅利萍,王麗萍,邱 芬
(河北師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院,河北石家莊 050024)
§1 引言
Clifford代數(shù)是復(fù)數(shù),四元數(shù),外代數(shù)的推廣.Clifford分析是關(guān)于Dirac算子零解的函數(shù)理論,Dirac算子是著名的Cauchy-Riemann算子在高維情形下的發(fā)展.Dirac算子特殊的結(jié)構(gòu)使它成為聯(lián)系偏微分方程,微分幾何以及物理學(xué)的重要橋梁,這也使得對Dirac算子的研究具有很重要的意義.1968年,D.Hestenes引入了Dirac算子,并且研究了Dirac算子在Clifford分析中的重要作用,證明了實Clifford分析中的Morera定理及Liouville定理[1].直到1982年,F.Brackx,R.Delanghe,F.Sommen等給出了正則函數(shù)的Cauchy-Riemann方程,Cauchy-Pompeiu公式,Cauchy積分公式,Sokhotski-Plemelj公式,平均值定理,最大模原理,Weierstrass定理等許多結(jié)果[2],從而將單復(fù)分析中全純函數(shù)在高維空間歐氏度量下進行了推廣.隨后,國內(nèi)外許多學(xué)者開始致力于Clifford分析的研究.在國外,K.G¨urlebeck,W.Sprssig,U.K¨ahler,H.Begehr等都對Clifford分析做過大量的研究[3-6].在國內(nèi),杜金元[7],黃沙和喬玉英[8]等較早開始研究Clifford分析,并取得了一系列較好的研究成果.近幾年,喬玉英和王麗萍等又研究了Clifford分析中一些高階奇異積分算子的性質(zhì)及有關(guān)偏微分方程邊值問題,得到了很好的結(jié)果[9-12].然而,為了能更好地描述物體的特征,經(jīng)典Dirac算子已經(jīng)不能滿足要求,譬如各向同性介質(zhì)中的熱傳導(dǎo)問題,可以在經(jīng)典Clifford代數(shù)結(jié)構(gòu)上利用經(jīng)典的Dirac算子進行描述.但對于涉及到非均勻材料的物理問題,譬如各向異性介質(zhì)中的熱傳導(dǎo)問題,經(jīng)典的Dirac算子就不能很好地對這類問題進行描述,就需要在依賴于參數(shù)的Clifford代數(shù)結(jié)構(gòu)上利用加權(quán)Dirac算子進行描述.因此,2012年,A.N.Di.Teodoro,C.J.Vanegas在含參量Clifford代數(shù)下給出了一階meta-monogenic算子的基本解及Cauchy-Pompeiu公式[13].2013 年,C.Balderrama,A.D.Teodoro,A.Infante在含參量Clifford代數(shù)下給出了n階meta-monogenic算子的Cauchy-Pompeiu公式及應(yīng)用[14].2016年,A.G.Eusebio,A.D.Teodoro研究了第一類multi-meta-weighted-monogenic函數(shù)的Cauchy-Pompeiu公式,并給出了非齊次meta-n-weighted-monogenic方程的分布解[15].2017年,A.G.Eusebio,A.D.Teodoro又研究了第二類multi-meta-?-monogenic函數(shù)的積分公式[16].2018年,J.Vanegas,F.Vargas研究了帶有Clifford常數(shù)權(quán)γi ∈An(R)(i=1,2,···,n) 的Dirac算子Dω=的基本解,其中Dω是二階橢圓微分算子的因子,B=(Bij)是對稱的正定矩陣.隨后,J.Vanegas,F.Vargas又給出了該類加權(quán)正則函數(shù)的Borel-Pompeiu公式與Cauchy-積分公式[17].當(dāng)函數(shù)f滿足方程Dωf=0時,則稱其為加權(quán)正則函數(shù).加權(quán)正則函數(shù)是Clifford分析中的一類重要的函數(shù),是正則函數(shù)的推廣,當(dāng)矩陣B是單位矩陣的時候,加權(quán)正則函數(shù)是正則函數(shù).
本文研究加權(quán)正則函數(shù)的一些性質(zhì),文章的結(jié)構(gòu)安排如下:§2回顧了有關(guān)Clifford分析的一些基本知識,加權(quán)Dirac算子的定義以及與加權(quán)Dirac算子有關(guān)的積分公式.§3研究了加權(quán)正則函數(shù)的平均值定理,最大模原理,Weierstrass定理以及一些推論.這些性質(zhì)刻畫了實Clifford分析中加權(quán)正則函數(shù)的基本特征.
§2 預(yù)備知識
設(shè){e1,e2,...,en}是n維歐式空間Rn的一組標準正交基,An(R)是建立在Rn上的2n維實Cli-fford空間,且基底表示為β={eN|N ∈Γn},其中Γn={0,1,2,···,n,12,13,···,123···n},e0為其單位元,An(R)中的基元素可表示為:其中1≤N1<··· 定義a的模為 設(shè)? ?Rn是一個有界域且邊界??充分光滑,接下來考慮定義在?取值于An(R)中的函數(shù)f,則f可表示為其中fN(x)是定義于?上的實值函數(shù).用表示?中r階導(dǎo)數(shù)連續(xù)的函數(shù)的全體, 加權(quán)Dirac算子定義為 便于計算,將Dω表示為 其中ψi=γiei,i=1,2,···,n. 或 當(dāng)ψi=ei時,則(2.4),(2.5)變?yōu)?/p> 其中矩陣B為單位矩陣,加權(quán)Dirac算子Dω退化為經(jīng)典Dirac算子D= 基于正定矩陣的不同分解,例如Cholesky分解B=LLT(L是下三角矩陣,且對角線上元素Lii >0,i=1,2,···,n),平方根分解L′=以及根據(jù)奇異值分解B=UΛUT得到L′′=來構(gòu)造加權(quán)ψi.如果定義ψi是矩陣L的第i行嵌入到了Rn的標準基中,即 經(jīng)計算,滿足 另一個公式也可通過計算得到. 根據(jù)(2.6)所構(gòu)造的加權(quán)ψi是向量值函數(shù),也可以構(gòu)造不是向量值的加權(quán)ψi. 利用引理2.1中的(2),有 之后只考慮(2.8)給定的加權(quán)ψi的形式. 定義2.1設(shè)f ∈若對任意x ∈?,有Dωf=0(fDω=0),則稱f為?上的加權(quán)左(右)正則函數(shù).也簡稱加權(quán)左正則函數(shù)為加權(quán)正則函數(shù). 定義2.2對于Rn內(nèi)任意兩點ξ=(ξ1,ξ2,···,ξn)和x=(x1,x2,···,xn)定義它們之間的非歐氏距離ρ為 其中Aij是矩陣A的元素. 對于Rn內(nèi)任意兩點x,ξ,當(dāng)x/=ξ時,設(shè)它們之間的歐氏距離為r,即r=|x ?ξ|,則有x ?ξ=ry(|y|=1),把此點y和(0,···,0)之間的非歐氏距離記作ρ0,則可以證得ρ0≥c>0. 這是因為y=(y1,···,yn)∈Rn且|y|=1,從而則 又根據(jù)ρ0的定義,顯然?(u1,···,un)還可以表示為下式 從而得到ρ=rρ0.又ρ0≥c,則 其中ωn表示Rn中單位球的表面積. 設(shè)?,??如上所述,對于任意ξ ∈?,以ξ為心,ε為半徑,做n維非歐氏距離超球Uε(ξ)={x ∈?:ρ(x,ξ)<ε},?Uε(ξ)的外法向量取正方向,則曲面?Uε(ξ)的參數(shù)化方程可表示為 其中r(t)是Rn中歐氏距離下單位球的參數(shù)方程,又由于A=B?1,是對稱正定矩陣,顯然 且對上述參數(shù)化方程Jacobian矩陣有如下關(guān)系: 引理2.2(Green積分公式)[17,p7]設(shè)?,??如上所述,u,v:?An是?上的連續(xù)可微函數(shù),則對于加權(quán)Dω算子有如下公式成立 其中dσ=是??在坐標系{ψ1,···,ψn}下An(R)值的面積微元,N=(N1,···,Nn)是??上的外法向量,dμ是??的標量面積微元. 證由 引理2.3(Borel-Pompeiu公式)[17,p11]設(shè)?,??如上所述,u(x) :? ?Rn →An(R),且u(x)在Rn上連續(xù)可微,則有 引理2.4(Cauchy-積分公式)[17,p11]設(shè)?,??如上所述,若u是?內(nèi)的加權(quán)正則函數(shù),則Borel-Pompeiu公式即為Cauchy-積分公式 定理3.1(平均值定理)設(shè)?如上所述,若f是?上的加權(quán)正則函數(shù),則對于任意ξ ∈?,有 證根據(jù)引理2.2和引理2.4,有 又因為f是?上的加權(quán)正則函數(shù),所以對任意x ∈D ??,有Dωf(x)=0,則上式變?yōu)?/p> 又由于矩陣AB=E,E為單位矩陣,則矩陣AB對角線上的元素的和為 從而 代入(3.2),再根據(jù)Green積分公式,有 定理3.2(最大模原理)設(shè)?是Rn中的域,若f是?上的加權(quán)正則函數(shù),如果存在a ∈?,使得 對所有ξ ∈?都成立,則f在?內(nèi)為常函數(shù). 證設(shè)|f(a)|=λ.令?λ={ξ||f(ξ)|=λ},則由于a ∈?λ,則?λ非空.對于任意ξ ∈? ?λ,有|f(ξ)|<λ,又由于|f(ξ)|在?內(nèi)連續(xù),則存在以ξ為心,R′為半徑的n維超球D(ξ,R′)={x ∈?:ρ(x,ξ) 任取ξ ∈?λ,作n維超球D(ξ,R′′)={x ∈?:ρ(x,ξ) 由平均值定理,當(dāng)f ≡1時,有 因此 所以對于任意x ∈D(ξ,R′′),有|f(x)|=λ,即D(ξ,R′′) ??λ,因此?λ在?中是相對開的.又由于?是Rn的非空開的連通子集,所以由球連法,可得在?上對于任意的ξ ∈?,有|f(ξ)|0=λ. 當(dāng)λ=0時,顯然有f(ξ)=0,即f(ξ)在?內(nèi)為常數(shù). 對(3.3)關(guān)于ξi求偏導(dǎo),有 再對(3.3)關(guān)于ξj(j/=i)求偏導(dǎo),有 在(3.4)等式兩邊乘以Bii,再對(3.5)等式兩邊乘以Bij關(guān)于i,j=1,2,···,n分別進行求和,得到 展開即 根據(jù)正定矩陣B的Cholesky分解B=LLT(L是下三角矩陣,且對角線上元素Lii >0,i=1,2,···,n)則將下式 代入(3.6)得 即 從而對所有的N,有 推論3.1設(shè)?如上所述,若f(ξ)在內(nèi)連續(xù),在?內(nèi)是加權(quán)正則函數(shù),則 證如果f(ξ)是常函數(shù),則結(jié)論成立. 假設(shè)f(ξ)是非常函數(shù)的加權(quán)正則函數(shù),由于?是有界域,且f(ξ)在內(nèi)連續(xù),則存在點a ∈使得 如果a ∈??,則 則結(jié)論成立. 假設(shè)a ∈?,則將?分解為?=?1∪?2∪···,其中?j是有界的連通開集,j=1,2,···,則存在j使得a ∈?j,由于對于任意ξ ∈?j,有|f(ξ)| ≤|f(a)|,f(ξ)是加權(quán)正則函數(shù),根據(jù)定理3.2,則f(ξ)在?j內(nèi)為常函數(shù),與已知矛盾,因此 即 推論3.2設(shè)?如上所述,若f(ξ)在?內(nèi)是非常量的加權(quán)正則函數(shù),則對?內(nèi)任意一點ξ,有 定理3.3設(shè)Eω(x,ξ)如上所述,則存在M0,使得 對所有(α1,α2,···,αp)∈{1,2,···,n}p成立. 證利用數(shù)學(xué)歸納法證明. 又由于AB=E,則 從而上式化簡為 且由于 則存在M4>0,使得 假設(shè)j ≤p ?1時成立,即 下證j=p時,成立 事實上 下面首先討論I1.若α1,α2,···,αp?1中存在一數(shù)與αp相同,不妨設(shè)αp?1=αp,則 由假設(shè)存在M6>0,M7>0,使得 則有 即存在M8>0,使得 若α1,α2,...,αp?1任何數(shù)都不等于αp,則有 綜上,由歸納假設(shè)可知,存在M0使得 從而 對所有 都成立. 定理3.4 (Weierstrass定理)假設(shè){fj}(j是正整數(shù))是?中的一列加權(quán)正則函數(shù)列,如果對?中的每個緊集K,任意ε>0,存在自然數(shù)N(ε,K),使得 則存在?上的函數(shù)f,使得 (i)f是?中的加權(quán)正則函數(shù); (ii)對任意多重指標β,函數(shù)列{?βfj}(j是正整數(shù))在?上是內(nèi)閉一致收斂于?βf. 證設(shè)K是?中任意一個緊集,令序列Kj(j=1,2,...)是?的一個正規(guī)窮竭,滿足Kj是緊集,j=1,2,...;則存在i0,使得K ?Ki0. 由加權(quán)正則函數(shù)的Cauchy積分公式,以及fi ?fj是?中的加權(quán)正則函數(shù),從而對所有ξ ∈K和多重指標β有 則當(dāng)i,j ≥N(ε,K)時,有 有界,因而存在M11>0,使得 又由定理3.3可知 則 對于fi,fj的各個元素,i,j=1,2,···,有 這表明?N ∈Γn,序列{fj,N(ξ)}(j=1,2,···,) 是E(?,R)中的Cauchy列,其中E(?,R)是定義在?上取值于R的函數(shù)全體構(gòu)成的集合,則由E(?,R)的完備性可知,存在函數(shù)fN ∈E(?,R),N ∈Γn,使得{?βfi,N(ξ)}在?中內(nèi)閉一致收斂于?βfN(ξ),β為任意多重指標. 再令f=從而{?βfi(ξ)}在?中內(nèi)閉一致收斂于?βf(ξ),當(dāng)β=1,{?fi(ξ)}在?中內(nèi)閉一致收斂于?f(ξ),從而有{Dωfi(ξ)}在?中內(nèi)閉一致收斂于Dωf(ξ).由Dωfi(ξ)=0(i=1,2,···),從而Dωf(ξ)=0,所以f是?中的加權(quán)正則函數(shù).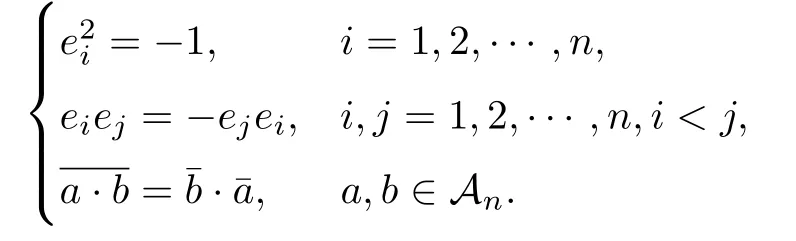
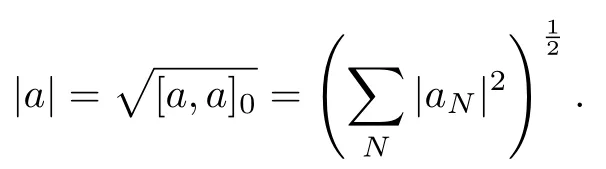
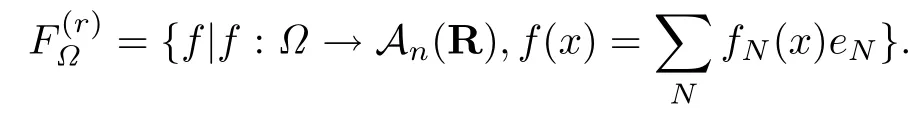
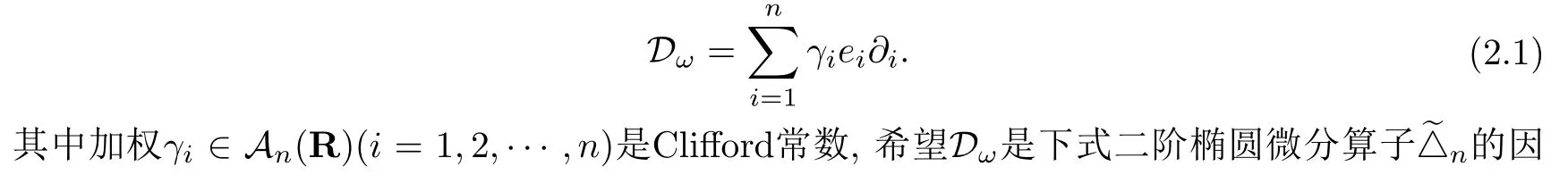


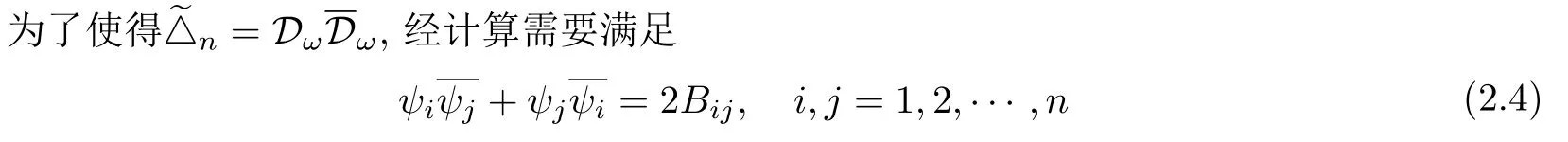
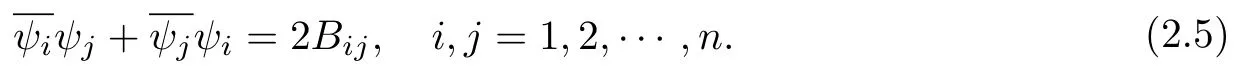
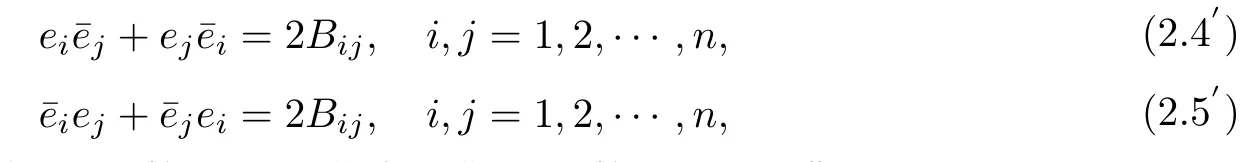

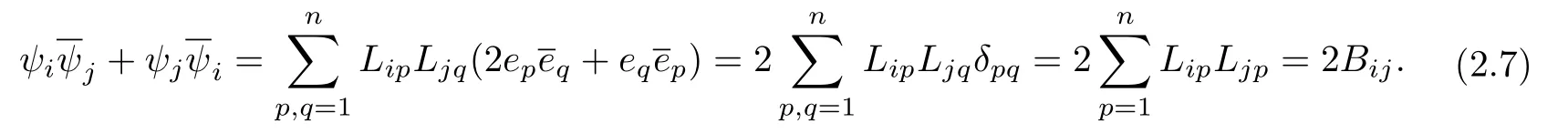

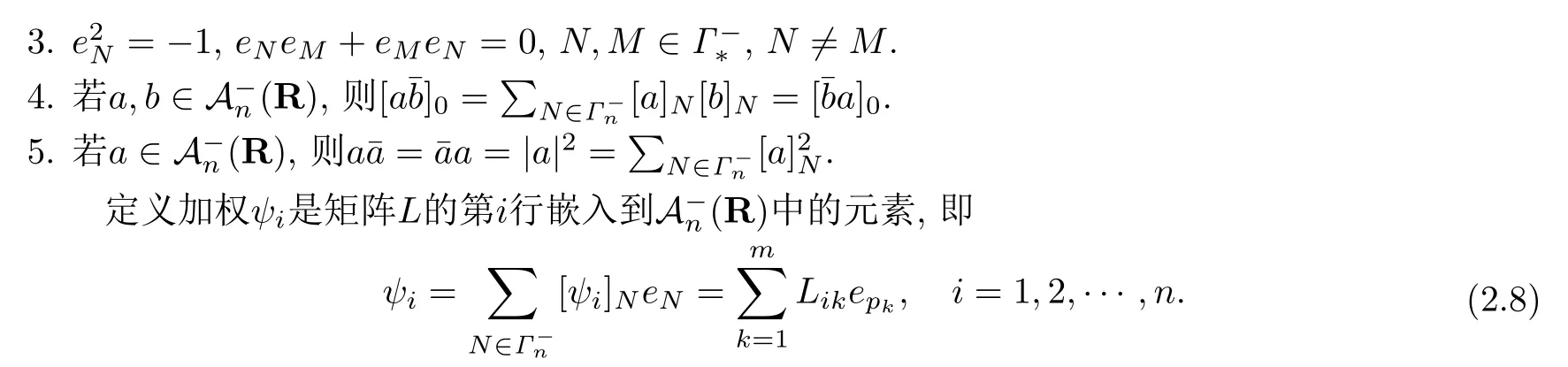
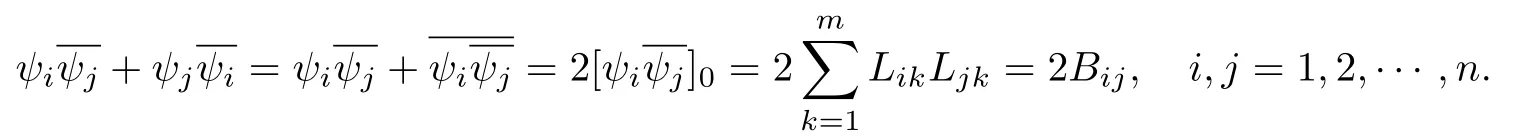
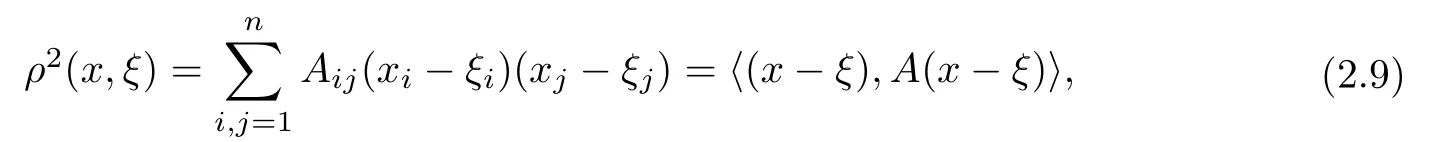
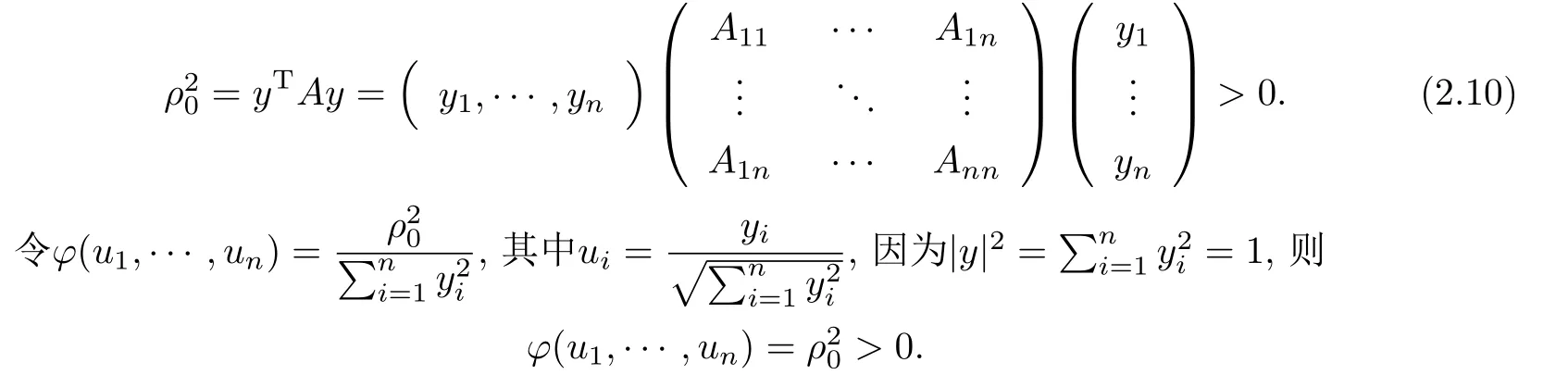
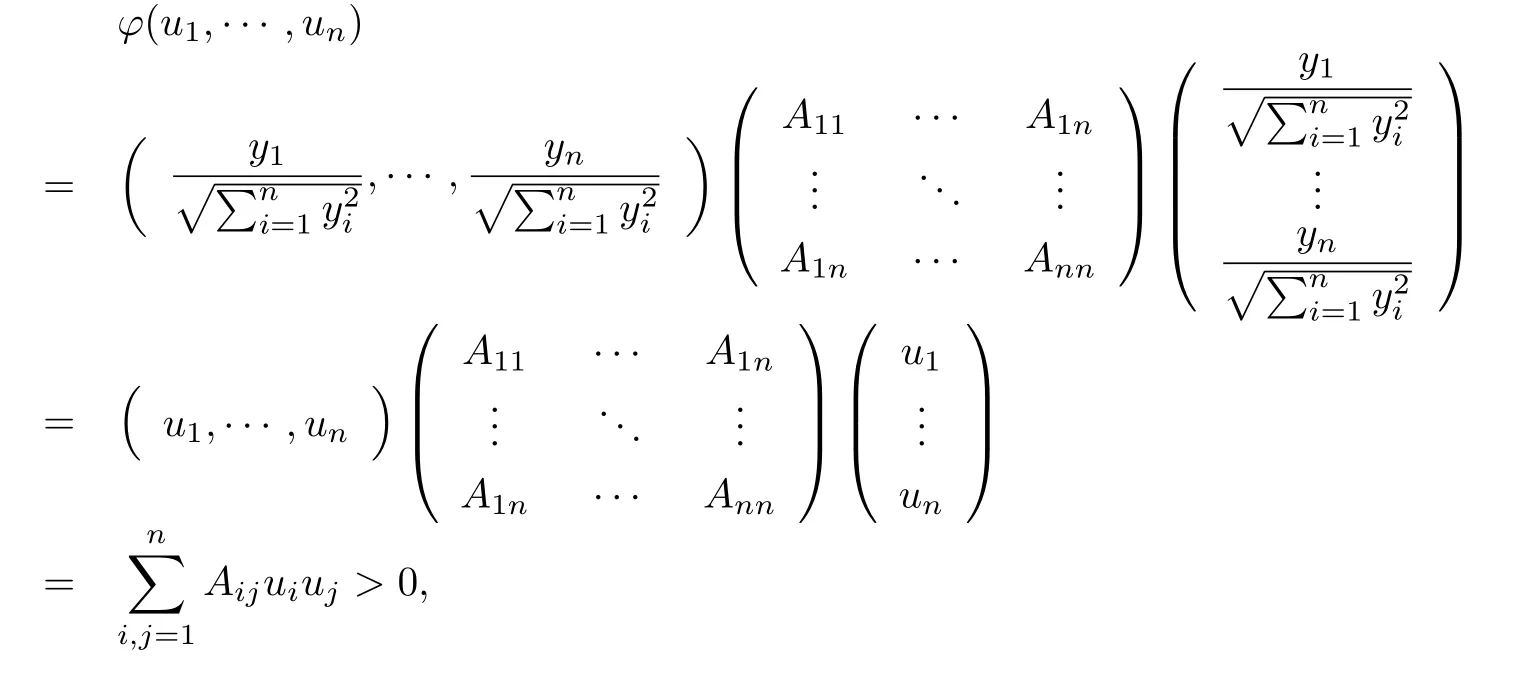


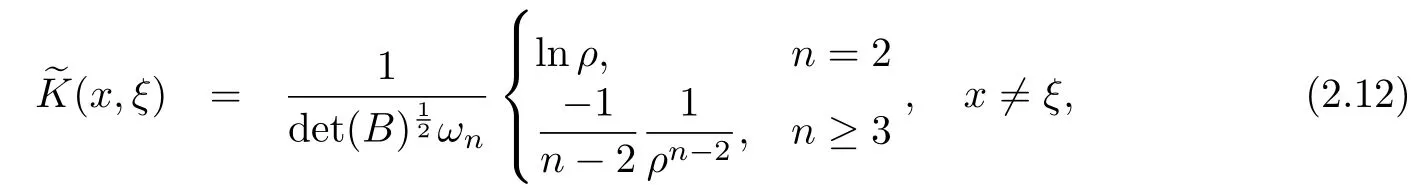
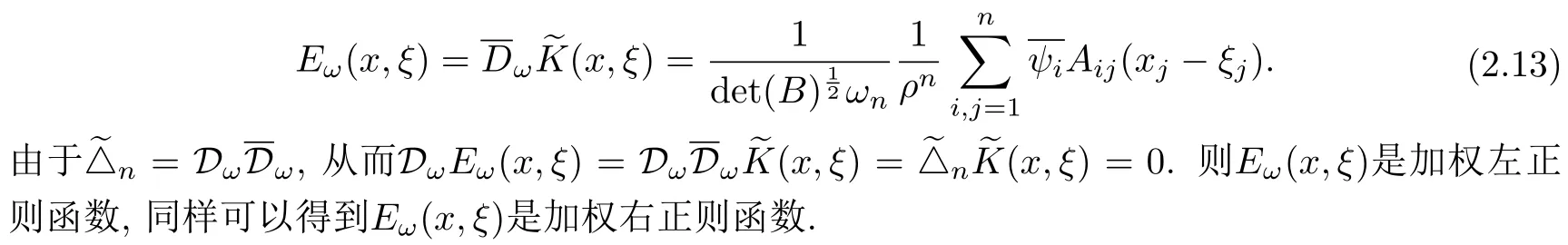
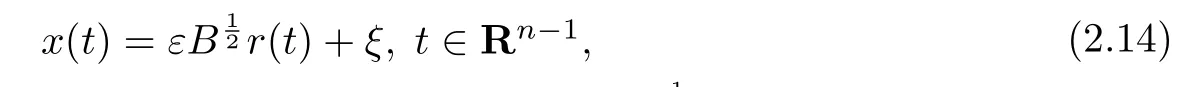
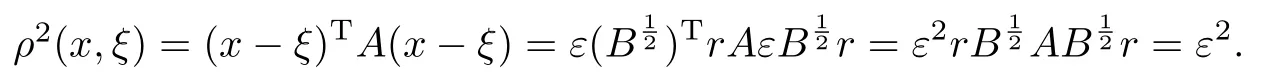
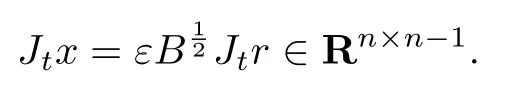
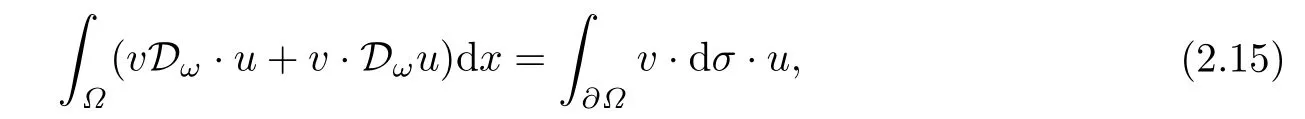
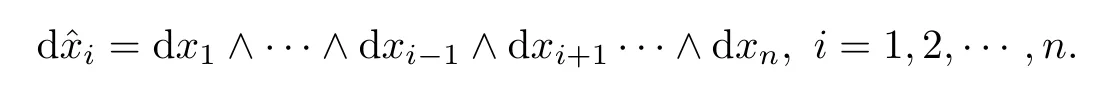
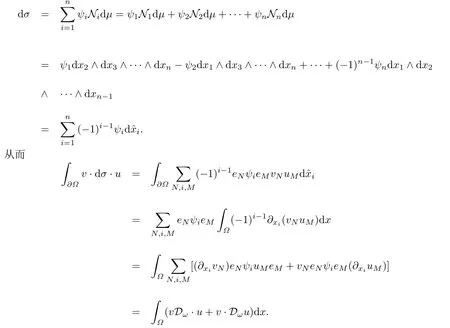
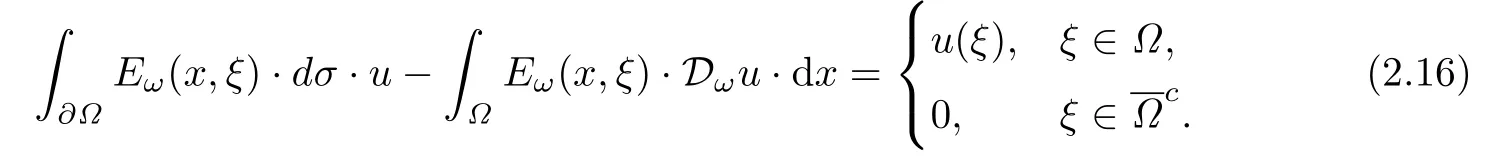
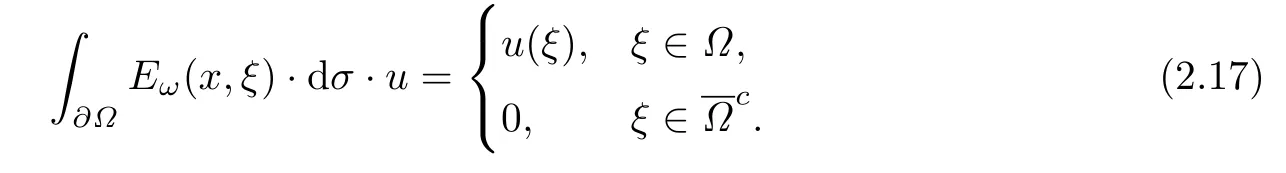
§3 加權(quán)正則函數(shù)的有關(guān)性質(zhì)