王志永, 趙凱

(青島大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,山東 青島 266071)

1.引言

由于歐式空間上的實變量Hardy空間在偏微分方程的研究中起到了至關(guān)重要的作用,所以該空間的相關(guān)理論自上世紀(jì)七十年代以來被大量的研究, 許多重要的結(jié)果被相繼的建立起來.令Δ是Rn上的Laplace算子, 眾所周知, 經(jīng)典的Hardy空間H1(Rn)可以通過極大函數(shù)supt＞0|e-t(-Δ)f(x)|來刻畫.[10]從某種意義上講, 該結(jié)果表明經(jīng)典的Hardy空間H1(Rn)可以看作是與-Δ相關(guān)的Hardy空間.作為經(jīng)典理論的推廣, 自二十世紀(jì)九十年代與微分算子相關(guān)的Hardy空間理論開始得到許多研究者關(guān)注.在Rn空間上,n ≥3, 令L=-Δ+V, 其中位勢V屬于逆Hlder類.1999年, Dziubanski和Zienkiewicz在文[3]中引入了與L相關(guān)的Hardy空間(Rn), 并且借助于局部Hardy空間建立了H1L(Rn)的原子刻畫和Riesz變換刻畫.進(jìn)而借助于Campanato型空間, 在文[4]中, Dziubanski和Zienkiewicz引入了更一般的Hardy型空間Rn),p ＜1.自此之后, 文[3-4]的結(jié)果被推廣到其他二階微分算子, 并且許多與算子相關(guān)的函數(shù)空間被相繼建立起來, 參見文[1,11-12].

令f是Rn上的局部可積函數(shù),B=B(x,r)表示Rn中以x為中心且以r為半徑的球.fB表示f在球B上的平均, 即fB=|B|-1令

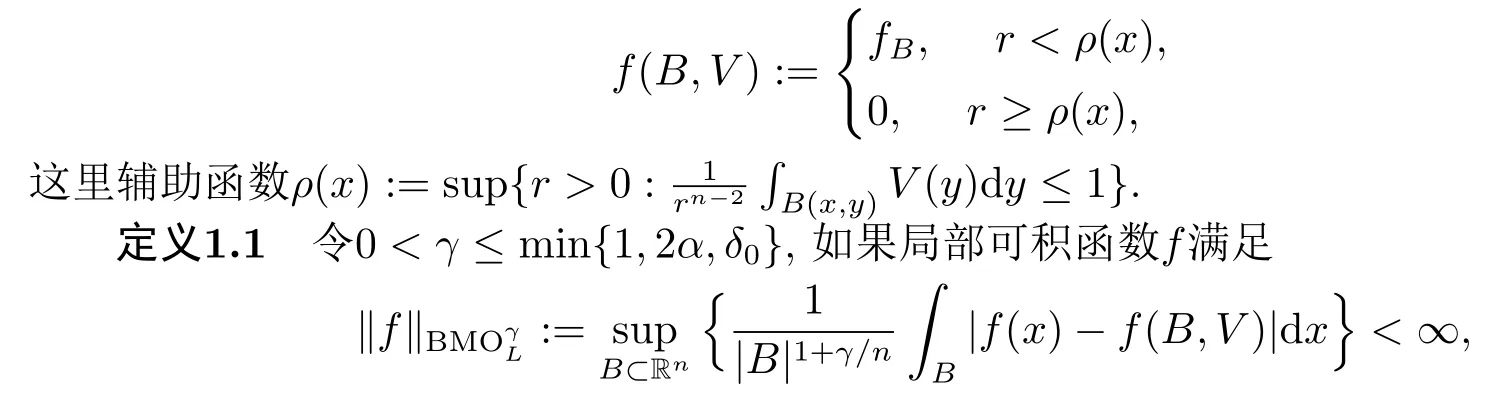
則稱f屬于Campanato型空間(Rn).

引理1.1[9]令0＜γ ≤min{1,2α,δ0},Hardy型空間(Rn)的對偶空間是Campanato型空間(Rn).

與L相關(guān)的極大函數(shù)定義為ML(f)(x):=supt＞0|e-tL(f)(x)|,則Hardy型空間(Rn)的定義如下:

定義1.2對于0＜γ ≤min{1,2α,δ0},Hardy空間(Rn)定義為所有((Rn))*中滿足極大函數(shù)屬于Ln/(n+γ)(Rn)的分布f的全體.其范數(shù)為

眾所周知, 平方函數(shù)刻畫在證明奇異積分算子在Hardy型空間中的有界性中起到了至關(guān)重要的作用.在文[5]中, Fefferman和Stein給出了經(jīng)典Hardy型空間Hp(Rn)的平方函數(shù)刻畫.自此以后, 此類刻畫被推廣到了其他情形, 參見文[3-4,12].定義

利用(1.1), 我們引入與分?jǐn)?shù)階熱半群{e-tLα}t＞0相關(guān)的Lusin面積函數(shù)

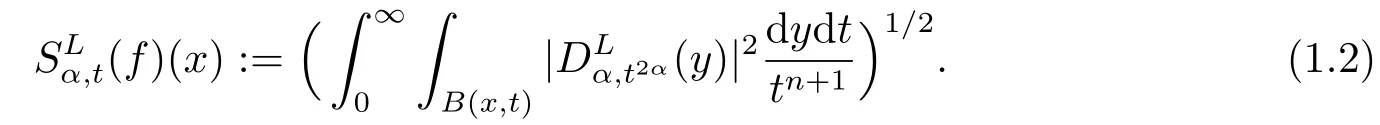
這篇文章的主要目的是借助于由(1.2)定義的平方函數(shù)去刻畫Hardy型空間(Rn).

在本文的剩余部分, 我們用C和c來表示正的常數(shù).這些常數(shù)僅僅與空間的維數(shù), 函數(shù)空間的指標(biāo)以及某些與Schringer算子相關(guān)的參數(shù)有關(guān), 故這些常數(shù)在不同的地方可能取不同的值.所謂B1～B2, 是指存在一個常數(shù)C ＞1, 使得1/C ≤B1/B2≤C.

2.帳篷空間以及基本性質(zhì)

如果存在C ＞0, 使得對任意的球B ?Rn, 逆Hlder不等式

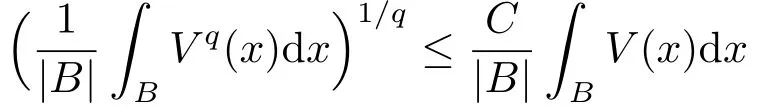
成立, 則非負(fù)位勢V屬于逆Hder類Bq, 1＜q ＜∞.本文中, 我們假設(shè)02.

令δ0=2-n/q,δ=min{1,δ0}并且n/(n+δ)＜p ≤1, 如果函數(shù)a滿足

帳篷空間的原子定義如下:

定義2.2如果函數(shù)α(·,·)滿足

3.分?jǐn)?shù)階熱核的正則性

命題3.1[4](i) 對任意的N ＞0, 存在CN,c ＞0, 使得

接下來, 我們考慮與L相關(guān)的分?jǐn)?shù)階熱半群.對于α ∈(0,1), 用Lα表示算子L的分?jǐn)?shù)次冪,其定義為

通過從屬性公式(3.1)和命題3.1, 在文[8]中, LI等人證明了

命題3.2[8]令0＜α ＜1.

(i) 對任意的N ＞0, 存在常數(shù)CN ＞0, 使得

(ii) 令0＜δ′ ≤min{1,2α,δ0}.對任意的N ＞0, 存在常數(shù)CN ＞0, 使得對任意的|h| ≤t1/2α,

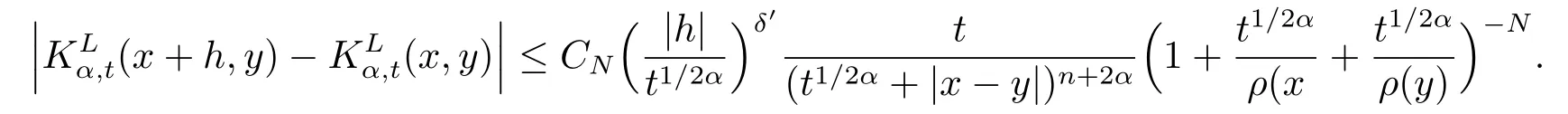
對于t ＞0, 定義

在文[8]中, LI等人給出了核函數(shù)(·,·)的下列估計.

命題3.3[8]令0＜α ＜1.

(i) 對任意的N, 存在常數(shù)CN ＞0, 使得

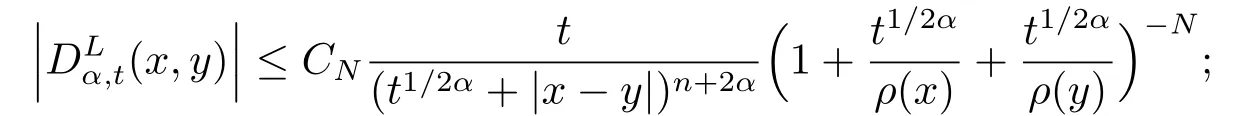
4.Hardy空間的平方函數(shù)刻畫

我們首先給出幾個必要的引理:

所以我們把以下的證明分為兩部分, 首先我們驗證(4.1).利用命題3.3, 可知

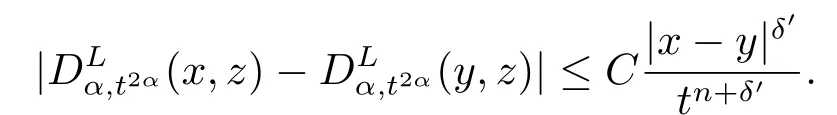
當(dāng)γ=δ′ ≤min{1,2α,δ0}, 可以得到

其次, 我們驗證(4.2), 再次利用命題3.3, 可知

取N=γ, 有

對于x ∈Bc(x0,2r)和y ∈B(x0,r), 則|x-y|～|x-x0|.考慮以下兩種情況:

情形1α ∈(1/2,1).在這種情形下, 令l=n+1, 得到

最后我們有

這就完成了本定理的證明.