Error Analysis of Kernel Regularized Regression with Deterministic Spherical Scattered Data
LI Junyi(李峻屹), SHENG Baohuai(盛寶懷)
(1.Department of Information Technology, Shanxi Police College, Xi’an 710021, China;2.Department of Applied Statistics, Shaoxing University, Shaoxing 312000, China)
Abstract: We investigate the error bounds of kernel regularized regression learning associated with deterministic data on the spherical cap (and the whole unit sphere) and the quadratic loss.We transform the learning error as the upper bound estimate for the numerical integration error and obtain the learning rates with the convergence rates of kernel-based quadrature.We express the learning rates with a modulus of smoothness which is equivalent to a K-functional in learning theory.The research results show that the learning rates are controlled by the mesh norm of the scattered data.
Key words: Number integration formula; Spherical cap; Worst-case error; Quadratic function loss; Kernel regularized regression; Learning rate
1.Introduction
It is known that learning theory is a new field of application and computation mathematics,many contributions have been done.[1?3]Among these researches,learning associating with spherical harmonics has been getting a lot of attentions.[4?5]Since kernel regularized approach associated with deterministic scattered data has found valuable applications in various fields of numerical analysis, including interpolation, meshless methods for solving partial differential equation, neural networks, machine learning, identification, recognition and control[6?9]and the kernel regularized framework has been established[10?11], it is necessary for us to give investigation on the performance of kernel regularized learning associating with determined spherical data.This paper provides a new method of deriving deterministic error bounds for the kernel regularized regression associated with kernel functionals on the unit sphere.We show how the error estimates of kernel-based quadrature in the deterministic setting associated with the reproducing kernel Hilbert space(RKHS)on the unit sphere are used to bound the learning rates and show that the learning rates are determined by the mesh norm of the scattered data.

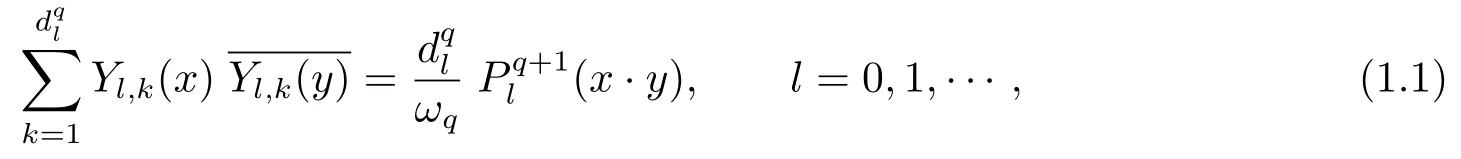
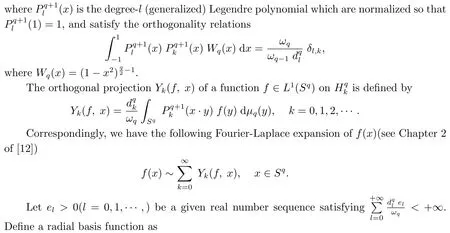

Then,by Theorem 17.8 in[9],we know for given pairwise distinct pointsXN:={ξ1,ξ2,··· ,ξN}?Sq, the matrixAN:= (K(ξi, ξj))N×Nis positive definite.Therefore,K(x,y) is a Mercer kernel onSq×Sqwithelbeing its eigenvalues.
Define a nature spaceNφas

with the inner product
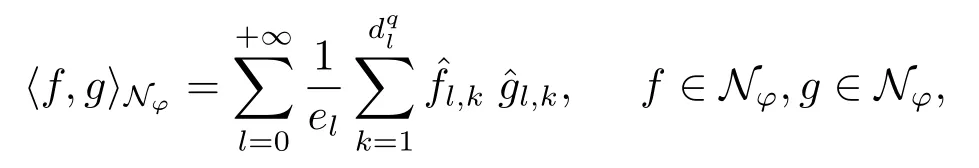

Define aK-functional

and a general modulus of smoothness as
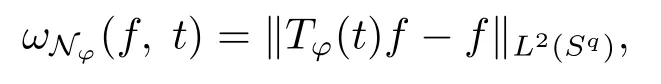
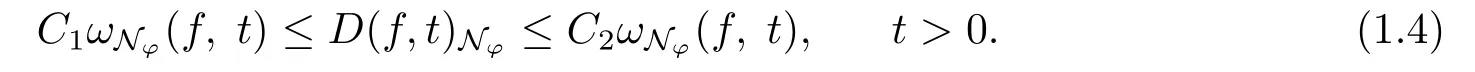
Letz ∈Sqbe a given point,B(z;γ) ={x ∈Sq:x·z ≥cosγ}={x ∈Sq:d(x,z) =arccos(x·z)≤γ}be the spherical cap with centerz ∈Sqand radiusγ ∈(0,π).Herex·zdenotes the Euclidean inner product ofxandzin Rq+1.
We shall bound the learning rate of the kernel regularized regression on scattered data on the spherical capB(z;γ)and the whole unit sphereSqin Section 2 and Section 3 respectively.The discussions are along the following lines.We first provide the worst-case error bounds for kernel-based quadrature for kernel (1.2) with(see Proposition 2.1 and Proposition 3.1).Basing on these results, we establish the kernel regularized learning frameworks associated with scattered data onB(z;γ) andSqrespectively and then give the learning rates with the equivalent relation (1.4) and the worst-case error bounds.
2.Learning Rates on a Spherical Cap
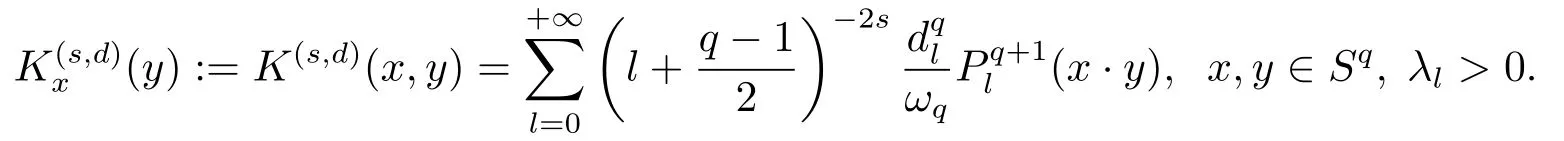
Define the Sobolev spaceHK(s,q)=Hs,qas
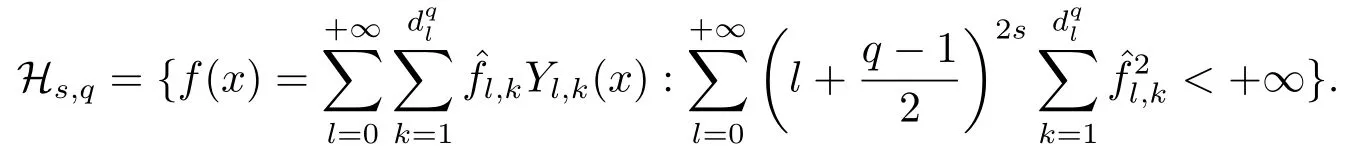
ThenHs,qis a RKHS with an inner product defined as

i.e.,
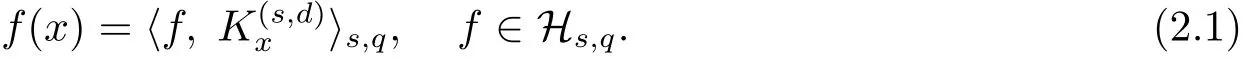
Moreover, there holds (see (2.8) of [14])
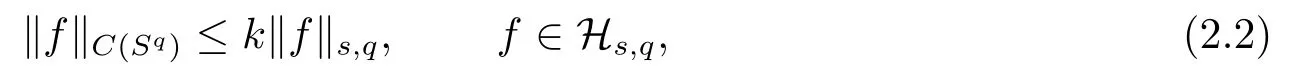
Considerm-point rulesfor numerical integration over the spherical capB(z;γ),

with nodesxj ∈B(z;γ) and weightswj ∈R,j=1,2,··· ,m,for approximating the integral

of a continuous functionf,defined onSq,over the spherical capB(z;γ).The worst-case errorE() ofin Hilbert spaceHs,qis defined by
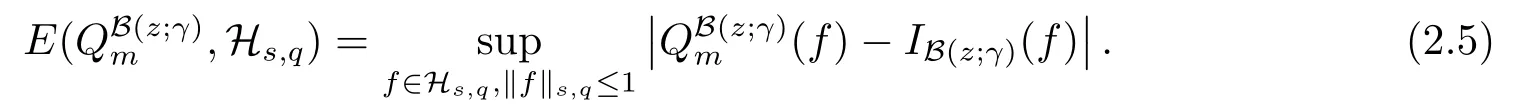

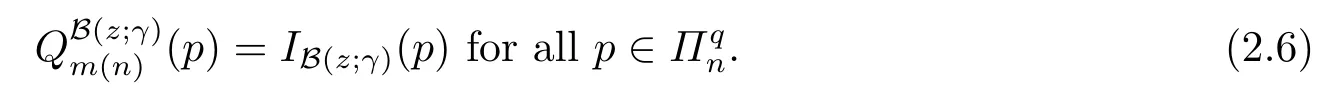
The worst-case error ofinHs,qsatisfies the estimate
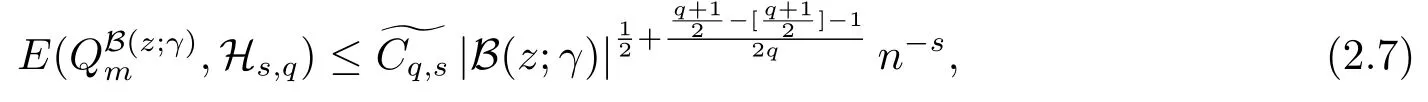
where[a] denote the biggest integer≤a,|B(z;γ)|is the area of the spherical capB(z;γ), and
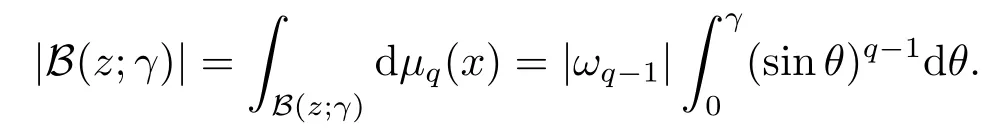
It follows


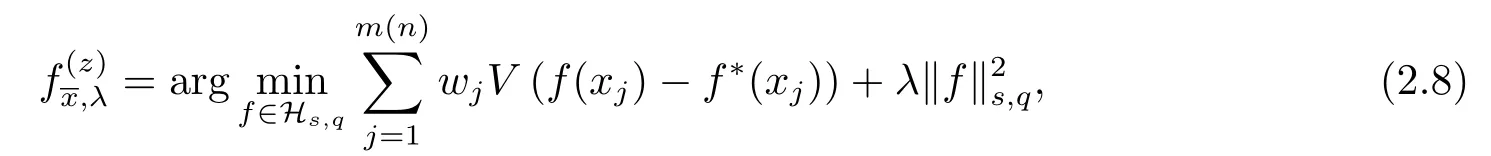
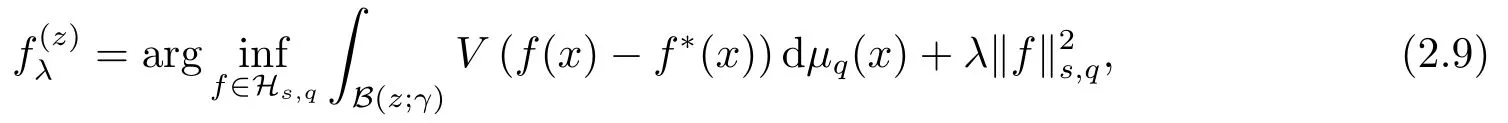
Theorem 2.1Letbe the solution of (2.8) andf?∈L2(Sq).Then there exists a constantC=C(s,q,k)>0 such that
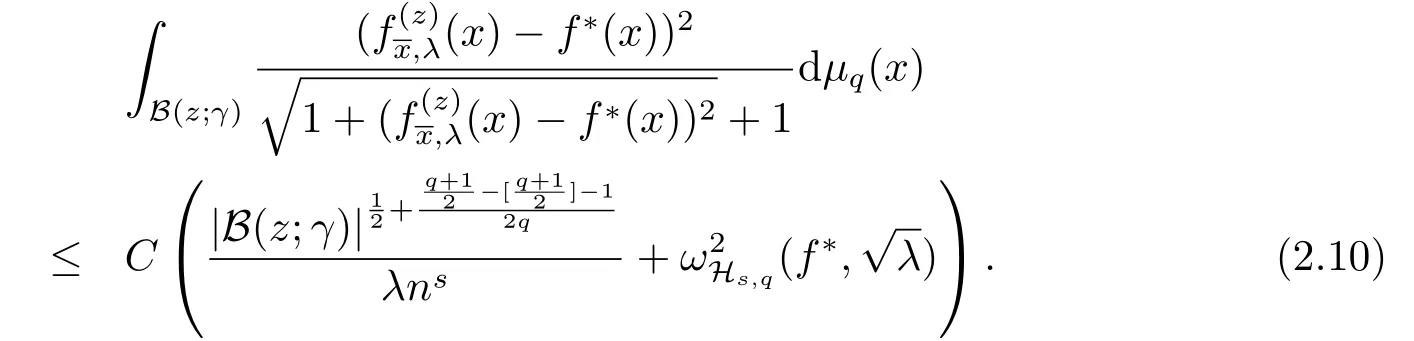
To show Theorem 2.1, we first give a lemma.
Lemma 2.1Letandbe defined as in (2.8) and (2.9) respectively.Then

Proof(2.11) can be obtained from (1.7) of [16] by takingy=f?(x) andV(t) =?1 or it can be obtained from (5.14) in Chapter 5 of [3].
Proof of Theorem 2.1Simple computations yields

where

By the mean value theorem we have



where
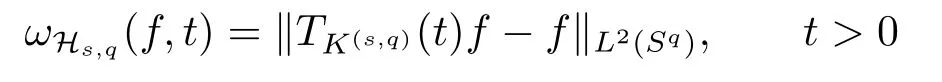
and
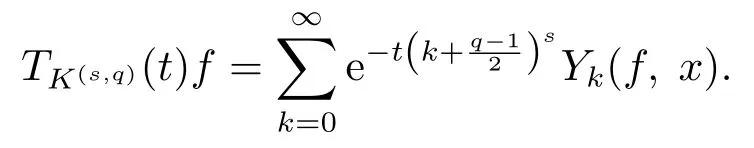

It follows by (2.7), (2.16) and (2.11) that
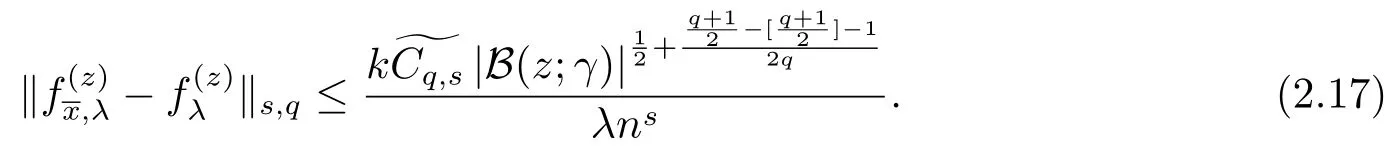
(2.17),(2.14)together with(2.12)give(2.10).Since=0, takingλ=n?θ,0<θ Corollary 2.1Letbe the solution of (2.8) andf?∈L2(Sq).Then there holds almost everywhere the following convergence Proof(2.19) can be obtained by (2.10) and the fact thatV(t)=?1→0+?|t|→0+. Considerm-point rulesQmfor numerical integration over the whole unit sphereSq, with nodesxj ∈Sqand weightswj ∈R,j=1,2,··· ,m,for approximating the integral of a continuous functionf, defined onSq.The worst-case errorE(Qm,Hs,q)ofQmin Hilbert spaceHs,qis defined by Proposition 3.1[14]Forq ≥2 andthere exists a positive constantcsuch that for any positive weightm(n)-point numerical integration ruleQm(n), withQm(n)(p) =pfor all The constantcdepends only onsandq. We give a lemma to show that the conditions in Proposition 3.1 is satisfied. Define the mesh normnd the separation diameterfor a data?Sqby Theorem 3.1Letbe the solution of (3.7) andf?∈L2(Sq).Then there exists a constantC=C(s,q,k)>0 such that Proof(3.8) can be obtained by replacingB(z;γ) in (2.11) and (2.18) withSq. Since the worst-case bounds (2.7) and (3.4) are determined by the mesh norm of the scattered datawe can say that the learning rates of the algorithms (2.8) and (3.7) are controlled by the mesh norm as well.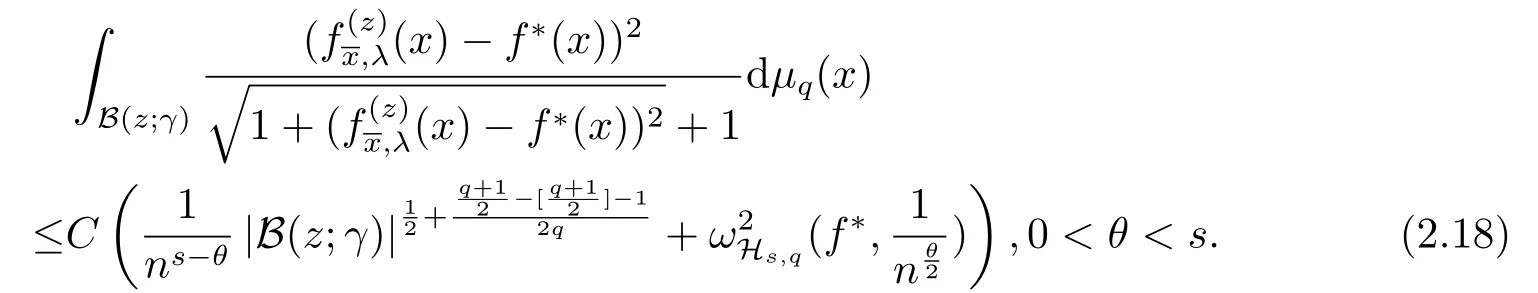
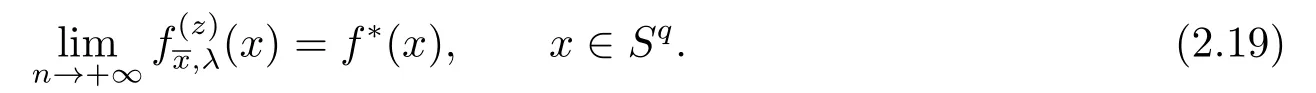
3.Learning Rates on the Whole Unit Sphere




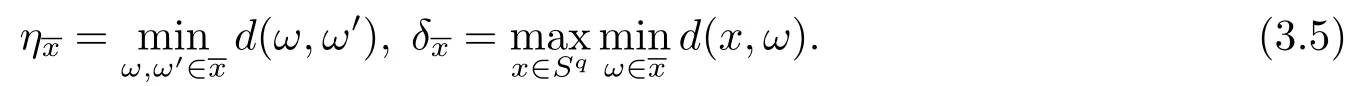
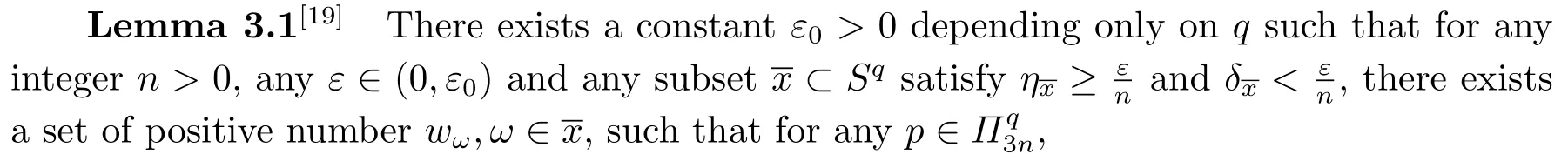
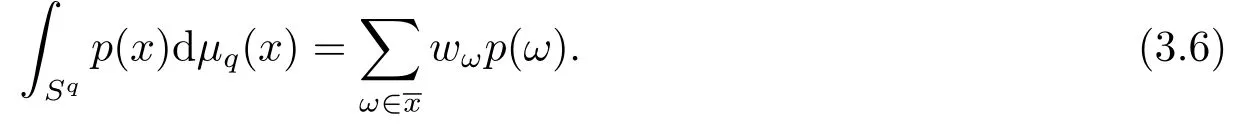

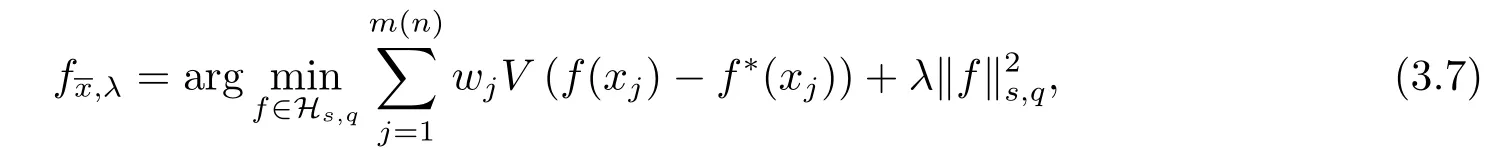
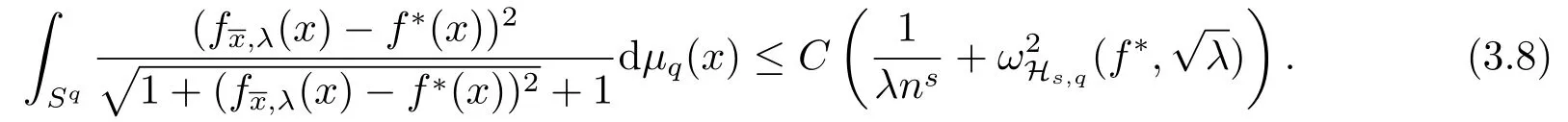
- 應用數(shù)學的其它文章
- 基于不確定控制理論的最優(yōu)策略研究
- Dependence of Eigenvalues of Two-Interval Third-Order Boundary Value Problems
- 一類擬線性薛定諤方程非平凡解的存在性
- The Optimal Error Estimates for the Dynamic Magnetic Field of Solar Interface Problem by H(curl,Ω) Finite Element Methods
- 協(xié)變量維數(shù)可以趨于無窮的縱向數(shù)據(jù)的廣義估計方程分析
- 不可壓磁流體力學方程組的高精度數(shù)值解法

