CHEN Yu(陳玉), KUANG Kai(鄺凱), YAN Xueling(顏學(xué)鈴)

(School of Mathematics and Statistics, Guangxi Normal University, Guilin 541004, China)

Abstract: In this paper, we propose a new converse duality theorem of higher order Wolfe type duality for multiobjetive programming with cone constraints under appropriate assumptions.This overcomes some drawbacks in the results of Kim et al.(2010).

Key words: Multiobjective programming; Higher order Wolfe duality; Cone; Converse duality theorem

1.Introduction

Consider the multiobjective programming problem

whereφ=(φ1,φ2,··· ,φl(shuí)),g=(g1,g2,··· ,gm)and each component functionφi,gi:Rn →R are twice continuously differentiable.C ?Rndenotes a closed convex cone with nonempty interiors andC?is the polar cone ofC.

It is well known that duality has significant impact on the solutions of nonlinear programming.Compared with first order duality, higher order duality can obtain better properties about bounds for the objective function value of the primal problem[1], therefore it has been attracted by many researchers,such as Agarwal,Ahmad and Jayswal[2],CHEN[3],Gupta and Jayswal[4], Kim, Kang and Lee[5], YANG[6?10], GAO[11], Khushboo, Jai and Izhar[12]and so on.Among them, Kim[5]established the higher order Wolfe type and Mond-Weir type dual models involving cone constraints.Furthermore, under the condition of higher order generalized invexity, weak duality theorem, strong duality theorem and converse duality theorem were presented, respectively.For higher order Mond-Weir type multiobjective programming,YANG[8]gave a converse duality theorem under mild assumptions by correcting some error in the results of[5].At the same time,for higher order Wolfe type dual model,YANG[8]pointed out that there is a flaw for the Wolfe type converse duality theorem in [5], and it still has not been corrected.

In this paper,a new higher order converse duality theorem is investigated for higher order Wolfe type multiobjetive programming with cone constraints under appropriate assumptions.This fills some gaps in the results of [5].

2.Preliminaries

Firstly, we give some notations and definitions which are used in this paper.

Rndenotes then-dimensional Euclidean space, and Rn+is its nonnegative orthant.For anyy,z ∈Rn, we use the following ordering relations:y < z ?z ?y ∈int,y ≤z ?z ?y ∈{0},y ?z ?z ?y ∈

Definition 2.1[5]A nonempty setS ?Rnis said to be a cone if for anyz ∈Sandλ ∈[0,+∞), one have thatλz ∈S.

Moreover, the coneSis called a convex cone ifSis convex.

DefineS?={w ∈Rm:zTw ≤0,?z ∈S}, andS?is said to the polar cone ofS.

Definition 2.2[4]A pointz?∈Sis said to be an efficient solution of (MCP), if there exists no otherz ∈Ssuch thatφ(z)?φ(z?)∈S{0}.

Definition 2.3[5]LetS ?Rnbe open andh:S×Rn →R be a differentiable function.A differentiable functionφ:S →R is said to be higher order invex, if there exists a functionη:S×S →Rnsuch that

φ(z)?φ(u)≥η(z,u)T?ph(u,p)+h(u,p)?pT?ph(u,p),for allz,u ∈S.

Definition 2.4[13]A functionF:Rn×Rn×Rn →R is said to be sublinear, if for all(z,u)∈Rn×Rn,a1,a2∈Rn, α ∈R+anda ∈Rn, the following conditions are satisfied,

(i)F(z,u,a1+a2)≤F(z,u,a1)+F(z,u,a2),

(ii)F(z,u,αa)=αF(z,u,a) .

Definition 2.5[13]LetFbe a sublinear function andd(.,.) be a metric on Rn,ρ=(ρ1,...,ρk)∈Rk.The functionφis said to be (F,ρ)-convex atu, if for allz ∈S, it holds that

φ(z)?φ(u)≥F(z,u;?φ(u))+ρd(z,u).

According toρ >0, ρ= 0 orρ <0, we say that this functionφis stronglyF-convex,F-convex or weaklyF-convex atu, respectively.

We now give the higher order Wolfe type dual for multiobjective programming involving cone constraints in[5]as follows.However,since the first constraint implies that the last term of the objective function should not exist in their higher order Wolfe type dual, the following dual is slightly different from the one in [5].

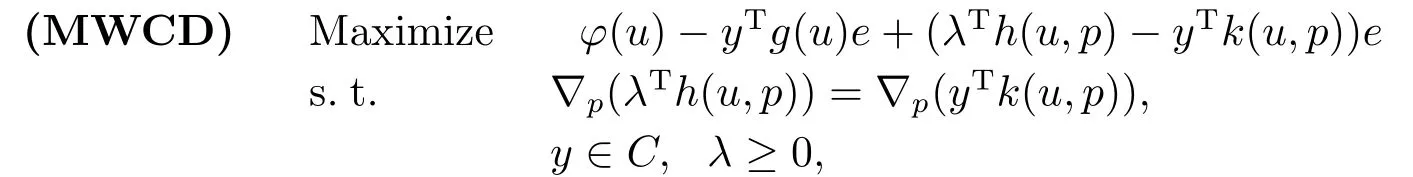
wherekdenote the differentiable function from Rn×Rn →Rm.The vectore=(1,1,1,··· ,1)T∈Rlis the all-ones vector and the vectorλ ∈Rl.

For the above Wolfe dual model, Kim[5]established the weak duality theorem, i.e., Theorem 3.1 in [5].We also make the corresponding revisions.In particular, the conclusion of this theorem has been slightly modified.However, its proof is parallel to one in [5].

Lemma 2.1Letzbe a feasible solution of (MCP) and (u,y,λ,p) be a feasible solution for (MWCD) andλ>0(λTe=1).Suppose thatFis a sublinear function and the following conditions are satisfied,

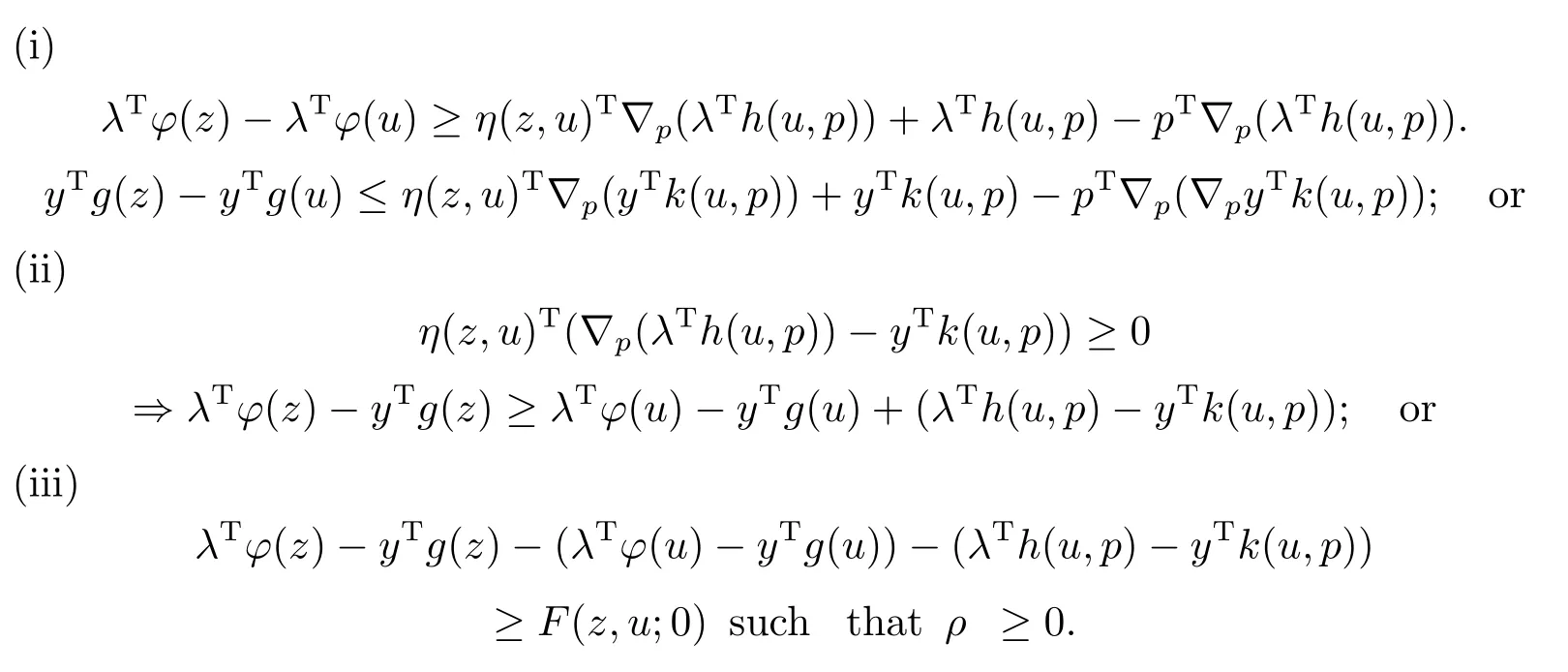
Then

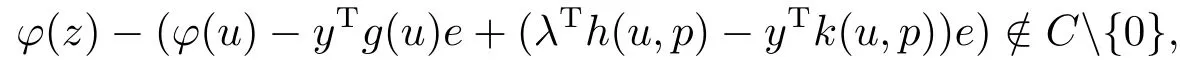
whereCis a closed convex pointed cone with nonempty interiors in Rlandη:C×C →Rn.

The converse duality theorem is also obtained by Kim et al.for the Wolfe higher order multiobjective dual models, i.e., Theorem 3.3 in [5].

Lemma 2.2[5]Let(z?,y?,λ?,p?)be an efficient solution of(MWCD)and the conditions of Theorem 2.1 hold.Suppose that the following conditions are satisfied,

(i)h(z?,0)=0, k(z?,0)=0, ?ph(z?,0)=?φ(z?), ?pk(z?,0)=?g(z?);

(ii)?p[?((λ?)Tφ(z?))+?((λ?)Th(z?,p?))??((y?)Tg(z?))??((y?)Tk(z?,p?))]is negative or positive definite;

(iii)=1,2,···,land=1,2,···,mare linearly independent.Thenz?is an efficient solution of (MCP).

Remark 2.1As pointed out by YANG[8], the converse duality theorem of Wolfe dual model (see Theorem 3.3 in [5]) didn’t hold.In their proof of the above theorem,they have differentiated the equalityβT[?(λ?)Tφ(z?) +?(λ?)Th(z?,p?)??(y?)Tg(z?)??(y?)Tk(z?,p?)] = 0 with respect topto yieldβT?p[?(λ?)Tφ(z?) +?(λ?)Th(z?,p?)??(y?)Tg(z?)??(y?)Tk(z?,p?)]=0.Obviously there exists a flaw.

3.Higher Order Wolfe Converse Duality Theorem

In this section, in order to guarantee that the converse duality theorem holds for the Wolfe higher order multiobjective dual models, we replace the condition (ii) of Lemma 2.2 by the following two conditions, i.e., the conditions (ii) and (iii) of Theorem 3.1.The modified converse duality theorem, which rectifies Lemma 2.2, is presented as follows.

Theorem 3.1Let(z?,y?,λ?,p?)be an efficient solution of(MWCD)and the conditions of Lemma 2.1 hold.Suppose that the following conditions hold,

(i)h(z?,0)=0, k(z?,0)=0;

(ii){?φi(z?),i= 1,2,··· ,l}are linearly independent, where?φi(z?) denotes thei-th column of?φ(z?);

(iii)?z((y?)Tg(z?))?(?z((λ?)Th(z?,p?))??z((y?)Tk(z?,p?)))0?p?=0;

(iv)the vectors{[(λ?)Th(z?,p?)(y?)Tk(z?,p?)]j, j= 1,2··· ,n}are linearly independent.

Thenz?is an efficient solution to (MCP).

ProofIn view of the generalized Fritz John theorem in [14], since (z?,y?,λ?,p?) is an efficient solution to (MWCD), there existα ∈Rl,β ∈Rn,γ ∈C?andδ ∈Rlsuch that

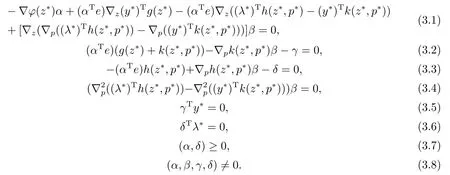
In view of (iv)and (3.4), one gets

The first objective is to prove that0.Ifα=0, taking into account (3.2) and (3.3),we haveγ=0 andδ=0.This contradicts (3.8).Thereforeα0, i.e.,αTe>0.Combining(3.9) with (3.1), we immediately obtain the inclusion

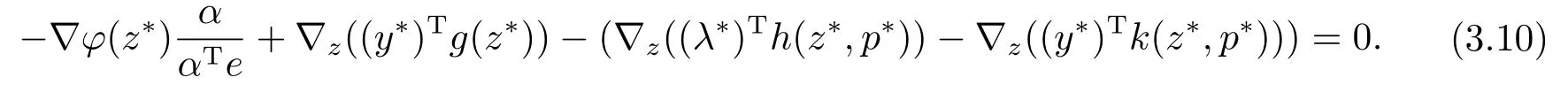
Noting (ii),α ≥0 andαTe>0, we have shown that

This together with (3.10) implies that

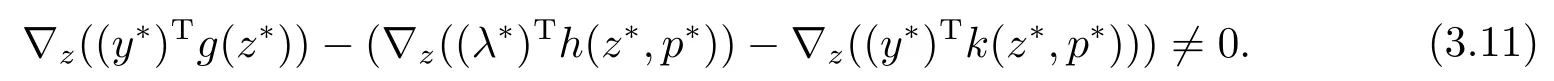
From (iii) and (3.11), it follows that

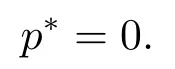
Multiplying (3.2) by (y?)Tand using (3.5) and (3.9), we obtain

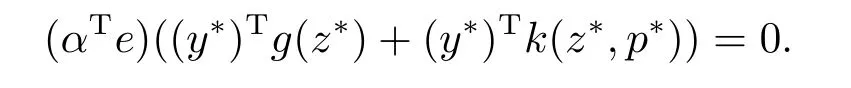
UsingαTe>0,p?=0,we see that

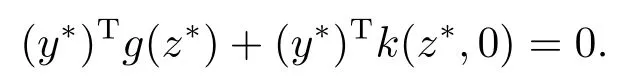
From (i), one gets

This implies that (y?)Tg(z?)≥0.Sincey?∈C, then?g(z?)∈C?.This implies thatz?is feasible for (MCP).In view of thatp?= 0 and (i), we obtain the equal value for (MCP)and(MWCD),i.e.,φ(z?)=φ(z?)?(y?)Tg(z?)e+(λTh(z?,0)?(y?)Tk(z?,0))e.Suppose thatz?is not an efficient solution of (MCP), then, from the definition of an efficient solution for(MCP), there existsz ∈{z:?g(z)∈C?}such thatφ(z)?φ(z?)∈C{0}, i.e.,φ(z)?(φ(z?)?(y?)Tg(z?)e+(λTh(z?,0)?(y?)Tk(z?,0))e)∈C{0}, which yields to a contradiction with the conclusion of Lemma 2.1.The proof is completed.