Adaptive synchronization of chaotic systems with less measurement and actuation?
Shun-Jie Li(李順杰) Ya-Wen Wu(吳雅文) and Gang Zheng(鄭剛)
1School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing 201144,China
2INRIA Lille-Nord Europe,40 Avenue Halley,59650,Villeneuve d’Ascq,France
Keywords: chaotic systems,adaptive synchronization,linear matrix inequality
1. Introduction
Since it was introduced by Pecora and Carroll[1]in 1990, the synchronization of chaotic systems has attracted increasing attention due to its possible applications in secure communication,[2–5]biomedical engineering,[6]information science,[7–9]and chemical reactions,[10,11]etc. A wide variety of control methods of chaos synchronization have been studied, such as observer design with or without time delay,[5,12,13]linear feedback control method,[14–16]sliding mode control,[17,18]adaptive control method,[19–27]and backstepping control method.[28–30]
In 2005, Huang[22]showed that if the vector function of a chaotic system is Lipschitz, then the synchronization problem can be achieved by an adaptive control scheme while the controllers are implemented to all the state variables. However,it has been revealed in the literature that not all the states are necessary to be controlled in order to achieve synchronization. For example,Liaoet al.[19]showed that synchronization of a Lorenz system can be achieved only by a single adaptive feedback controller that is acted on the first or the second state equation.Similar results can be found for the Chen system,[20]the Rikitake system and the hyperchaotic R¨ossler system,[23]etc. Guo[23]proposed a method to reduce the number of controlled states and also observed that selecting only a part of states to be controlled does not always lead to synchronization.Thus an interesting question arises: how to verify whether the synchronization between two identical chaotic systems can be achieved if certain number of state variables are chosen to be controlled, and how to choose those state variables? To the best of our knowledge,there does not exist such a result in the literature.
Motivated by the aforementioned analysis,we investigate the above question in this article. A sufficient condition is derived based on the Lyapunov stability theory and it generalizes the results in Ref.[22],and also in Ref.[23](in a similar way).In most cases,this condition can be formulated as an LMI feasibility problem which can be efficiently solved by numerical tool,such as LMI solver of Matlab.
The rest of this article is organized as follows. Section 2 presents the main result and its proof. Section 3 gives the applications of the proposed results to the adaptive synchronization for the Rikitake system and the hyperchaotic Liu system.Numerical simulations are given in Section 4. Finally, Section 5 contains the conclusion.
2. Sufficient conditions for identical chaotic synchronization
Consider the following nonlinear system

Assumption 1 For anyx=(x1,...,xn)T∈Ωand ?x=(?x1,...,?xn)T∈Ω, there exists a positive semi-definite matrixMsuch that


For a given nonlinear system of the form(1), let us construct the following nonlinear dynamics to achieve the synchronization objective

wherez=(z1,...,zn)Tis the state,u=(u1,...,um)Tdenotes the designed control,andB ∈Rn×m,named as the‘a(chǎn)ctive matrix’beforeu,is to determine the controller for which lines of system(3)will be activated. For simplicity,when thei-th row ofBis not zero, then we can say that the relative controller will be activated for thei-th row.
It is evident that the synchronization between systems(1)and (3) can be easily achieved if we have all statesxof system (1) (i.e.,C=In×n, which means that all statesxcan be measured for system(1),and can be used to design controlleruin system (3)) and if we active relative controllers for each line in system(3)(i.e.,B=In×n,which means each line has an independent controllerui). However, an interesting question,as stated in the introduction,is: Can we use less measurement of system(1)to active fewer controllersuin system(3)? The positive answer of this question will be more applausive since fewer sensors are needed for system (1) to measure only the necessary states,and less energy will be consumed to actuate some necessaryuin system(3).
To answer the above question,let us note
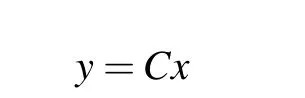
as the necessary states for the purpose of achieving synchronization between systems (1) and (3). In practice, those necessary states are respectively measured by different sensors.Thus,without loss of generality,we can assume thatC ∈Rm×nis of full row rank. Moreover,it is assumed that each row ofCcontains only one non-zero element which provides the measurement of one necessary state. We would like to emphasize that such an assumption is not restrictive at all,since ifCis not of such a form,then there will exist two invertible matricesQ1andQ2such thatCcan be transformed intoQ1CQ2,which is exactly of the assumed form.
In order to achieve the synchronization between systems(1)and(3),we investigate the following output feedback control law:


whereL=diag{l1,...,ln}. Obviously,inequality(11)can be always true ifLis sufficient large,which implies that the result in Ref.[22]is just a special case of Theorem 1.
Remark 5 In a similar way, we can also obtain an extended version of the result in Ref.[23]wherek1=···=km=k ∈R, which is updated by the adaptive law ˙k=?γΣmj=1e2τjwithγ>0 being an arbitrary positive constant.
3. Applications
In this section,two examples are presented in order to verify the effectiveness and correctness of the proposed methodologies.
Example 1 The Rikitake system.[23,34]
The dynamics of the Rikitake system is of the form (1)with

wherea=5,μ=2. The state trajectoriesx1(t),x2(t),x3(t)are globally bounded and hence,there exist three positive real constantsDi,1≤i ≤3, such that|xi(t)|≤Di,1≤i ≤3 hold for allt ≥0.

wherea= 10,b= 35,c= 1.4,d= 5. The state trajectoriesx1(t),x2(t),x3(t),x4(t)are globally bounded and hence,

4. Numerical simulations
In this section, numerical simulations by MATLAB will be given and the fourth-order Runge–Kutta method is applied to approximate the solution of differential equations with a small chosen fixed time step size.
For the Rikitake system,the initial conditions of the master system and the salve system are chosen asx(0)=(2,?1,4)andz(0)=(?3,1,6),respectively. Selectγ=5 and the initial conditions of the feedback gain byk(0)=1. Figure 1 shows that the error states are asymptotically stable to zero by using the control law (13), while the control gainsktends to a negative constant,asttends to infinity.
For the hyperchaotic Liu system, the initial conditions of the master system and the salve system are chosen asx(0) = (15,22,?46,?21) andz(0) = (18,?13,?1,37), respectively. Selectγ1=5,γ2=10 and the initial conditions of the feedback gain byk1(0)=50,k2(0)=100. Figure 2 shows that the error states are asymptotically stable to zero by using the control law(15)while the control gainsk1andk2tend to two negative constants,respectively,asttends to infinity.

Fig.1. Adaptive synchronization for the Rikitake system.

Fig.2. Adaptive synchronization for the hyperchaotic Liu system.
5. Conclusion
In summary, we have studied the synchronization problem between two identical chaotic systems with less measurement and actuation. Under a weaker Lipschitz condition, a sufficient algebraic condition was proposed to guarantee the synchronization and meanwhile, an adaptive control scheme was designed to achieve the chaotic synchronization. The main result was proved by using the Lyapunov stability theory and Schur complementary lemma. Moreover, in most cases,this condition can be formulated as an LMI feasibility problem which can be efficiently solved by numerical tool. Our result generalized the results of Huang,[22]and also Guo[23](in a similar way). Finally, the result has been applied to the Rikitake system and the hyperhaotic Liu system and numerical simulations are also presented to verify the result.
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment?
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics?
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement?
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment?
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells?
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study?

