Jia-Bin Zhang(張嘉斌) Zhi-Xiang Jin(靳志祥) Shao-Ming Fei(費少明) and Zhi-Xi Wang(王志璽)

1School of Mathematical Sciences,Capital Normal University,Beijing 100048,China

2School of Physics,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: monogamy inequalities,polygamy inequalities,entanglement measures

1. Introduction

Quantum entanglement is a quintessential manifestation of the quantum mechanics. It is an essential feature of quantum mechanics which distinguishes the quantum from the classical world. While the entanglement in bipartite quantum systems has been intensively studied with rich understanding,the entanglement of multipartite quantum systems is less known in characterization and quantification. One interesting feature of multipartite entanglement is known as the monogamy of entanglement(MOE),[1,2]that is, the impossibility of sharing entanglement unconditionally among many subsystems of a composite quantum system. For example, for three two-level quantum systems, denoted byA,BandC,ifAandBare in a maximally entangled state,thenAcannot be entangled withCat all.

The first mathematical characterization of the MOE was expressed as a form of inequality for three-qubit state.[3]Osborne and Verstraete proved the Coffman–Kundu–Wootters (CKW) monogamy constraints for concurrence.[4]New classes of monogamy relations have been presented for other entanglement measures.[5–8]It has been shown that theαth power of concurrence and the convex-roof extended negativity(CREN)satisfy the monogamy inequalities in multiqubit systems forα ≥2,andα-th power of entanglement of formation(EoF),Tsallis-qentanglement and R′enyi-αentanglement show similar monogamy properties.[9–12]

Monogamy relations help people to understand the distribution of entanglement in multipartite systems. They also play an important role in the security analysis of quantum key distribution,[13]condensed-matter physics,[14]and even blackhole physics.[15]On the other hand, the assisted entanglement, which is a dual amount to bipartite entanglement measures, is also shown to have a polygamous of entanglement(POE). POE can be considered as another kind of entanglement constraints in multiparty quantum systems. A polygamy inequality was first established for arbitrary multiqubit systems by using the squared concurrence of assistance,[16,17]and it was generalized to multiqubit systems and arbitrary dimensional quantum systems in terms of various assisted entanglements.[18–20]POE is characterized by the polygamy inequality,Eα(ρA|BC)≤Eα(ρAB)+Eα(ρAC) for a tripartite quantum stateρABC, whereEα(ρA|BC) is the assisted entanglement[18]betweenAandBC. It provides an upper bound for the distribution of bipartite entanglement in a multipartite system.[16]

In recent years,tight classes of monogamy and polygamy inequalities of multiqubit entanglement using the non-negativeα-th power of various entanglement measures were also proposed.[10,18,21–25]In this paper,we optimize the monogamy and polygamy inequalities of multipartite entanglement for arbitrary quantum states, based on theα-th power of the multipartite qubit entanglement. Furthermore, we show that our optimized monogamy and polygamy relations are tighter inequalities than the results in Refs.[10,16–18,21–26].

2. Optimized relations for concurrence

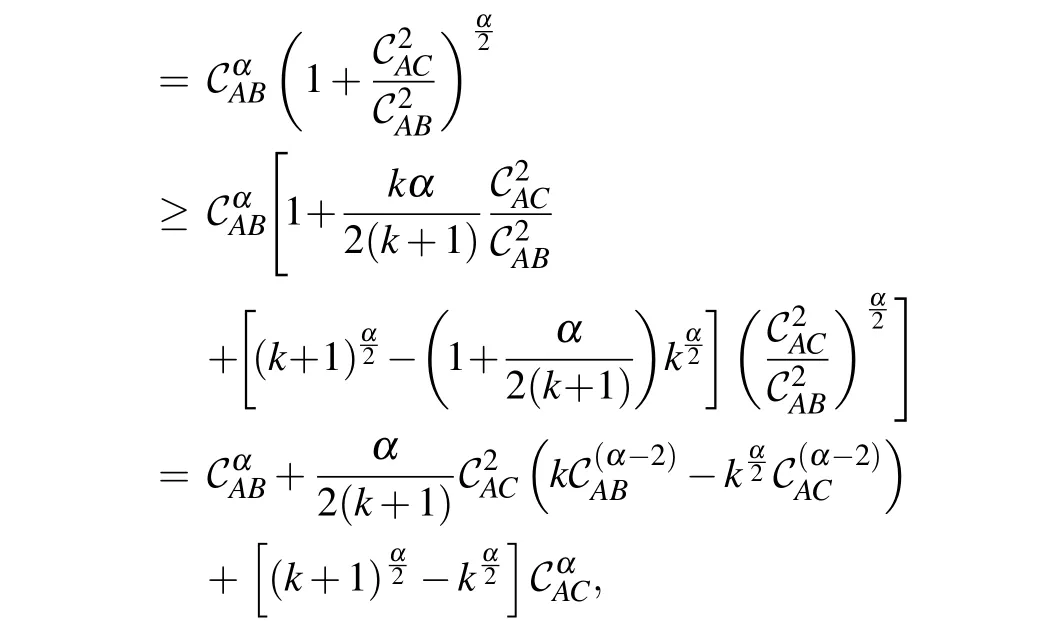
where the second inequality is due to inequality(3).

Note Lemma 2.1 shows that there exits a new trade-off relation among subsystemsA,BandCof a composite quantum system, i.e., the entanglement shared among subsystemsA,BandCis restricted by inequality(4).

In term of Lemma 2.1,we get a new general monogamy relation of concurrence forρAB1···BN?1.

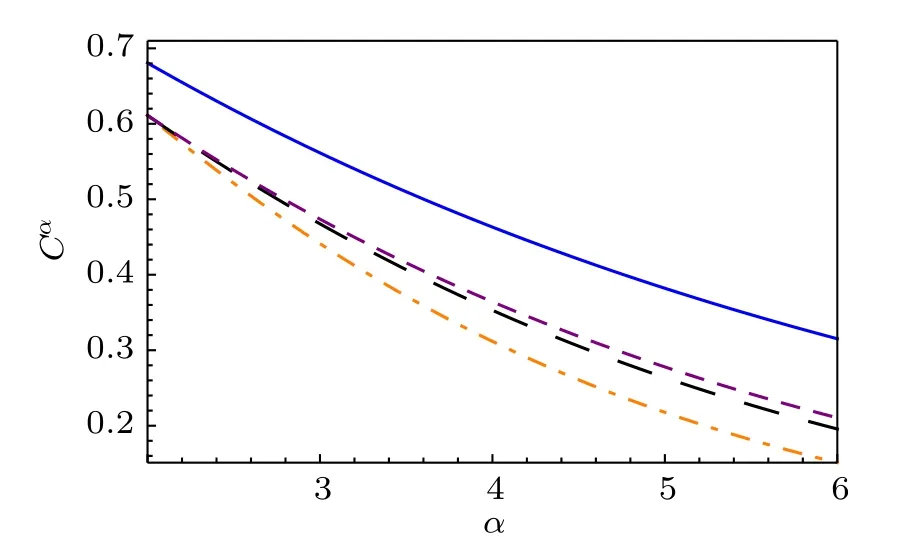
Fig. 1. The axis Cα stands for the α-th power concurrence of |ψ〉. The blue solid line represents the concurrence of|ψ〉in Example 2.1. The black dotted(purple dashed)line represents the lower bound from our result when k=2(k=3), while the orange dotdashed line represents the lower bound from the corresponding result r=0.5 in Ref.[22].

In order to discuss the polygamy relations of the concurrence of assistance(CoA)CaA|B1···BN?1,we need the following inequality.[25]For 0≤x ≤1/k,k ≥1 and 0≤μ ≤1,

where the second inequality is due to inequality(10).

Note Lemma 2.2 shows that there exits another trade-off relation among subsystemsA,BandCof a composite quantum system,namely polygamy relation,the information shared amongA,BandCis restricted by the inequality(11).

Associated with the Lemma 2.2,we obtain the following two new polygamy relations.

Proof By partitioning the last qubit systemBiBi+1···BN?1(i= 1,2,...N ?2) into two subsystems and using the above inequality(11)repeatedly,one gets the result.

The Propositions 2.3 and 2.4 show that the new polygamy inequalities (12) and (13) are tighter than (18) and (19) in Ref.[22]. Let us illustrate this by an example.

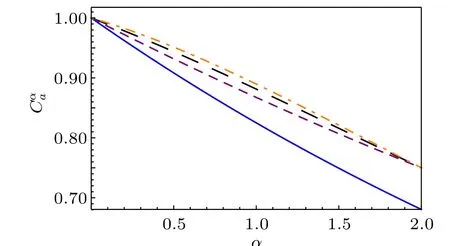
Fig.2.The axis Cαa stands for the αth power CoA of|ψ〉.The blue solid line represents the upper bound of concurrence of|ψ〉in Example 2.2,the orange dotdashed line represents the upper bound of polygamy of CoA in Ref.[22],the the black dotted (purple dashed) line represents the upper bound from our result when k=2(k=3).

3. Optimized relations for entanglement negativity

Fig.3. The axis Nc is the CREN of|ψ〉. The blue solid line represents the CREN of|ψ〉in Example 3.1. The black dotted(purple dashed)line represents the lower bound from our result for k=2(k=3). The green dashed line represents the lower bound from the result(k=0.5)in Ref.[22].

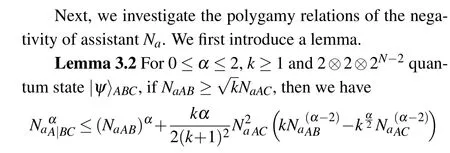
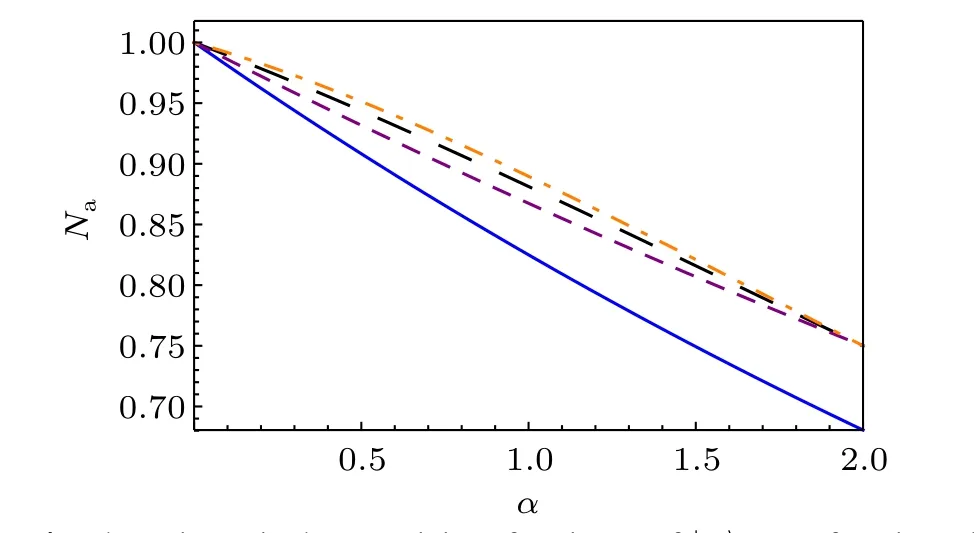
Fig. 4. The axis Na is the negativity of assistant of |ψ〉, as a function of α. The blue solid line represents the negativity of|ψ〉in Example 3.1. The black dotted(purple dashed)line represents the lower bound from our result for k=2(k=3). The orange dotdashed line represents lower bound from the result(k=0.5)in Ref.[22].

4. Optimized relations for EoF and EoA

The EoF[35,36]is a well defined important measure of entanglement for bipartite systems. Let HAand HBbemandndimensional(m ≤n)vector spaces, respectively. The EoF of a pure state|ψ〉AB ∈HA ?HBis defined by

Proof The proof is similar to the prove of Lemma 4.1.

NoteEA|BCstands for the EoF of the stateρABC, which quantifies the entanglement between the subsystemsA,BandC. Lemma 4.1 implies that there exits restrictive condition among the subsystemsA,BandCwhen they sharing information.

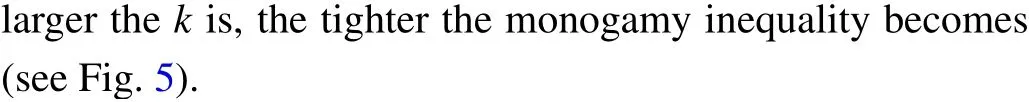
Fig.5. EoF as a function of α. The blue solid line represents the EOF of the state|ψ〉in Example 4.1. The black dotted(purple dashed)line represents the lower bound from our result for k=2 (k=3). The orange dotdashed line represents the lower bound from the corresponding result (k=0.5) in Ref.[22].

by using the inequality (10) and iterating inequality (37) on the last term of inequality(39),we obtain the result.

Proposition 4.2 implies that polygamy inequality (38)tightens again the upper bounds ofEa(ρA|B1···BN?1) given in Ref.[22].

5. Optimized relations for Tsallis entanglement

where the first inequality is due to thatgq(x)is a convex function. The second inequality is due to the Cauchy–Schwarz inequality. In terms of the definition of Tsallis-qentanglement and thatgq(x)is a monotonically increasing function,we obtain the third inequality. Therefore,we have

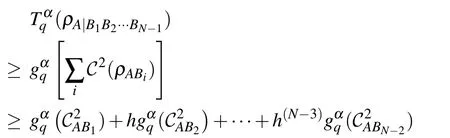
Fig. 6. The axis T2 is the Tsallis-q (q=2) entanglement of |ψ〉, which is functions of α. The blue solid line represents the lower bound of the Tsallis-q of|ψ〉(q=2)in Example 5.1. The black dotted(purple dashed)line represents the lower bound from our result for k=2 (k=3). The orange dotdashed line represents the lower bound from the result(k=0.5)in Ref.[22].

Next, we investigate the polygamy relations of the Tsallis-qentanglement of assistant (ToA). Firstly, we introduce a new polygamy relation of mixed stateρABCas follows.

6. Conclusion

Multipartite entanglement is of particular significance in quantum information processing. Monogamy and polygamy relations characterize the multipartite entanglement distributions among the subsystems. Using theα-th power of the bipartite entanglement, we have presented new monogamy and polygamy inequalities related to theαth power of concurrence, EoF, CREN and Tsallis-qentanglement, which are tighter than the existing entanglement monogamy and polygamy inequalities.[22–24,26]Our approach may be also applied to the investigation on monogamy and polygamy inequalities of other entanglement measures.