A NEW ALGORITHM FOR MONOTONE INCLUSION PROBLEMS AND FIXED POINTS ON HADAMARD MANIFOLDS WITH APPLICATIONS?
(張石生)
Center for General Education,China Medical University,Taichung 40402,Taiwan,China E-mail:changss2013@163.com
Jinfang TANG (唐金芳)
Department of Mathematics,Yibin University,Yibin 644007,China E-mail:jinfangt 79@163.com
Chingfeng WEN (溫慶豐)
Department of Medical Research,Kaohsiung Medical University Hospital,Kaohsiung 80708,Taiwan,China E-mail:cfwen@kmu.edu.tw
Abstract In this article,we propose a new algorithm and prove that the sequence generalized by the algorithm converges strongly to a common element of the set of fixed points for a quasi-pseudo-contractive mapping and a demi-contraction mapping and the set of zeros of monotone inclusion problems on Hadamard manifolds.As applications,we use our results to study the minimization problems and equilibrium problems in Hadamard manifolds.
Key words Monotone inclusion problem;quasi-pseudo-contractive mapping;demi-contraction mapping;maximal monotone vector field;quasi-nonexpansive mappings;Hadamard manifold
1 Introduction
Rockafellar[1]considered the inclusion problem of finding

B
is a set-valued maximal monotone mapping de fined on a Hilbert spaceH
.He developed an elegant method,known as the proximal point algorithm(PPA),to solve this inclusion problem.During the last two decades,inclusion problem(1.1)has been extended and generalized in many directions because of its applications to different areas in science,engineering,management and the social sciences(see,for example,[2–9]and the references therein).
Recently,many convergence results attained by the proximal point algorithm have been extended from the classical linear spaces to the setting of manifolds(see,for examle,[10–14]).Li et al.[10]developed the proximal point method for problem(1.1)in the setting of Hadamard manifolds.Later,Li et al.[11]extended the Mann and Halpern iteration scheme for finding the fixed points of nonexpansive mappings from Hilbert spaces to Hadamard manifolds.Very recently,Ansari et al.[12]and Al-Homidan-Ansari-Babu[13]considered the problem of finding
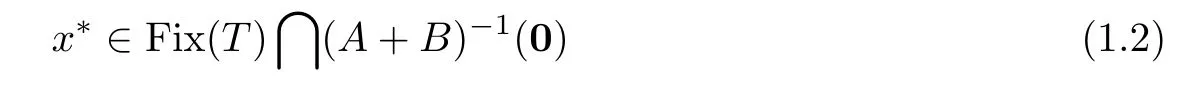
T
is a nonexpansive mapping,B
is a set-valued maximal monotone mapping,andA
is a single-valued continuous and monotone mapping.They proposed some Halpern-type and Mann-type iterative methods.They proved that,under suitable conditions,the sequence generated by the algorithm converges strongly to a common element of the set of fixed points of the mappingT
and the set of solutions of the inclusion problem.Motivated and inspired by the works in[5–8]and[11–14],in this article we consider the problem of finding
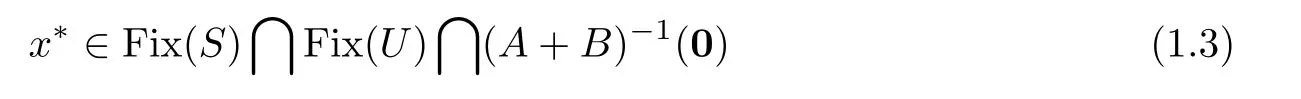
S
is a quasi-pseudo-contractive mapping,U
is a demi-contractive mapping,B
is a set-valued maximal monotone mapping andA
is a singlevalued and monotone mapping such thatA
+B
is maximal monotone.We propose a new type of algorithm and prove that the sequences generalized by the algorithm converge strongly to a common element of problem(1.3).As applications we apply our results to study the minimization problems and equilibrium problems in Hadamard manifolds.2 Preliminaries

p,q
)is the minimal length over the set of all such curves joiningp
toq
,which induces the original topology onM
.A Riemannian manifoldM
is complete if,for anyp
∈M
,all geodesics emanating fromp
are de fined for allt
∈R.A geodesic joiningp
toq
inM
is said to be a minimal geodesic if its length is equal to d(p,q
).A Riemannian manifoldM
equipped with Riemannian distance d is a metric space(M,
d).By the Hopf-Rinow Theorem[15],ifM
is complete,then any pair of points inM
can be joined by a minimal geodesic.Moreover,(M,
d)is a complete metric space and bounded closed subsets are compact.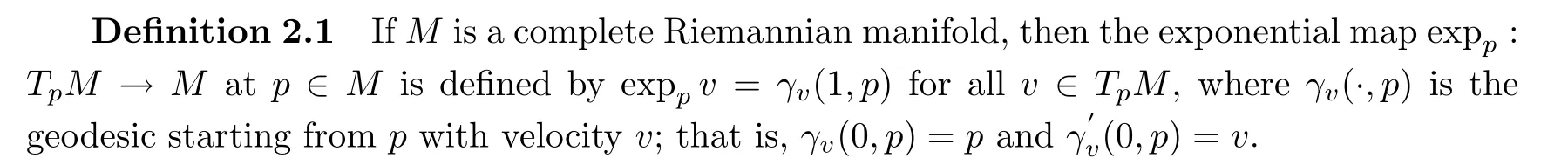
tv
=γ
(t,p
)for each real numbert
.It is easy to see that exp0=γ
(0,p
)=p
,where 0 is the zero tangent vector.Note that the exponential map expis differentiable onT
M
for anyp
∈M
.De finition 2.2
A complete simply connected Riemannian manifold of non-positive sectional curvature is called a Hadamard Manifold.Proposition 2.3
([15])LetM
be a Hadamard manifold.Then,for any two pointsx,y
∈M
,there exists a unique normalized geodesicγ
:[0,
1]→M
joiningx
=γ
(0)toy
=γ
(1)which is in fact a minimal geodesic denoted by
The following inequalities can be proved easily:
Lemma 2.4
LetM
be a finite dimensional Hadamard manifold.(i)Letγ
:[0,
1]→M
be a geodesic joiningx
toy
.Then we have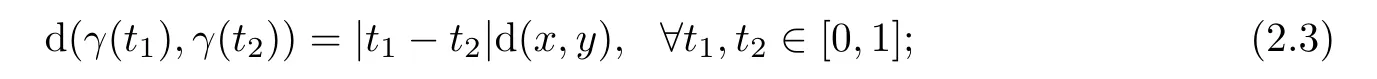
x,y
)denotes the Riemannian distance).(ii)For anyx,y,z,u,w
∈M
andt
∈[0,
1],the following inequalities hold: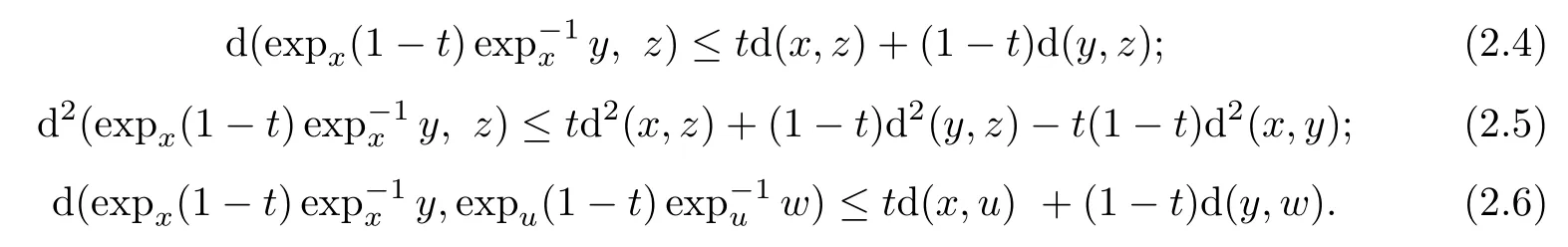
M
be a Hadamard manifold.A subsetC
?M
is said to be geodesic convex if,for any two pointsx
andy
inC
,the geodesic joiningx
toy
is contained inC
.In the sequel,unless otherwise speci fied,we always assume thatM
is a finite dimensional Hadamard manifold,andC
is a nonempty,bounded,closed and geodesic convex set inM
,and Fix(S
)is the fixed point set of a mappingS
.A functionf
:C
→(?∞,
∞]is said to be geodesic convex if,for any geodesicγ
(λ
)(0≤λ
≤1)joiningx,y
∈C
,the functionf
?γ
is convex,that is,
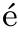
De finition 2.7
A mappingS
:C
→C
is said to be(1)contractive if there exists a constantk
∈(0,
1)such that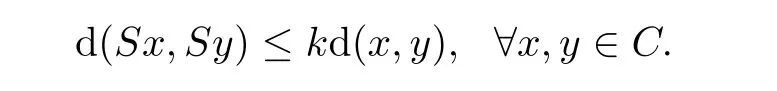
k
=1,thenS
is said to be nonexpansive,and(2)quasinonexpansive if Fix(S
)/=?and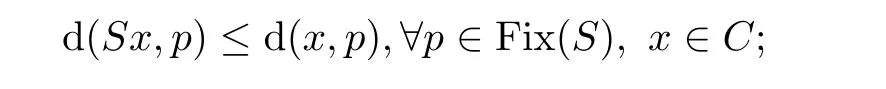
x,y
∈C
,the functionφ
:[0,
1]→[0,
∞]de fined by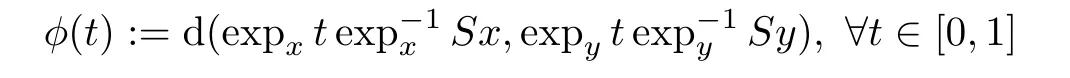
is nonincreasing;
(4)k
-demicontractive[19]if Fix(S
)/=?and there exists a constantk
∈[0,
1)such that
S
)/=?and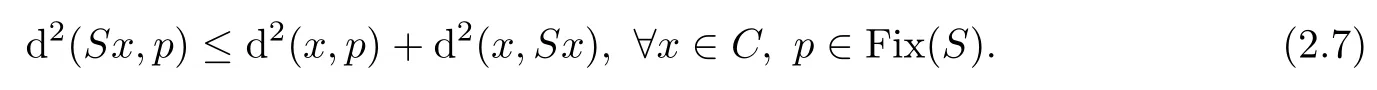
Proposition 2.8
([18])LetS
:C
→C
be a mapping.Then the following statements are equivalent:(i)S
is firmly nonexpansive;(ii)for anyx,y
∈C
andt
∈[0,
1]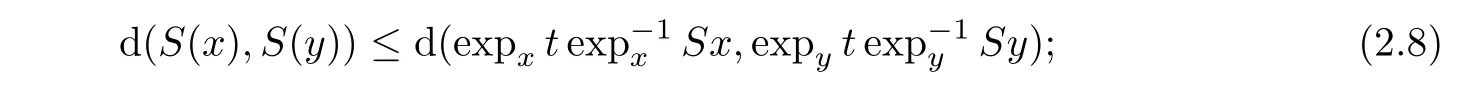
x,y
∈C
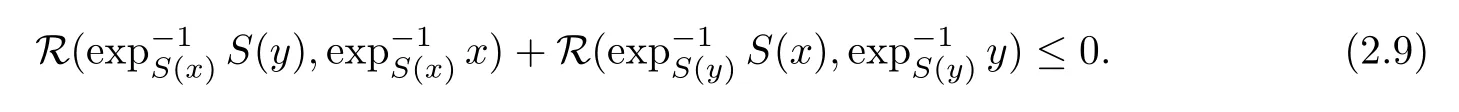
Lemma 2.9
IfS
:C
→C
is a firmly nonexpansive mapping and Fix(S
)/=?,then for anyx
∈C
andp
∈Fix(S
),the following conclusion holds:
Proof
For given pointsx
∈C,p
∈Fix(S
)andSx
,we consider a geodesic triangle△(p,Sx,x
).By a comparison theorem for triangle([15]Proposition 4.5),we have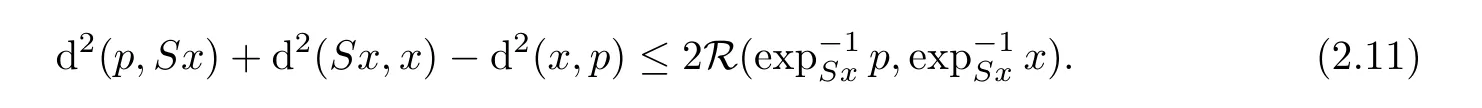
S
:C
→C
is firmly nonexpansive,takingy
=p
in(2.9),we have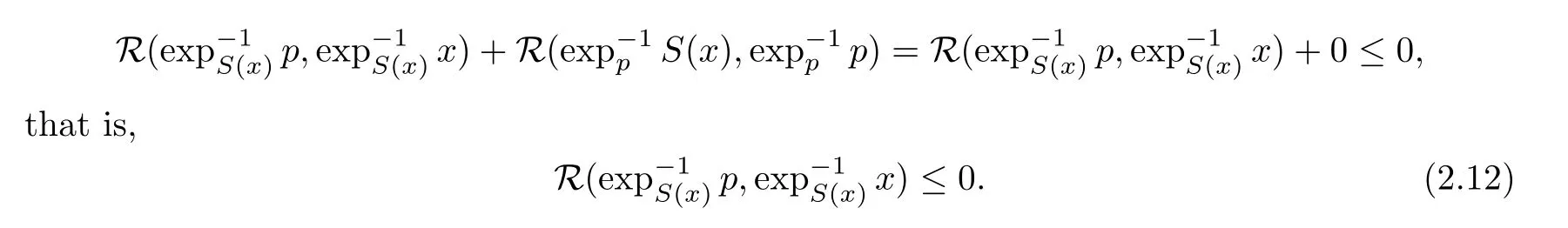
This,together with(2.11),shows that
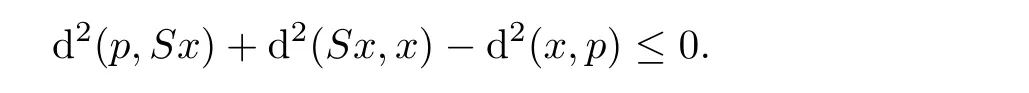
The conclusion of Lemma 2.9 is proved.
Remark 2.10
From De finition 2.7 and Lemma 2.9,it is easy to see that if Fix(S
)/=?,then the following implications hold: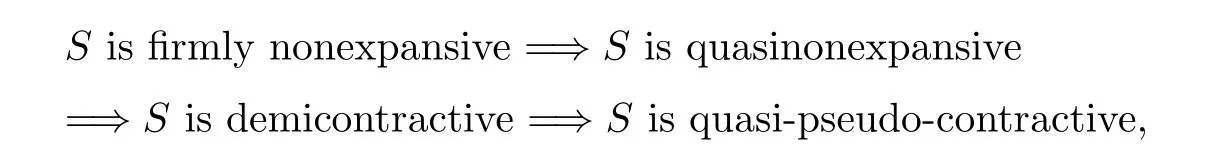
S
)/=?andS
is firmly nonexpansive,then,by(2.10),it is quasi-nonexpansive;therefore it is demicontractive and so it is quasi-pseudo-contractive.These show that the class of quasi-pseudo-contractive mappings is more general than the classes of quasinonexpansive mappings,firmly nonexpansive mappings andk
-demicontractive mappings.In the sequel,we denote by X(M
)the set of all set-valued vector fieldsA
:M
?TM
such thatA
(x
)?T
M
for allx
∈M
,and we let the domain D(A
)ofA
be de fined by D(A
)={x
∈M
:A
(x
)/=?}.De finition 2.11
A set-valued vector fieldA
∈X(M
)on a Hadamard manifoldM
is said to be(1)monotone if,for anyx,y
∈D(A
),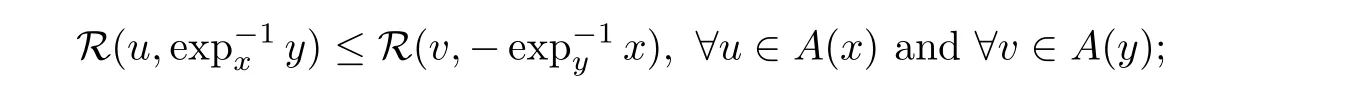
x
∈D(A
)andu
∈T
M
,the condition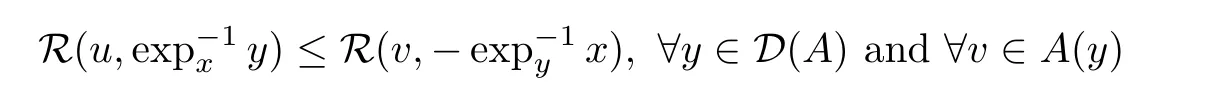
u
∈A
(x
);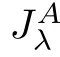
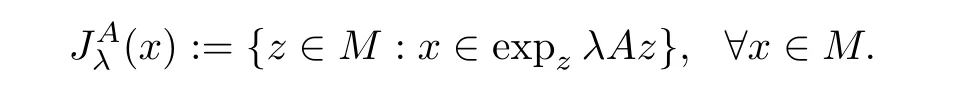
A
of orderλ>
0.
De finition 2.13
A mappingT
:C
→C
is said to be demiclosed at 0 if,for any sequence{x
}?C
such thatx
→x
and d(x
,Tx
)→0,thenx
∈Fix(T
).3 Main Results
First we give following Lemma,which will be needed in proving our main result:
Lemma 3.1
LetM
be a Hadamard manifold andT
:C
→C
be a mapping which isL
-Lipschitzian(L
≥1)and demiclosed at 0.LetG
:C
→C
andK
:C
→C
be two mappings de fined by
T
)=Fix(T
?G
)=Fix(K
);(2)K
is also demiclosed at 0;(3)K
:C
→C
isL
-Lipschitzian;(4)In addition,ifT
:C
→C
is quasi-pseudo-contractive,thenK
:X
→X
is a quasinonexpansive mapping,that is,for anyx
∈C
andp
∈Fix(K
)(=Fix(T
)),
T
:C
→C
isk
-demi-contractive andk
∈(0,
1),then the mappingW
:C
→de fined by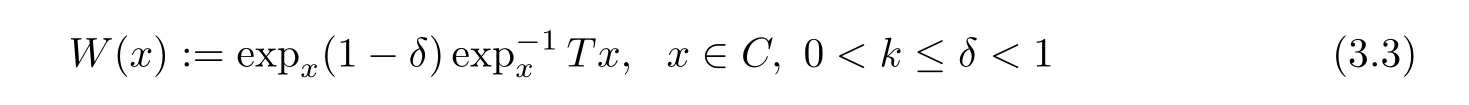
has the following properties:
(a)Fix(T
)=Fix(W
);(b)W
isL
-Lipschitzian;(c)W
is demiclosed at(0);(d)W
is a quasi-nonexpansive mapping.Proof
First we prove the conclusion(1)In fact,ifu
∈Fix(T
),then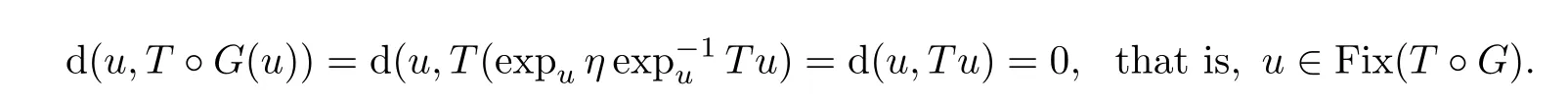
u
∈Fix(T
?G
),then it follows from(2.4)that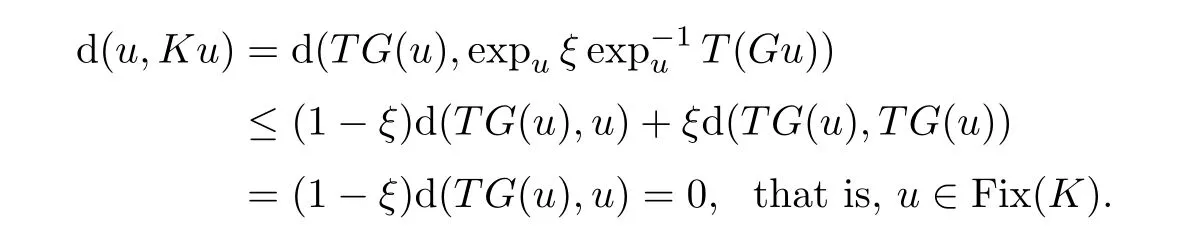
u
∈Fix(K
),then,from(2.4),we have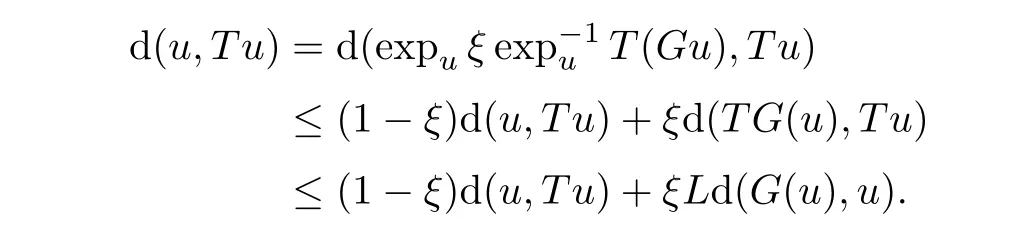
Simplifying,we have

Lη<
1,this implies thatu
∈Fix(T
).The conclusion(1)is proved.Now we prove the conclusion(2)
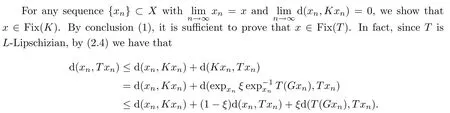
Simplifying,we have

This implies that
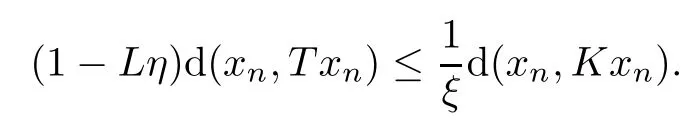
Lη
)>
0 and d(x
,Kx
)→0,this implies that d(x
,Tx
)→0.SinceT
is demiclosed at 0,x
∈Fix(T
).Hencex
∈Fix(K
);that is,K
is demiclosed at 0.Next we prove the conclusion(3)
SinceT L
-Lipschitzian,for anyx,y
∈C
it follows from(2.6)that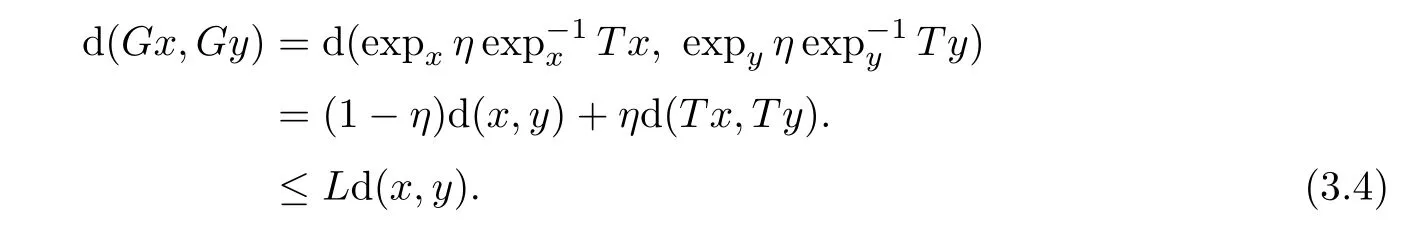
Similarly,from(2.6)and(3.4),we have

Now we prove the conclusion(4)
For anyp
∈Fix(T
)and anyx
∈X
,it follows from(2.5)that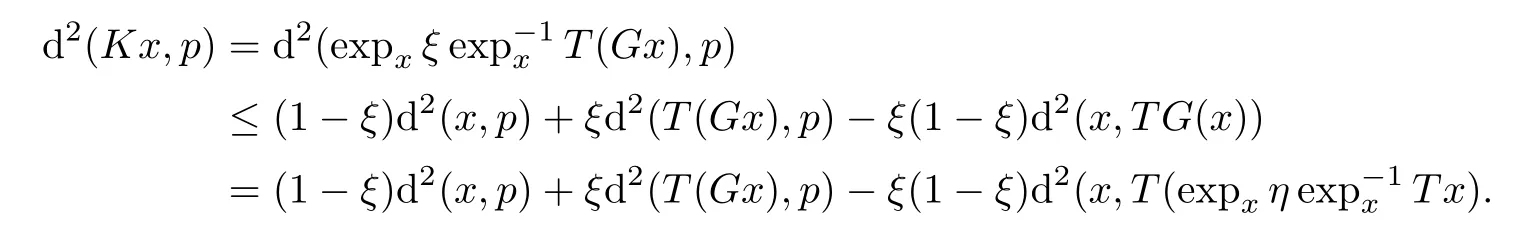
T
is quasi-pseudo-contractive,we have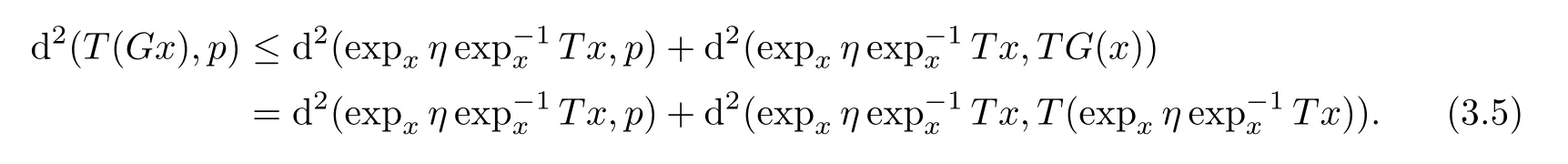
From(2.5)we have
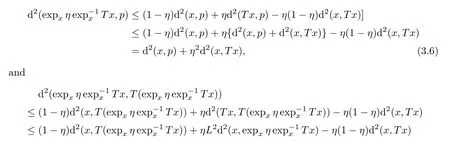
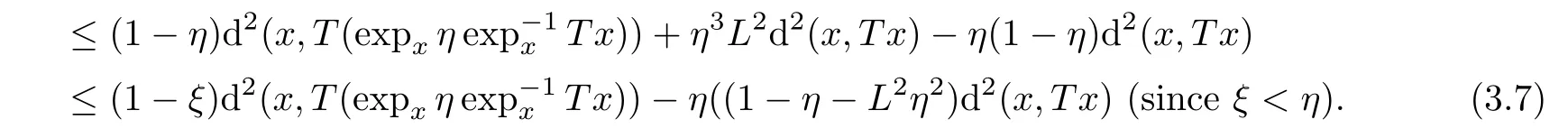
Substituting(3.6)and(3.7)into(3.5),after simplifying,we have
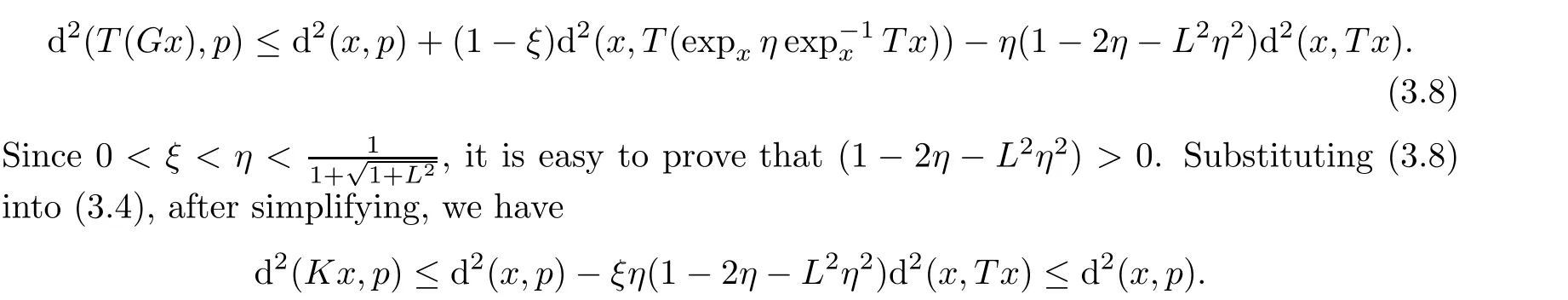
Finally we prove the conclusion(5)
It is easy to prove thatW
has the properties(a)–(c).Next we prove thatW
has the property(d).In fact,since Fix(T
)=Fix(W
),for anyp
∈Fix(T
)=Fix(W
)andx
∈C
it follows from(3.3),(2.5)and the de finition ofk
-demicontractive mapping that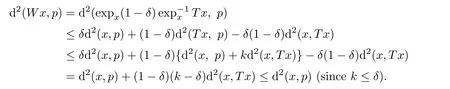
The conclusion(d)is proved.Therefore the proof of Lemma 3.1 is completed.
In the sequel,we always assume that
(1)M
is a finite dimensional Hadamard manifold andC
is a nonempty closed and bounded geodesic convex subset ofM
;(2)B
:C
?TM
is a set-valued maximal monotone mapping andA
:C
→TM
is a single-valued and monotone mapping such thatA
+B
is a set-valued maximal monotone vector field;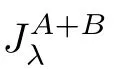
S
:C
→C
is a quasi-pseudo-contractive mapping,U
:C
→C
is ak
-demi-contractive mapping,k
∈(0,
1),and thatS
andU
both are demiclosed at 0 andL
-Lipschitzian,L
≥1;(5)We can letG
,K
:C
→C
andK
:C
→C
be the mappings de fined by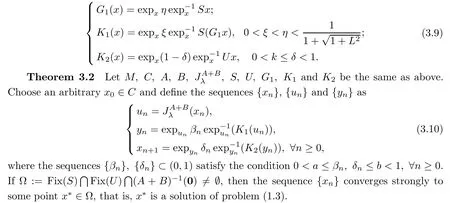
Proof
(I)First we observe that by the assumptions of Theorem 3.2,Lemma 2.12 and Lemma 3.1,we have that
K
is quasi-nonexpansive,from Lemma 2.4 and(3.11)we have that
Similarly,from Lemma 2.4 and(3.12),we have
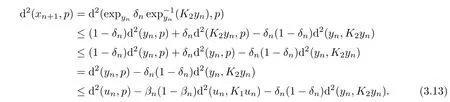
This implies that

In fact,it follows from(3.13)that
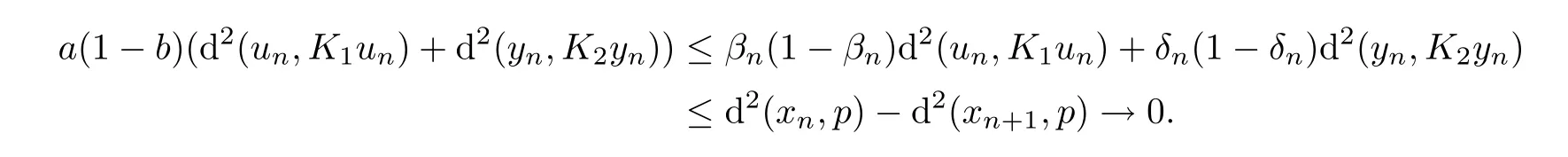
a
(1?b
)>
0,this implies that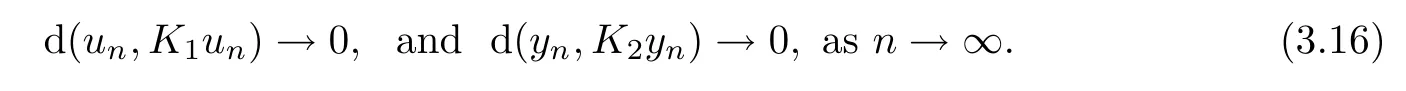
From(3.16)and Lemma 2.4,we have
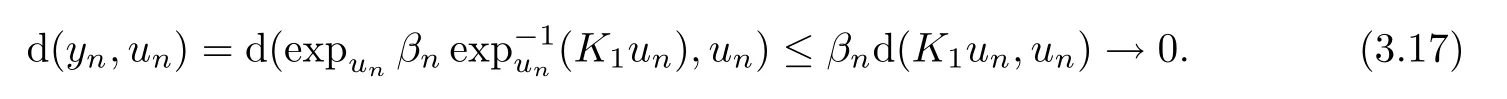
p
∈?,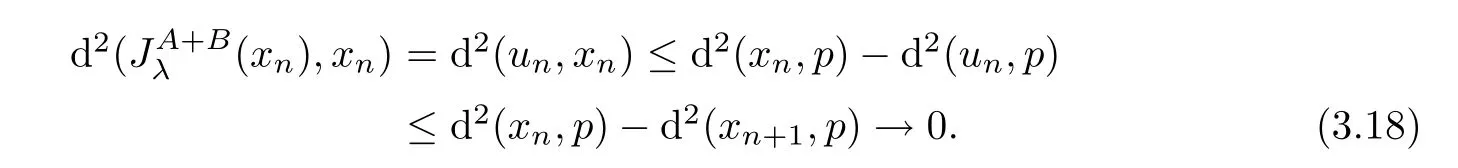
The conclusion of(3.15)is proved.
(IV)Now we prove that{x
}converges strongly to some point in ?.
This completes the proof of Theorem 3.2.
4 Applications
Throughout this section we assume thatM
is a finite dimensional Hadamard manifold,and thatC
is a bounded closed and geodesic convex subset ofM
.4.1 Minimization problems on Hadamard manifolds
Letf
:M
→(?∞,
+∞]be a proper,lower semicontinuous and geodesic convex function.Consider the minimization problem of finding a pointx
∈M
such that
We denote by ?the solution set of the minimization problem(4.1),that is,
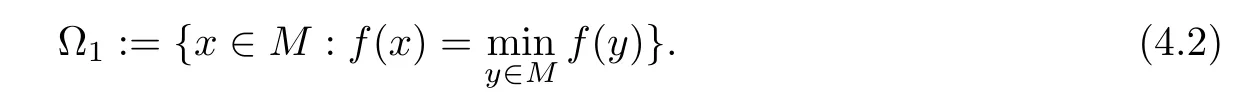
?f
(x
)off
atx
∈M
[21]is de fined by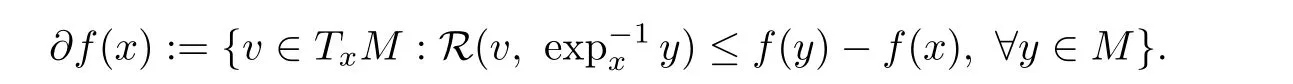
Lemma 4.1
([10])Letf
:M
→(?∞,
+∞]be a proper,lower semicontinuous and geodesic convex function.Then,the subdifferential?f
off
is a maximal monotone vector field,and
f
:M
→(?∞,
+∞],i
=1,
2,
is a proper,lower semicontinuous and geodesic convex function,and?f
is the subdifferential off
,so?
(f
+f
)=?f
+?f
and?
(f
+f
)is a maximal monotone vector field.Hence,from Theorem 3.2 and Lemma 4.1,we have the following result:
β
},
{δ
}?(0,
1)such that 0<a
≤β
,δ
≤b<
1,
?n
≥0 andK
andK
are mappings de fined by(3.9).If
x
}converges strongly to some pointx
∈?.In particular,ifS
=U
=I
(the identity mapping onM
)andf
=f,f
=0,then the sequence{x
}de fined by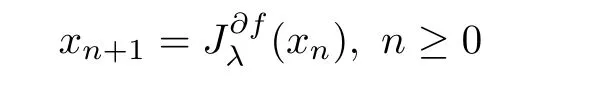
converges strongly to a solution of minimization problem(4.1).
4.2 Equilibrium problems on Hadamard manifolds
LetF
:C
×C
→R be a bifunction.We assume that the following conditions are satis fied: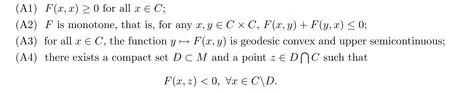
x
∈C
such that
The solution set of equilibrium problem(4.5)is denoted by EP(F).

Lemma 4.4
([13])LetC
be a nonempty closed and geodesic convex subset of a Hadamard manifoldM
.LetF
:C
×C
→R be a bifunction satisfying the conditions(A1)–(A4).LetH
:M
?TM
be a set-valued mapping de fined by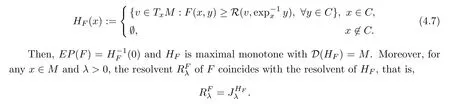
B
=H
,A
=0 andS
=U
=I
,the following result can be obtained from Theorem 3.2 immediately:Theorem 4.5
LetF
:C
×C
→R be a bifunction satisfying the conditions(A1)–(A4)and letH
:M
→M
be the mapping de fined by(4.7).For any givenx
∈C
,let{x
}be the sequence de fined by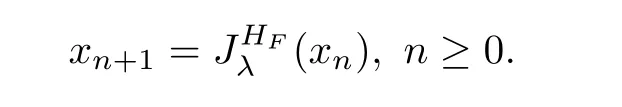
EP
(F
)/=?,then the sequence{x
}converges strongly to a solution of equilibrium problem(4.5).5 Conclusion
In this paper,an iterative algorithm to approximate a common element of the set of fixed points of a quasi-pseudo-contractive mapping and a demi-contraction mapping and the set of zeros of monotone inclusion problems on Hadamard manifolds has been proposed.Under suitable conditions,we proved that the sequence generated by the algorithm converges strongly to a common solution of problem(1.3).Since the quasi-pseudo-contractive mapping and the demicontractive mapping is more general than the nonexpansive mapping,firmly nonexpansive mapping and quasi-nonexpansive mapping,problem(1.3)studied in our paper is quite general.It includes many kinds of problems,such as convex optimization problems,the fixed point problem,variational inclusion problems,and equilibrium problems as its special cases.Therefore the results presented in the paper not only improve and generalize some recent results,but also provide a powerful tool for solving other problems related to(1.3).
 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
