Li Haohao

(School of Data Sciences, Zhejiang University of Finance and Economics,Hangzhou 310018, China)

Abstract：In this paper the scheduling problem Rm||Cmax is cast in a privacy-preserving framework. Consider the situation that the parameters in problem Rm||Cmax are partitioned into groups. Each group is owned by a distinct private entity that is unwilling to share or make public its own data. We construct a secure program based on the privately held data without revealing it by employing random matrix transformation. The secure program has the same optimal minimum value as the original mixed 0-1 linear program model of the problem Rm||Cmax, and the optimal solution to the secure program is publicly generated and is available to all entities. The 0-1 components in optimal solution to the secure program are coincident to those in optimal solution to the original solution.

Keywords： scheduling, 0-1 programming, privacy-preserving, secure program

1 Introduction

Recent interest in privacy-preserving classification and computation, wherein the data to be classified is owned by different entities that are unwilling to reveal the data they hold or make it public, has spread to the field of optimization[1]. In this work we deal with a privacy-preserving scheduling problem.

The scheduling problem ofRm||Cmaxis discussed widely which schedulesnjobs onmunrelated parallel machines with the objective of minimizing the makespan, i.e.,the total timespan required to process all the given tasks. Each jobjhas a processing requirementpijwhich depends on the machineijobjwill be processed on. In reality, the machines may be partitioned into groups where the processing information of different jobs depending on each group is owned by a distinct entity. Each entity is unwilling to share its information data to the others.

In this paper we considered about the unrelated parallel machine scheduling problem mentioned above, and propose a privately held solution method by recasting the original privacy-preserving problem into a public one.

2 Problem formulation

Considering about scheduling model on unrelated parallel machines to minimize makespan, it can be simply thought of a 0-1 linear programming problem. If let LetP=(pij)m×n. Suppose that the matrixPis divided intopblocks ofm1,m2,···,mp,n-dimensional rows withm1+m2+···+mp=m. Each block of rows of matrixPcorresponding to the index setsI1,I2,··· ,Ipis owned by a distinct entity that is unwilling to make this block of data public or share it with other entities. We wish to solve this scheduling problem without revealing any privately held data.

The constraints in problem (3) can be separated into two parts, the privacy ones and the public ones. Recast the problem (3) into matrix notation we have

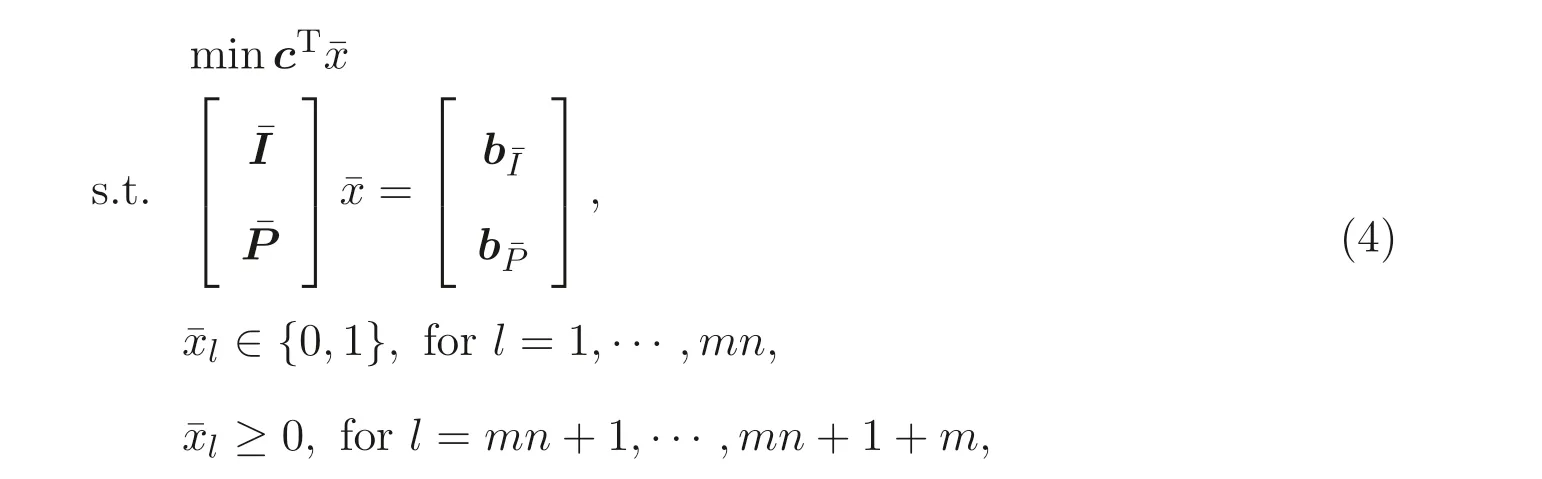
where

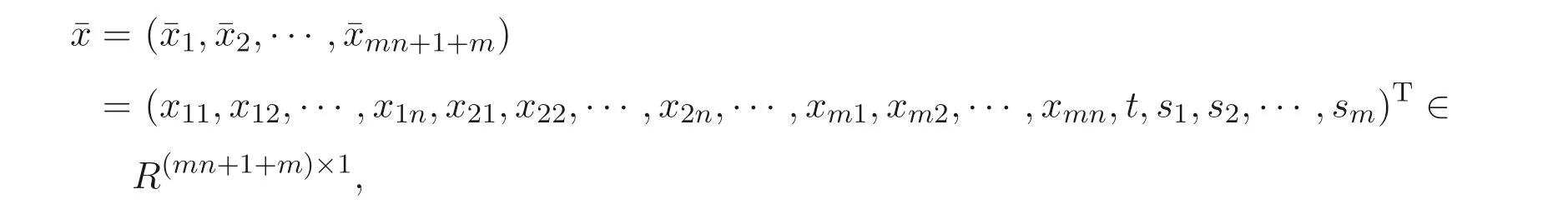
in whichs1,s2,··· ,smare slack variables,

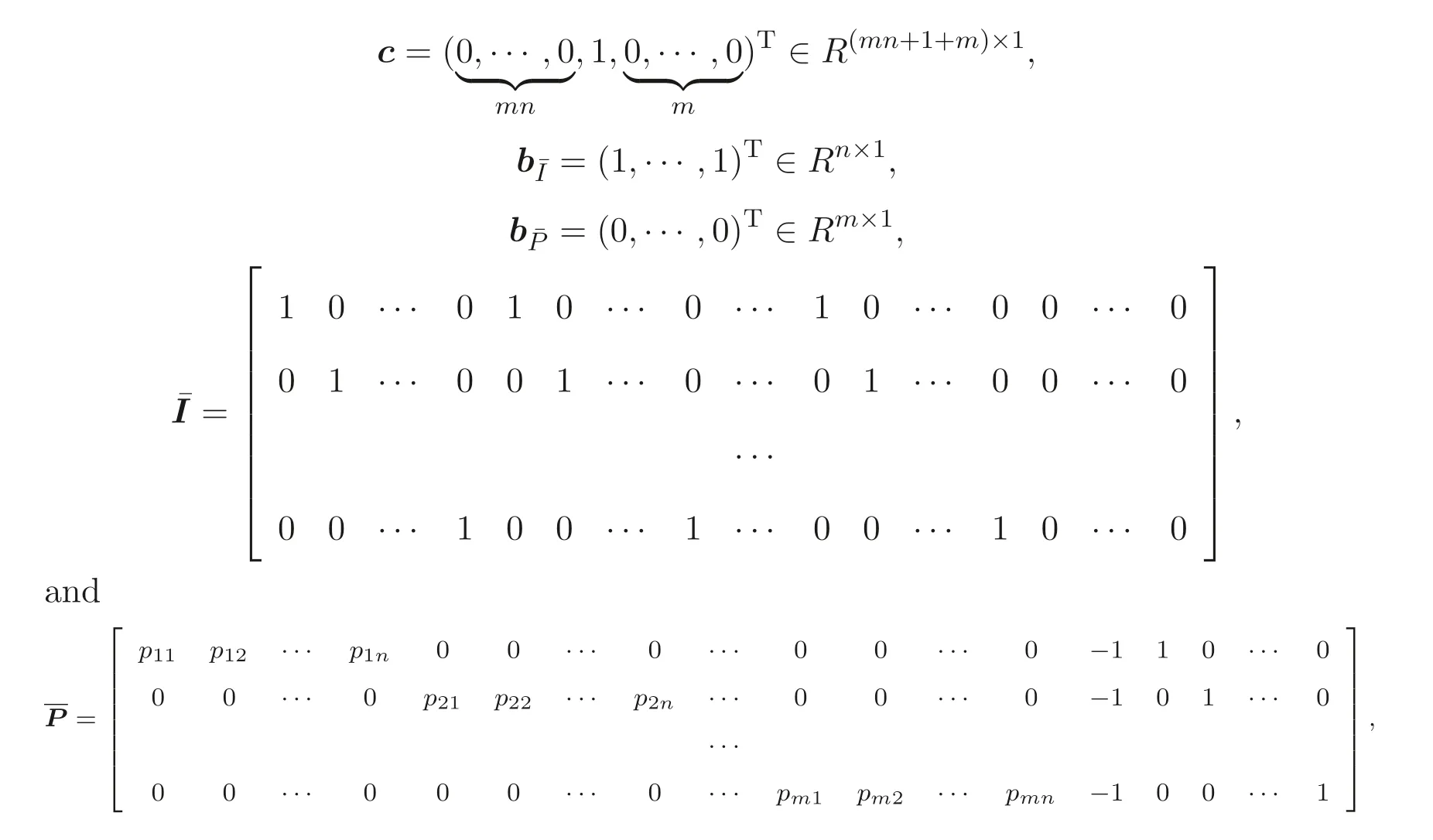
According to our knowledge, this kind of problem, optimization of a privacypreserving mixed linear 0-1 program,has not been solved so far and it is a very demanding problem. References[2-5]presented some efficient algorithms based on transformation techniques methods for privacy-preserving linear programming problems. Using those methods,the user is no longer bound to use simplex,but can take advantage of the all improvements to linear-programming algorithms, e.g., interior point methods and some newly proposed effective algorithms for linear optimization[6-7]. However, their methods cannot be used for the proposed problem in this paper because the proposed problem is confronted with 0-1 variables.

3 Problem solving

In this section,we propose a solution method for this privacy-preserving scheduling model, based on a random transformation technique, which was first used for privacypreserving linear programming model with inequality constraints[2]. However, this technique is not applicable directly to model(4), otherwise the 0-1 variables will reveal the private data.

It is useful to discuss more on model (4). Note that for a real variablex, the conditionx ∈{0,1}is equivalent to the equationx(x ?1) = 0. Thus, the privacypreserving scheduling model (4) is reformulated equivalently as

Better, he said to himself, trust to a thread than to the mercies of a king; and, gliding26 down, he found himself safe on the other side of the wall

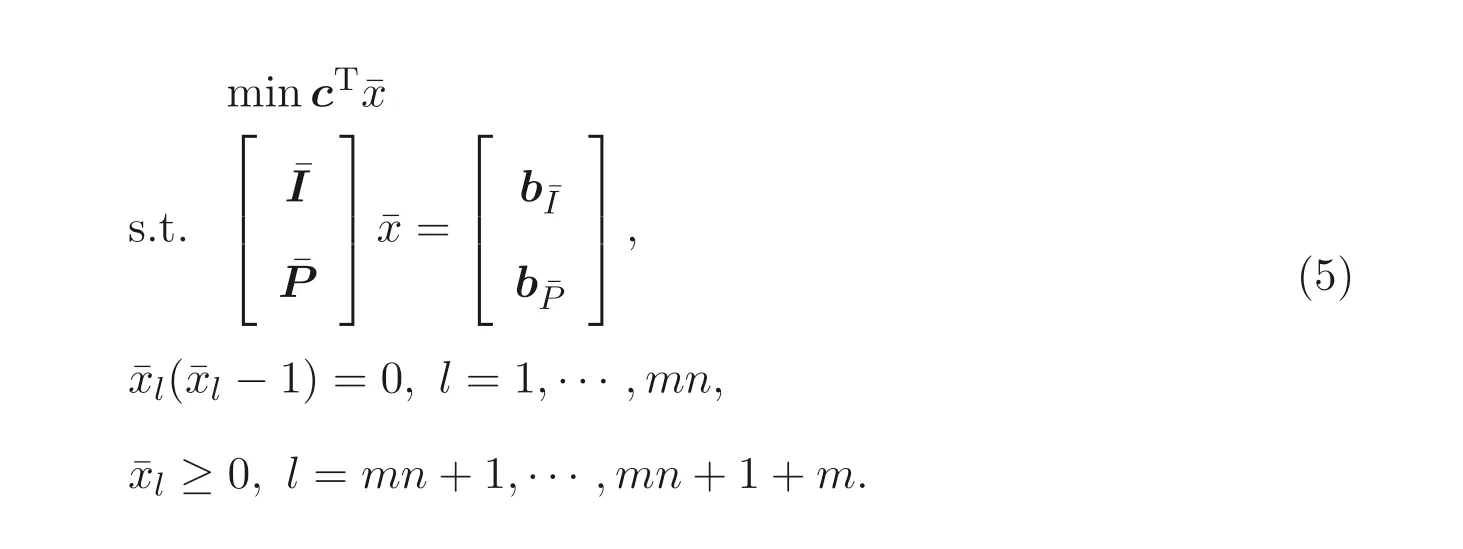
To keep the privacy,each of entityIichooses its own privately held random matrixBIi ∈Rk×miwithk ≥m+n(i=1,··· ,p) and random numbers

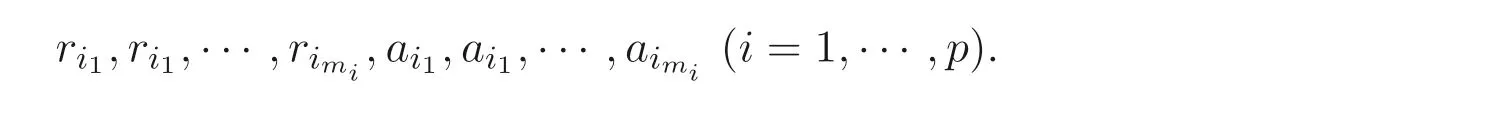
where

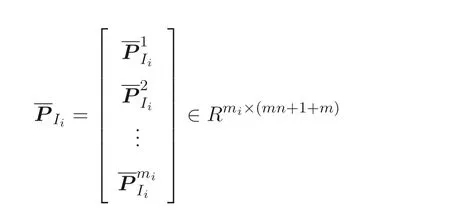
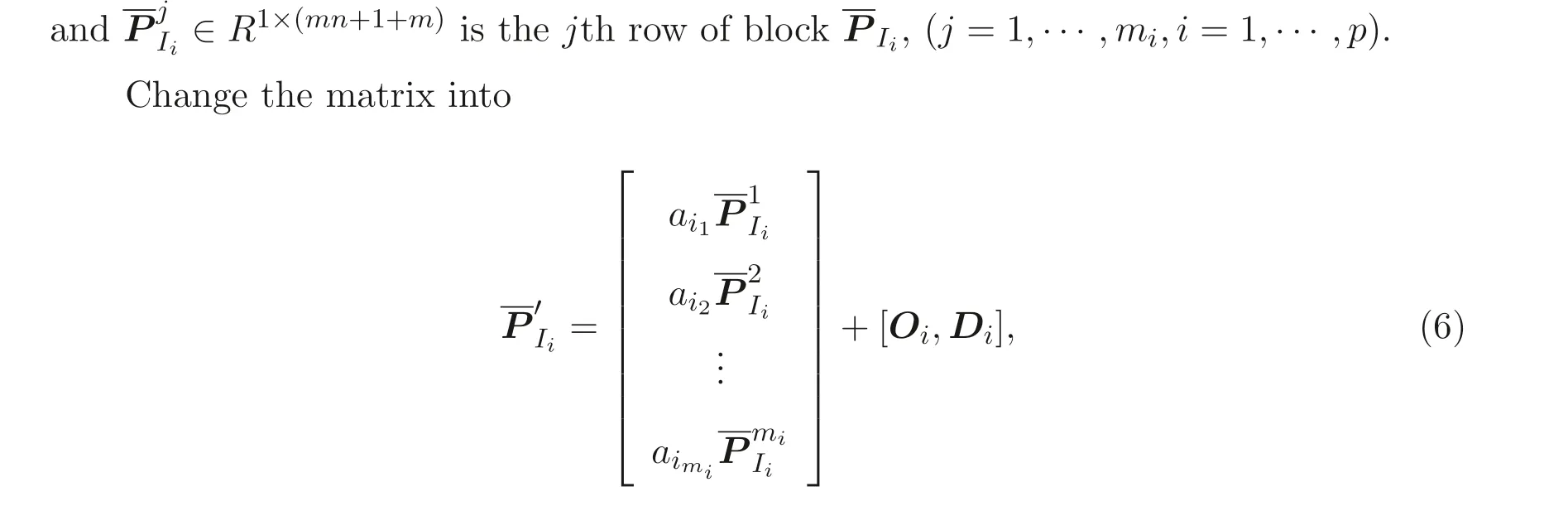
whereOi ∈Rmi×(mn+1)is a zero matrix and

Let

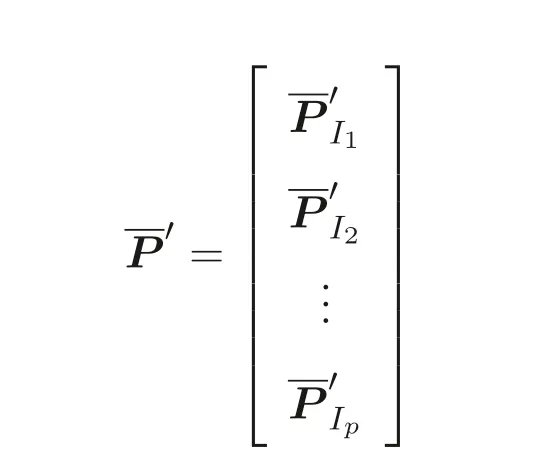
and

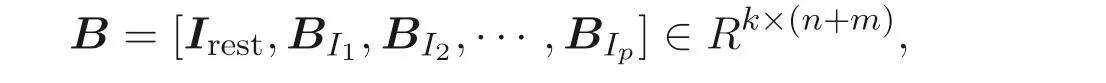
where

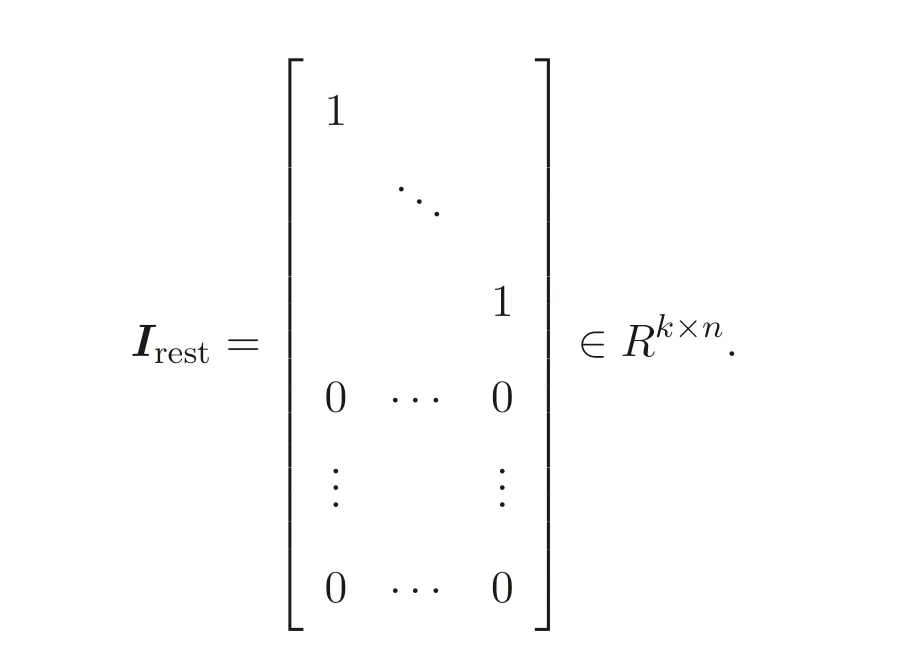
We note immediately that the rank of the randomly generated matrixB ∈Rk×(n+m)(k ≥m+n) ism+n[8]. Utilizing this fact we define the following transformations:With this transformation our program (5) turns into the following “secure” program:

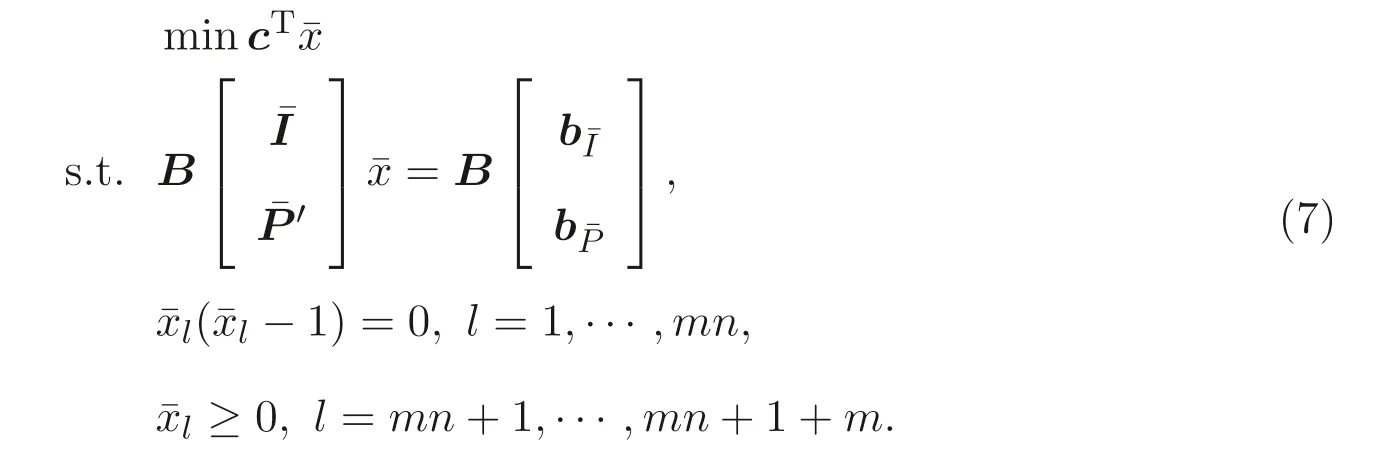
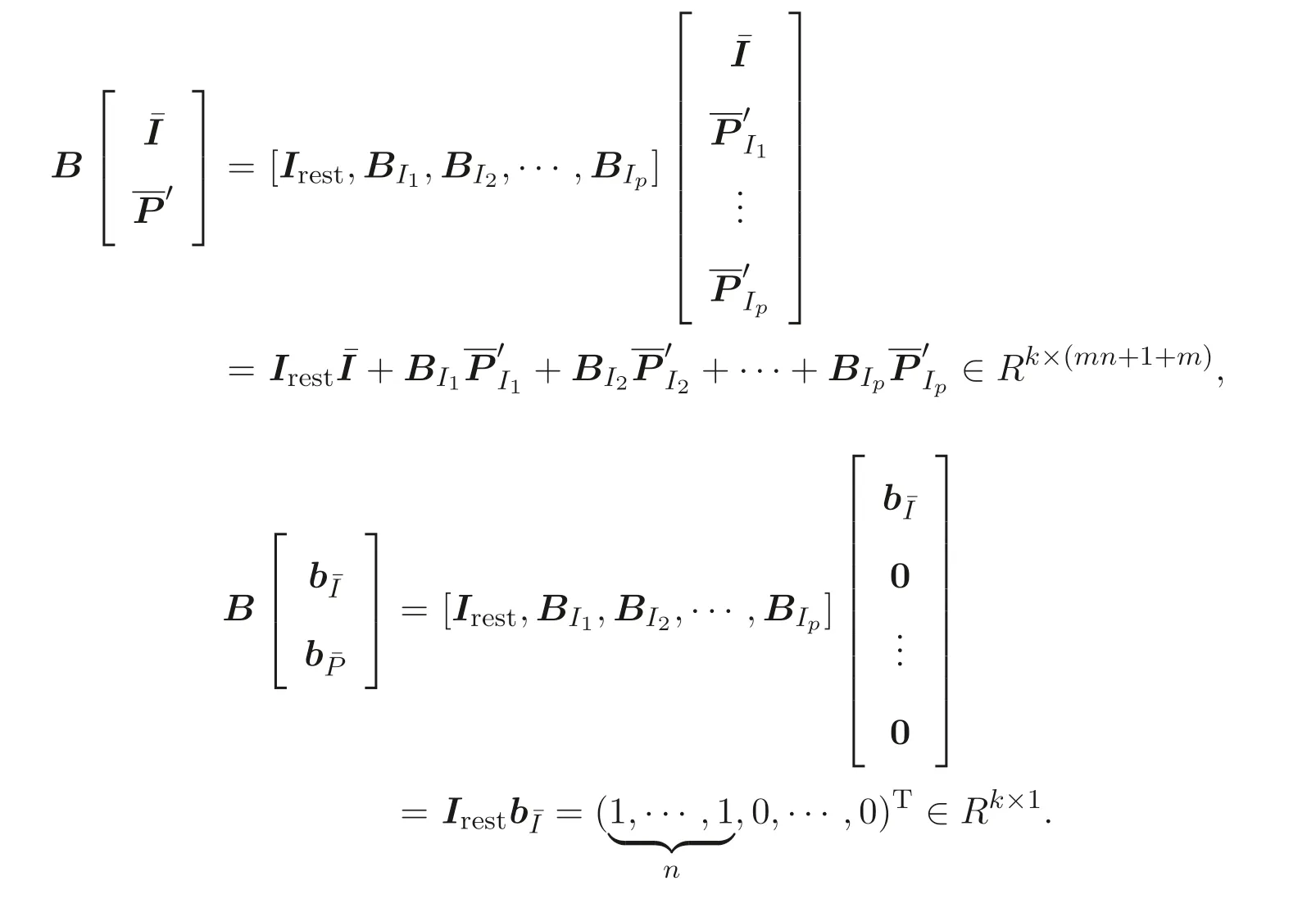
We now relate our original program (5) to the secure program (7).

Theorem 3.1Letk ≥m+nfor the random matrixB ∈Rk×(n+m). The secure program (7) is solvable if and only if the program (5) is solvable in which case the optimal objective values of the two programs are identical.

ProofBecause the rank of the random matrixBism+n, the following equivalence is obviously true

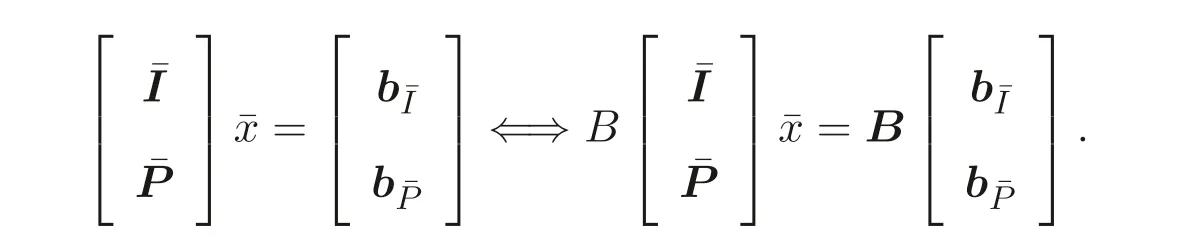
We now turn to a specific example to show the privacy-preserving process.

4 An illustrative example

In this section,a specific example is discussed to demonstrate the proposed method.

Example 4.1Consider the scheduling problemR2||Cmax: two unrelated parallel machines are available to process a set of three jobs with processing time given in a matrix

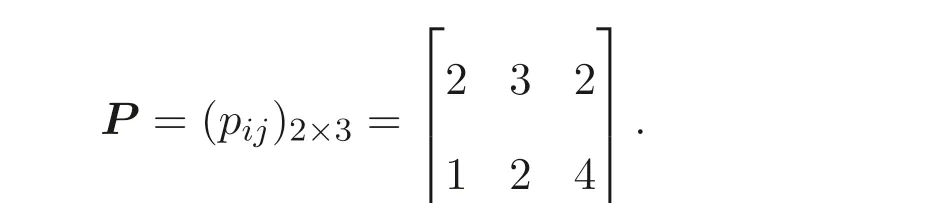
LetI1={1},I2={2}. The specific matrices and vectors corresponding to program(5) of the scheduling problem are

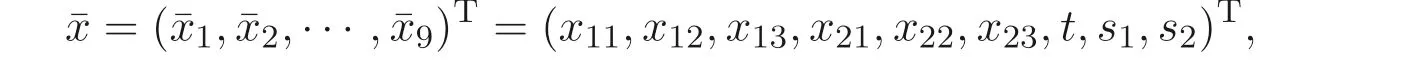
wherex11,x12,x13,x21,x22,x23are 0-1 variables andt,s1,s2are non-negative variables.

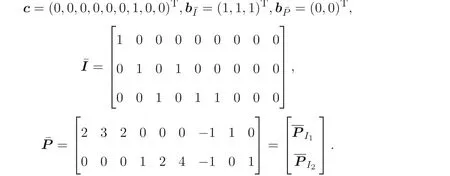
It can be shown that the optimal solution of this scheduling problem is

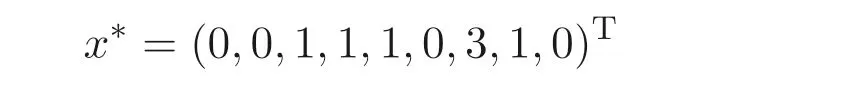
and the optimal objective value is 3, i.e., job 3 should be processed on machine 1 and job 1 and job 2 should be processed on machine 2,the makespan of the whole scheduling is 3.

Setk=5. The entity 1 generates its own privately held matrix

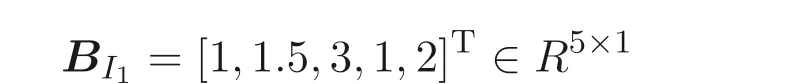
and random numbersr11=5, a11=2, and makes public only its matrix products

Also, the entity 2 generates its own privately held matrix

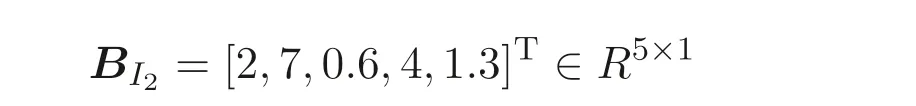
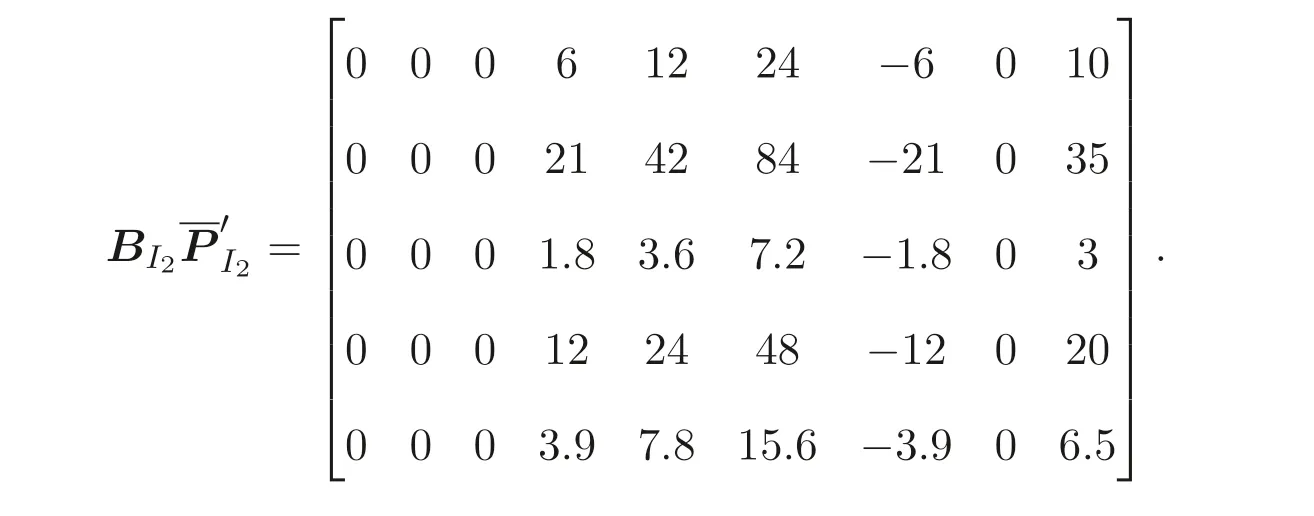
and random numbersr21=3, a21=2, and makes public only its matrix products

5 Conclusions

In this paper, we have shown how to securely model the scheduling problemRm||Cmaxwhen its processing information is horizontally partitioned among entities unwilling to share their data or make it public. The model integrates the public and the privacy-preserving data of the scheduling problem. An example illustrating the model has been given to demonstrate the utility of the model and the method to retrieve the optimal solution of the model. It would be interesting to extend this idea to other scheduling problems.