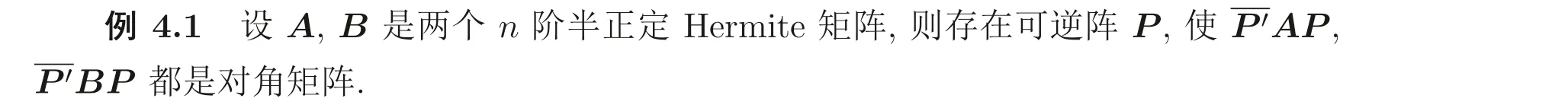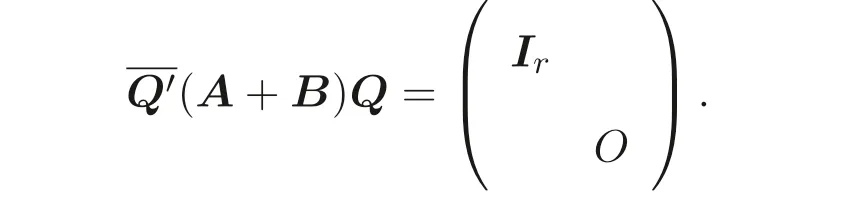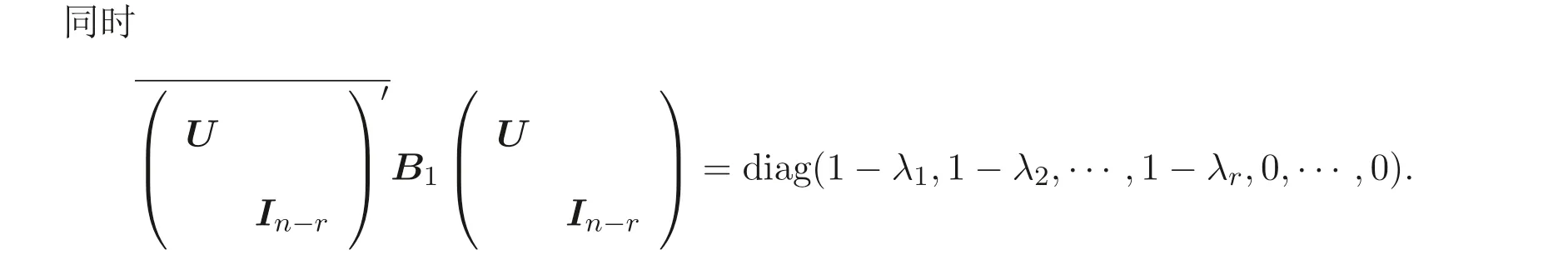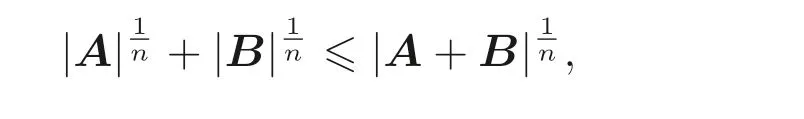關(guān)于正定矩陣的Sz′asz 不等式和Hadamard 不等式的注記
劉合國(guó), 高睿, 徐行忠, 廖軍
(湖北大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)學(xué)院, 湖北 武漢 430062)
1 引言
本文涉及的矩陣不等式見(jiàn)文獻(xiàn)[1-2], 算術(shù)- 幾何平均不等式(也稱(chēng)AM-GM 不等式) 見(jiàn)文獻(xiàn)[3], 涉及的矩陣論知識(shí)見(jiàn)文獻(xiàn)[4].
1893 年, Hadamard 證明了下面的定理, 它應(yīng)該是行列式不等式里最有名的結(jié)果之一.
Hadamard 不等式設(shè)H=(aij)n×n是復(fù)數(shù)域上的n階矩陣, 則
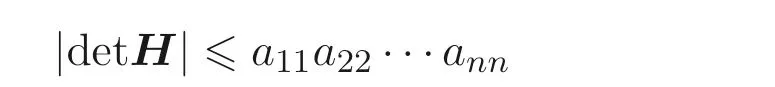
中“=” 成立當(dāng)且僅當(dāng)H是對(duì)角矩陣.
明顯的, 上述不等式等價(jià)于下面的定理:
設(shè)A=(aij)n×n是正定Hermite 矩陣, 則中“=” 成立當(dāng)且僅當(dāng)A是對(duì)角矩陣.

人們常常把這個(gè)關(guān)于正定矩陣的不等式稱(chēng)為Hadamard 不等式, 例如文獻(xiàn)[1-2]. 隨后, Sz′asz 推廣了Hadamard 不等式, 得到了一個(gè)加細(xì)的不等式, 見(jiàn)文獻(xiàn)[1-2,4].
Sz′asz 不等式設(shè)A= (aij)n×n是非對(duì)角的正定Hermite 矩陣,Pk表示A的所有k級(jí)主子式的乘積(1 ≤k≤n), 則
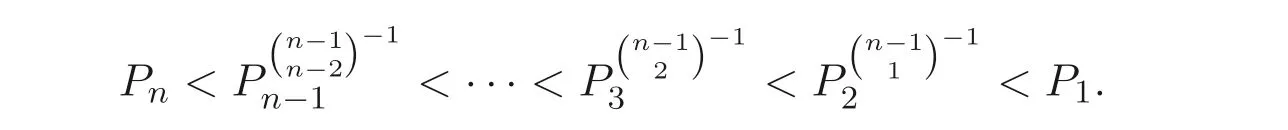
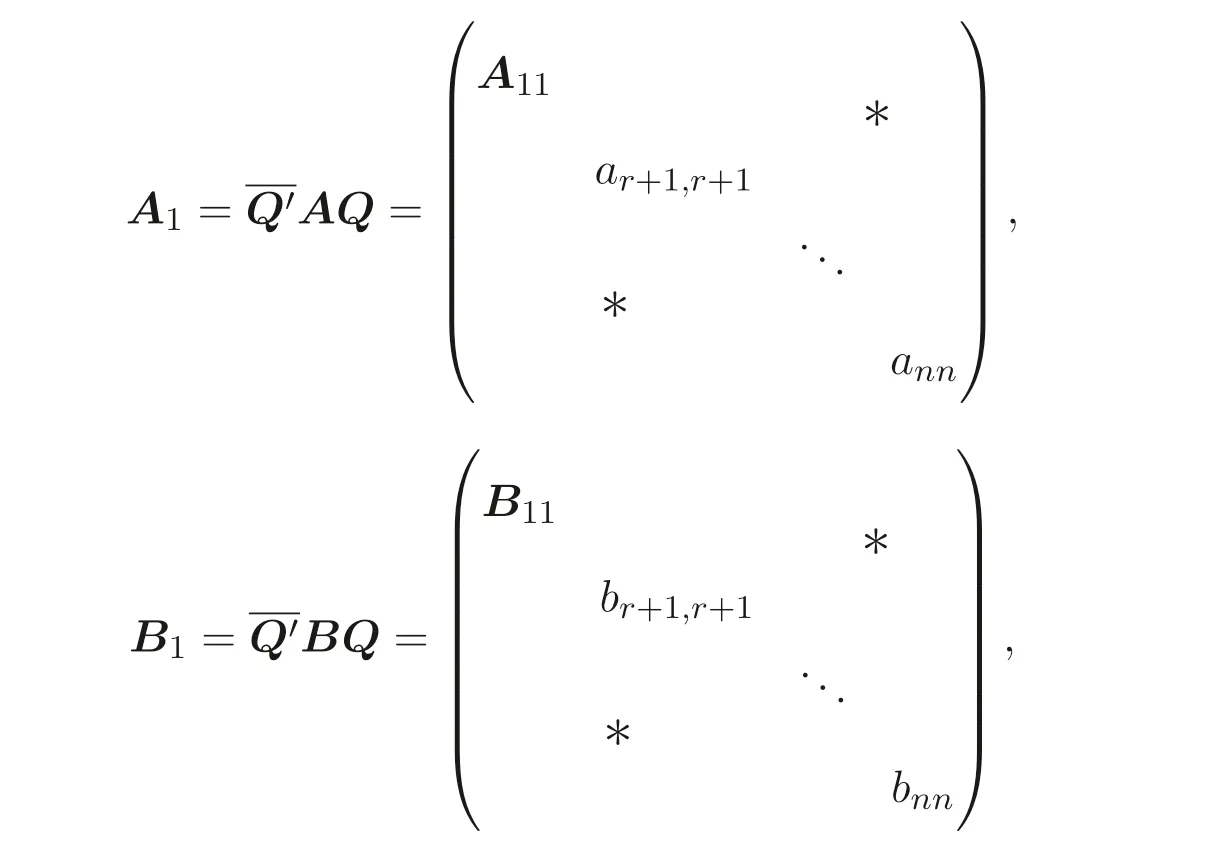
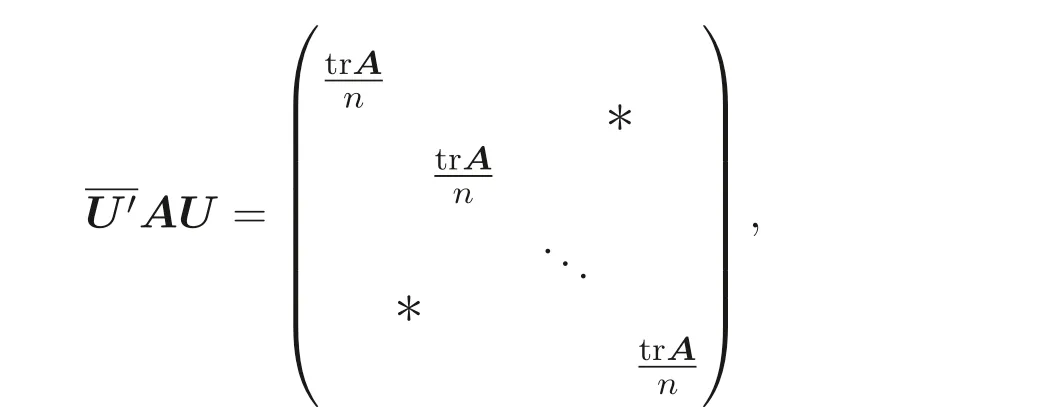
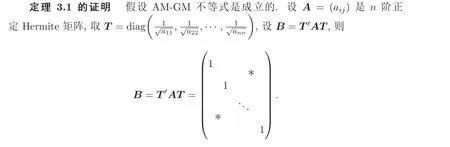
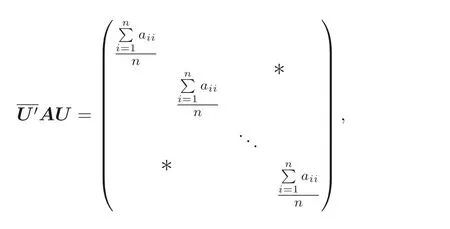
顯然, Sz′asz 不等式里“Pn 本文包括兩方面的內(nèi)容, 它們?cè)谛问缴峡词窍嗷オ?dú)立的, 但在本質(zhì)上是一脈相承的.其一, 給出Sz′asz 不等式的加法形式; 其二, 證明Hadamard 不等式等價(jià)于AM-GM 不等式. 貫穿全文的基本思想是“平均”. 有關(guān)Sz′asz 不等式的研究請(qǐng)參見(jiàn)文獻(xiàn)[6-11], 關(guān)于Hadamard 不等式和平均值不等式可參見(jiàn)文獻(xiàn)[12-15]. 這個(gè)定理的證明依賴(lài)于兩個(gè)已有的事實(shí). 引理2.1把A= (aij)n×n的所有k級(jí)主子式之和記為Qk, 1 ≤k≤n, 則A的特征多項(xiàng)式 下面用微積分的技術(shù)給出該引理的一個(gè)簡(jiǎn)潔證明. 證明對(duì)n進(jìn)行歸納. 當(dāng)n= 1,2 時(shí), 結(jié)論是易見(jiàn)的. 歸納地假設(shè)n ?1 時(shí)結(jié)論成立, 注意到ΔA(λ) 的導(dǎo)數(shù) 的展開(kāi)式的λn?k?1的系數(shù)里出現(xiàn)n ?k次, 于是 令λ=0, 可得C=(?1)nQn, 因此 引理得證. 引理2.2(Newton-Maclaurin 不等式) 設(shè)λ1,λ2,··· ,λn是n個(gè)正數(shù),σk是λ1,λ2,··· ,λn上的第k次初等對(duì)稱(chēng)函數(shù), 1 ≤k≤n, 則有 并且上式里任意一個(gè)等號(hào)成立當(dāng)且僅當(dāng)λ1=λ2=···=λn. 這不是一個(gè)平凡的結(jié)論, 證明它需要有關(guān)“對(duì)稱(chēng)和” 形式的不等式的深刻技巧, 見(jiàn)文獻(xiàn)[3] 中Problem 12.1. 有了這兩個(gè)引理, 證明定理2.1 就是常規(guī)的工作了. 定理2.1 的證明設(shè)A的特征值為λ1,λ2,··· ,λn, 從條件知λ1,λ2,··· ,λn是n 個(gè)不全相等的正數(shù). 于是A的特征多項(xiàng)式 又根據(jù)引理2.1 知, ΔA(λ)=λn ?Q1λn?1+Q2λn?2?···+(?1)n?1Qn?1λ+(?1)nQn,比較系數(shù)可知, 對(duì)每個(gè)1 ≤i≤n,Qi=σi, 進(jìn)而據(jù)引理2.2 得到 透過(guò)上面的推理, 定理2.1 完全依賴(lài)于Newton-Maclaurin 不等式這個(gè)深刻的工具,這樣定理2.1 不是平凡的結(jié)果. 沒(méi)有找到定理2.1 的脫離Newton-Maclaurin 不等式的證明, 這與Sz′asz 不等式具有本質(zhì)的不同, Sz′asz 不等式是有非常初等的證明的, 見(jiàn)文獻(xiàn)[5]. 這里B跑遍行列式為1 的正定Hermite 矩陣. 從情理上說(shuō), 定理2.1 應(yīng)該是已知的結(jié)果, 但沒(méi)有在已有的出版物上見(jiàn)到. 本文作者曾求教于矩陣論專(zhuān)家, 他們聲稱(chēng)也沒(méi)有見(jiàn)到定理2.1 這樣的結(jié)論. AM-GM 不等式是不等式理論里最重要的柱石之一, 存在許多令人嘆為觀(guān)止的證明和推廣. 在闡述Hadamard 不等式和Sz′asz 不等式時(shí), 文獻(xiàn)[1] 寫(xiě)道:“Hadamard′s inequality, like the inequality connecting the arithmetic mean and the geometric mean,caught the fancy of mathematicians, with the result that there are a wide range of different proofs and numerous extensions of this result.” 現(xiàn)在, 要證明Hadamard 不等式與AM-GM 不等式的等價(jià)性, 這個(gè)結(jié)論為文獻(xiàn)[1]的這段文字提供了一個(gè)直接的, 有力的注解. 定理3.1Hadamard 不等式與AM-GM 不等式是等價(jià)的. 在給出定理3.1 的證明之前, 先證明下面的引理. 引理3.1若A=(aij)n×n為n階Hermite 矩陣, 則存在n階酉矩陣U使得 其中trA為矩陣A的跡. 引理得證. 顯然B也是正定Hermite 矩陣, 設(shè)B的特征值為λ1,λ2,··· ,λn, 則λi>0 且 等號(hào)成立當(dāng)且僅當(dāng)B的特征值均為1, 當(dāng)且僅當(dāng)B=I, 當(dāng)且僅當(dāng) 反過(guò)來(lái), 若A=diag(a11,a22,··· ,ann) 為n階對(duì)角矩陣, 且aii>0, 則A是正定矩陣. 由引理3.1 可得, 存在n階酉矩陣U使得 由Hadamard 不等式可得 另外, 從文獻(xiàn)[1-2,4] 知, Hadamard 不等式和AM-GM 不等式都有相互獨(dú)立的證明, 定理3.1 表明它們是等價(jià)的. 已經(jīng)存在許多關(guān)于Hadamard 不等式的證明, 上節(jié)從AM-GM 不等式出發(fā)的證明應(yīng)該是早已經(jīng)存在的, 在此寫(xiě)出來(lái)是為了文章的完整性, 更是為了突出“平均” 思想的威力, 這種簡(jiǎn)單樸實(shí)的思考方式常常被忽視了. 下面再舉兩例來(lái)闡釋這種方法, 而結(jié)論也是早為人知的. 證明由于A,B是半正定矩陣, 則A+B半正定, 設(shè)r(A+B)=r, 則存在可逆矩陣Q, 使得 設(shè) 其中A11和B11是r階矩陣. 顯然A1和B1半正定, 從而對(duì)滿(mǎn)足r+1 ≤i≤n的i,有aii=bii=0. 進(jìn)一步, 由于A1是半正定Hermite 矩陣, 故可得 結(jié)論成立. 例4.2(Minkowski 不等式) 設(shè)A,B是兩個(gè)n階正定Hermite 矩陣, 則 且“=” 成立當(dāng)且僅當(dāng)存在k>0, 使得B=kA. 證明由于A,B是正定矩陣, 則A+B正定, 從而存在可逆陣P, 使得2 Sz′asz 不等式的加法形式

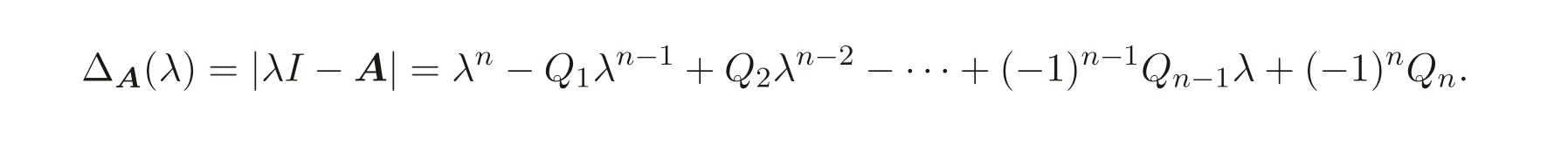

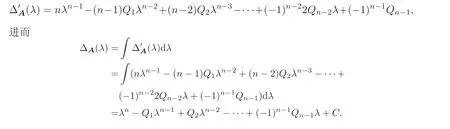
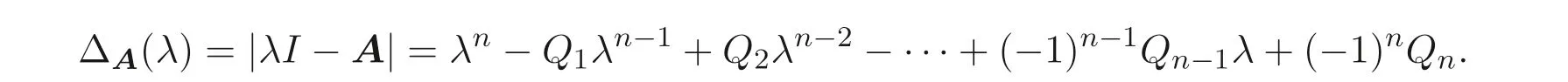
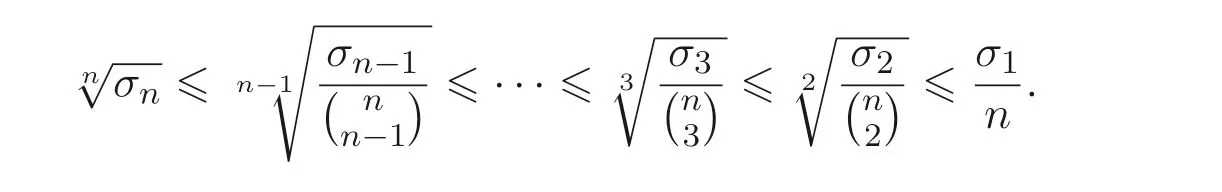
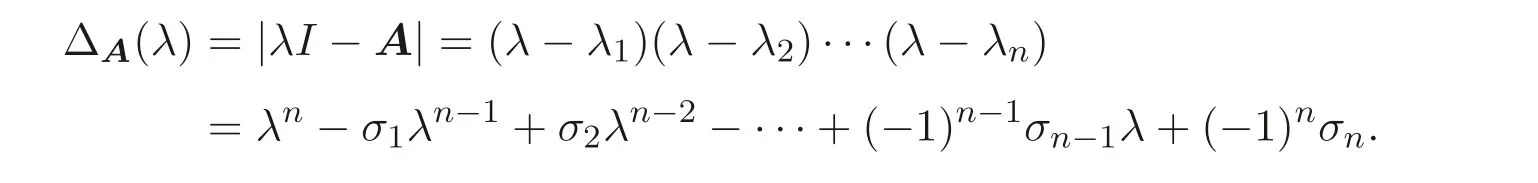
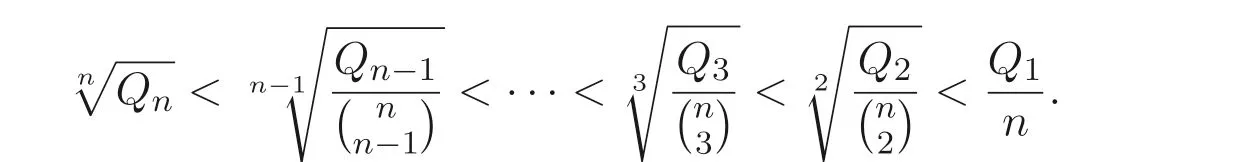

3 Hadamard 不等式與AM-GM 不等式的等價(jià)性


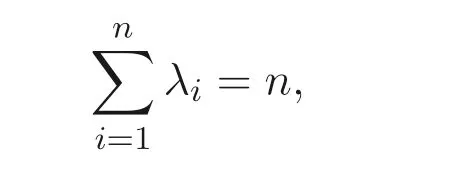
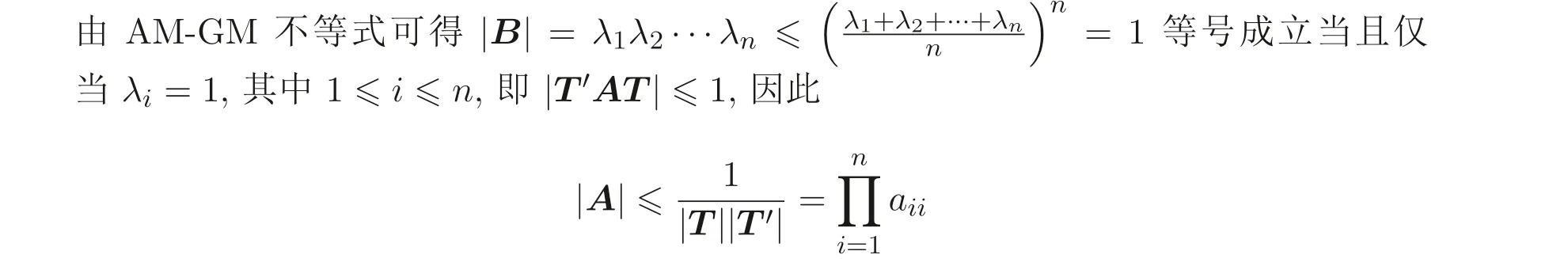
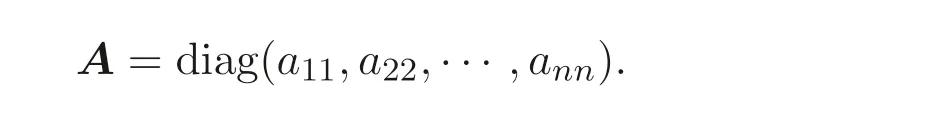
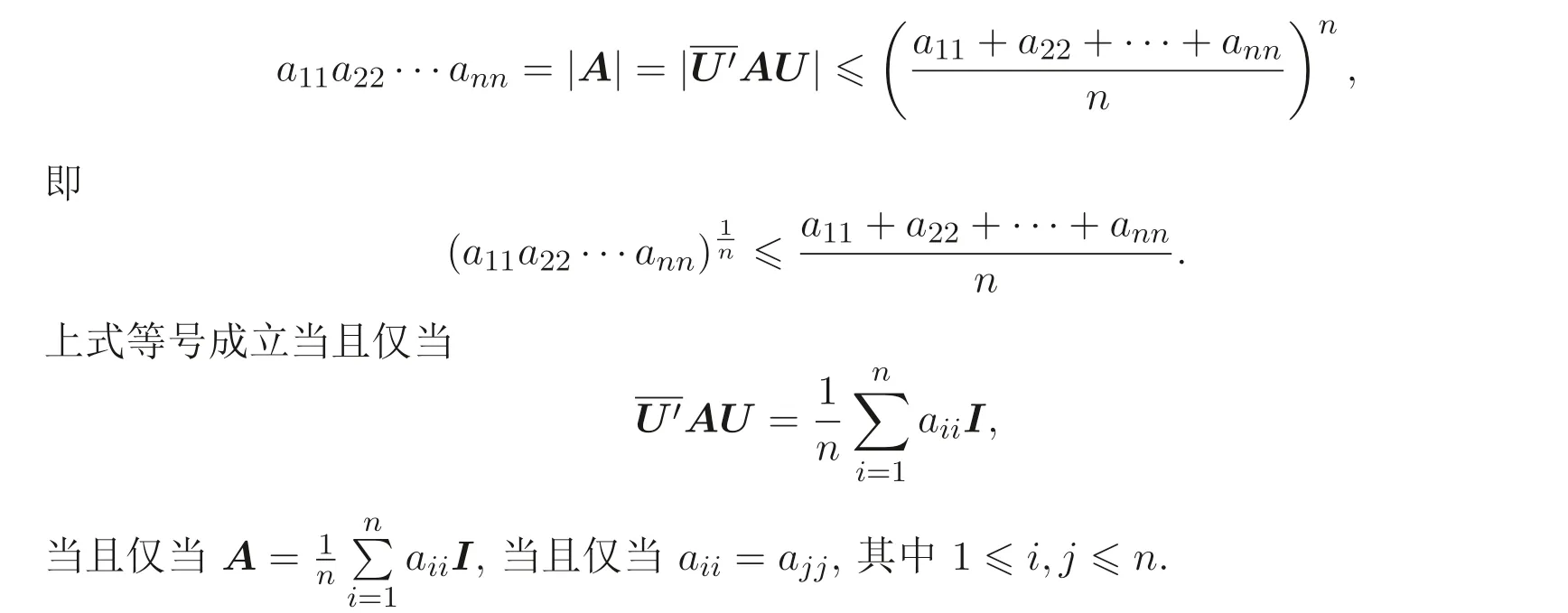
4 平均