張 艷

（閩南師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,福建漳州363000）

1 預(yù)備知識(shí)

本文考慮簡(jiǎn)單連通圖.圖G=(V(G),E(G)),這里集合V(G)是圖G的頂點(diǎn)集,集合E(G)是圖G的邊集.H和G是兩個(gè)圖,如果V(H) ?V(G)且E(H)?E(G),則稱H是G的子圖.稱不包含圈的圖為無圈圖或森林,稱連通的無圈圖為樹.用Pn表示n個(gè)頂點(diǎn)的路,Cn表示n個(gè)頂點(diǎn)的圈,Tn為n個(gè)頂點(diǎn)的樹.在完全二部圖G(X,Y)中,|X|= 1 或|Y|= 1 時(shí),稱這個(gè)圖為星圖,用Sn表示n+ 1 個(gè)頂點(diǎn)的星圖.若Vi?V,VVi表示從V中刪去Vi.以V(G)的非空子集Vi為頂點(diǎn)集,兩端點(diǎn)均在Vi中的全部邊所組成的子圖,稱G由Vi導(dǎo)出的子圖,記為G[Vi].對(duì)圖G中的2 度頂點(diǎn)依次收縮兩條與其關(guān)聯(lián)的邊稱為該2 度頂點(diǎn)的雙收縮,由圖G連續(xù)雙收縮2度頂點(diǎn)所得到的最小度至少為3的圖稱為圖G的收縮核.

圖G的匹配是指圖G的邊子集,其中任意兩條邊都不相鄰.當(dāng)匹配飽和圖中所有的頂點(diǎn),則稱為完美匹配.匹配覆蓋圖是指每一條邊都落在某個(gè)完美匹配中的連通圖.圖G的完美匹配圖,記為PM(G),是以G的每個(gè)完美匹配作為頂點(diǎn)并且兩個(gè)頂點(diǎn)相鄰當(dāng)且僅當(dāng)這兩點(diǎn)對(duì)應(yīng)于G中兩個(gè)完美匹配的對(duì)稱差恰好是一個(gè)圈而得到的圖.若PM(G)是完全圖,則稱G是完美匹配緊鄰的(perfect matching compact),簡(jiǎn)稱G是PM-緊鄰的.Wang[1]已經(jīng)證明圖G是PM-緊鄰的等價(jià)對(duì)于G中任意兩個(gè)點(diǎn)不相交的偶圈C1和C2,G-V(C1)?V(C2)沒有完美匹配.顯然K4,K6是PM-緊鄰圖.對(duì)二部完全圖Kp,q不相鄰的頂點(diǎn)之間加邊,然后用P3代替這些邊所得到的圖稱為Kp,q的外剖分.若G≠K3,3且是由將K3,3的哈密爾頓圈上的一些邊換為奇路得到的,則稱G是K3,3的H-剖分.Wang 等[1]給出點(diǎn)數(shù)大于5 的哈密頓二部圖若是PM-緊鄰的,則要么是K3,3,要么是K3,3的H-剖分的支撐哈密爾頓子圖,或者是Kp,q的外剖分,其中min{p,q}≥2.Wang[2]等已經(jīng)完全刻畫出是PM-緊鄰的無爪三正則圖.De Carvalho等[3]已經(jīng)完全刻畫出PM-緊鄰的Βirkhoff-von Neu‐mann圖.Wang[4]等已經(jīng)證明near-bipartite圖若是PM-緊鄰的當(dāng)且僅當(dāng)圖的收縮核同構(gòu)于特殊的一類圖.

圖G和圖H的笛卡兒乘積圖G×H定義為如下:V(G×H)=V(G)×V(H),E(G×H)={(u1,v1)(u2,v2)|當(dāng)u1=u2且v1v2∈E(H)或當(dāng)v1=v2且u1u2∈E(G)}.本文完全刻畫具有完美匹配的圖G和任意點(diǎn)數(shù)大于1的圖H的笛卡兒乘積圖G×H中所有具有PM-緊鄰性質(zhì)的圖.(H只有一個(gè)點(diǎn)時(shí),G×H即為G),Wang[4]等已經(jīng)完全刻畫出匹配覆蓋二部圖G是PM-緊鄰的當(dāng)且僅當(dāng)G的收縮核是K3,3或K*2.

2 主要結(jié)果

引理1[1]令G是一個(gè)有完美匹配的圖,若G是PM-緊鄰的,則下面的兩個(gè)論述是等價(jià)的:

1）對(duì)于G的任意一個(gè)偶圈C,G-V(C)最多有一個(gè)完美匹配;

2）對(duì)于G的任意兩個(gè)不交的偶圈C1和C2,G-V(C1)-V(C2)沒有完美匹配.

引理2[5]G是PM-緊鄰圖,G1是G的含有完美匹配的子圖,若G1是G的生成子圖，或G-V(G1)有唯一的完美匹配,則G1是PM-緊鄰圖.

引理1的結(jié)論等價(jià)于若G中存在兩個(gè)點(diǎn)不相交的偶圈C1和C2,使G-V(C1)-V(C2)有完美匹配,則G不是PM-緊鄰的.引理2表明若G存在一個(gè)生成子圖G1不是PM-緊鄰的,則G也不是PM-緊鄰的.

下面給出本文的主要結(jié)果.

定理1設(shè)G是一個(gè)有完美匹配的圖,H是任意點(diǎn)數(shù)大于1 的圖.若G×H是PM-緊鄰圖,則G×H是P2×P2,P2×P3,P2×C3或P2×Sn.

定理1 是下面4 個(gè)引理的自然推廣.為了完成定理1 的證明,只需要證明下面4 個(gè)引理.為了方便討論,下面用G表示有完美匹配的圖,用H表示任意點(diǎn)數(shù)大于1 的圖,這里分別考慮H是路,圈, 最大度大于2的樹及不是樹或圈的連通圖的情況.記|V(G)|=m,|V(H)|=n,這里m,n≥2.

引理3若G是一個(gè)有完美匹配的圖且G×Pn是PM-緊鄰的,則G是P2且n= 2或n= 3.

證明我們將G分為是有完美匹配的路,圈,最大度大于2的樹及不是樹或圈的連通圖這4種情形,來完成對(duì)引理3的證明.

情形1.1當(dāng)G=Pm時(shí),其中m是偶數(shù).

顯然P2×P2,P2×P3是PM-緊鄰的.下面考慮m≥4時(shí).

當(dāng)m≥4 時(shí), 記Pm×Pn上的點(diǎn)為vij, 此時(shí)1 ≤i≤m,1 ≤j≤n,如圖1. 在Pm×Pn中存在兩個(gè)偶圈C1=v11v12v22v21v11及C2=v31v32v42v41v31,且有完美匹配{v51v61,…,v(m-1)1vm1,v52v62,…,v(m-1)2vm2,…,v1(n-1)v2(n-1),…,v(m-1)(n-1)vm(n-1),v1nv2n,…,v(m-1)nvmn}覆蓋Pm×Pn-V(C1) -V(C2)中所有的點(diǎn), 如圖1. 因此當(dāng)m≥4 時(shí),Pm×Pn不是PM-緊鄰的.

因此,當(dāng)G=Pm時(shí),其中m是偶數(shù),若G×Pn是PM-緊鄰的,則G是P2且n= 2或n= 3.

圖1 笛卡兒乘積圖Pm×Pn(m ≥4,n ≥2)Fig.1 Cartesian product graph Pm×Pn(m ≥4,n ≥2)

情形1.2當(dāng)G=Cm時(shí),其中m為偶數(shù).

結(jié)合情形1.1 知道每個(gè)Cm×Pn都存在不是PM-緊鄰的生成子圖Pm×Pn.因此,當(dāng)G=Cm時(shí),其中m為偶數(shù),則G×Pn不是PM-緊鄰的.

情形1.3當(dāng)G=Tm時(shí),這里Tm是指具有完美匹配且最大度大于2的樹.

對(duì)有完美匹配的Tm進(jìn)行頂點(diǎn)劃分(類似的劃分在引理2 的證明中也會(huì)用到).因?yàn)門m有完美匹配,則Tm中存在奇長路,使刪去路上的邊和點(diǎn)后得到的圖是一個(gè)有完美匹配的森林,從這樣的奇長路中取最長的一條并將路上所有頂點(diǎn)記為V1.同樣,在刪去最長奇長路后得到的有完美匹配的森林中也存在奇長路,使刪去路上的邊和點(diǎn)后得到的圖是一個(gè)有完美匹配的圖,再從這樣的奇長路中取最長的一條并將路上所有頂點(diǎn)記為V2. 重復(fù)操作下去得到頂點(diǎn)集V1,…,Vk,Vk+1. 此時(shí)?i,j∈{1,…,k+ 1},Vi?Vj= ?且V1?…?Vk?Vk+1=V(Tm),|V1|,…,|Vk|,|Vk+1|是單調(diào)不增的偶數(shù)且|V1|≥4.對(duì)有完美匹配的Tm的頂點(diǎn)劃分如圖2.Tm×Pn如圖3. 結(jié)合情形1.1 易知G[V1]×Pn中存在兩個(gè)點(diǎn)不相交的偶圈C1和C2, 使G[V1]×Pn-V(C1)?V(C2)上所有點(diǎn)被完美匹配覆蓋, 若還存在完美匹配覆蓋Tm×Pn-G[V1]×Pn中的點(diǎn),則Tm×Pn不是PM-緊鄰的.

記|Vt|=l(2 ≤t≤k+1),記Tm×Pn中第t個(gè)分塊G[Vt]×Pn上的頂點(diǎn)為vt ij,此時(shí)1 ≤i≤l,1 ≤j≤n.在完美匹配{vt11vt21,…,vt(l-1)1vtl1,vt12vt22,…,vt(l-1)2vtl2,vt1(n-1)vt2(n-1),…,vt(l-1)(n-1)vtl(n-1),vt1nvt2n,…,vt(l-1)nvtln}覆蓋第t個(gè)分塊上所有頂點(diǎn),如圖4.即存在完美匹配覆蓋Tm×Pn-G[V1]×Pn中的點(diǎn).因此Tm×Pn不是PM-緊鄰的.

因此,當(dāng)G=Tm時(shí),這里Tm是指具有完美匹配且最大度大于2的樹,則G×Pn不是PM-緊鄰的.

情形1.4當(dāng)G是有完美匹配的不是樹或圈的連通圖.

結(jié)合情形1.2 知道每個(gè)G×Pn都存在不是PM-緊鄰的生成子圖Tm×Pn.因此,當(dāng)G是指有完美匹配的不是樹或圈的連通圖,則G×Pn不是PM-緊鄰的.

引理1得證.

由于每個(gè)G×Cn都存在生成子圖G×Pn,結(jié)合定理1 知道G×Cn中除了P2×C3都不是PM-緊鄰的,而P2×C3顯然是PM-緊鄰的.得出下面的推論.

引理4若G是一個(gè)有完美匹配的圖且G×Cn是PM-緊鄰的,則G是P2且n= 3.

圖2 含有完美匹配的Tm(m ≥4)的頂點(diǎn)劃分Fig.2 Vertex partition of Tm(m ≥4)with perfect matchings

圖3 笛卡兒乘積圖Tm×Pn(m ≥4,n ≥2)Fig.3 Cartesian product graph Tm×Pn(m ≥4,n ≥2)

圖4 笛卡兒乘積圖G[Vt]×PnFig.4 Cartesian product graph G[Vt]×Pn

引理5若G是一個(gè)有完美匹配的圖,Tn是最大度大于2 的樹且G×Tn是PM-緊鄰的, 則G是P2且Tn=Sn.

證明我們將G分為有完美匹配的路,圈,最大度大于2的樹及不是樹或圈的連通圖這4種情形,來完成對(duì)引理的證明.

情形2.1當(dāng)G=Pm時(shí),其中m為偶數(shù).

當(dāng)m≥4 時(shí), 類似情形1.2 對(duì)Tn的頂點(diǎn)劃分, 此時(shí)?i,j∈{1,…,k+ 1},Vi?Vj= ?且V1?…?Vk?Vk+1=V(Tn),|V1|,…,|Vk|,|Vk+1|單調(diào)不增并且|V1|≥3. 對(duì)Tn的頂點(diǎn)劃分如圖5. 根據(jù)情形1.1知道Pm×G[V1]不是PM-緊鄰的.若還存在完美匹配覆蓋Pm×Tn-Pm×G[V1]上的點(diǎn),則Pm×Tn不是PM-緊鄰的. 記|Vt|=l(2 ≤t≤k+ 1), 記Pm×Tn上第t個(gè)分塊Pm×G[Vt]上的頂點(diǎn)為vt ij, 此時(shí)1 ≤i≤m,1 ≤j≤l. 存在完美匹配{vt11vt21,…,vt(m-1)1vtm1,vt12vt22,…,vt(m-1)2vtm2,…,vt1lvt2l,…,vt(m-1)lvtml}覆蓋第t個(gè)分塊上所有頂點(diǎn),如圖6,即能找到完美匹配覆蓋Pm×Tn-Pm×G[V1]中的點(diǎn).因此當(dāng)m≥4 時(shí),Pm×Tn不是PM-緊鄰的.

接下來只用考慮當(dāng)m= 2的情況.

當(dāng)Tn=Sn時(shí),P2×Sn中任意兩個(gè)偶圈至少有兩個(gè)公共頂點(diǎn),即P2×Sn是PM-緊鄰的;當(dāng)Tn≠Sn時(shí),類似于上面情形1.2的證明,容易證明P2×Tn不是PM-緊鄰的.

因此,當(dāng)G=Pm時(shí),其中m為偶數(shù),且G×Tn是PM-緊鄰的,則G是P2且Tn=Sn.

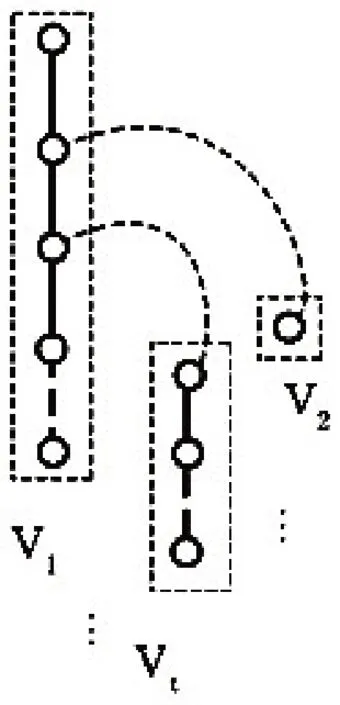
圖5 Tn 的頂點(diǎn)劃分Fig.5 Vertex partition of Tn

圖6 笛卡兒乘積圖Pm×G[Vt]Fig.6 Cartesian product graph Pm×G[Vt]

情形2.2當(dāng)G=Cm時(shí),其中m為偶數(shù).

由情形2.1知道每一個(gè)Cm×Tn都存在一個(gè)不是PM-緊鄰的生成子圖Pm×Tn.

因此,當(dāng)G=Cm時(shí),這里m為偶數(shù),則圖G×Tn不是PM-緊鄰的.

情形2.3當(dāng)G=Tm時(shí),這里Tm是指有完美匹配且最大度大于2的樹.

類似情形1.2 對(duì)Tm的頂點(diǎn)劃分,此時(shí)|V1|,…,|Vk|,|Vk +1|是單調(diào)不增的偶數(shù)且|V1|≥4.根據(jù)情形1.1 易知G[V1]×Tn不是PM-緊鄰的,且存在完美匹配覆蓋G×Tn上分塊G[Vt]×Tn(2 ≤t≤k+1)上的頂點(diǎn).

因此,當(dāng)G=Tm時(shí),這里Tm是指有完美匹配且最大度大于2的樹,則G×Tn不是PM-緊鄰的.

情形2.4當(dāng)G是有完美匹配的不是樹或圈的連通圖.

由情形2.2知道每一個(gè)G×Tn都存在一個(gè)不是PM-緊鄰的生成子圖Tm×Tn.

因此,當(dāng)G是有完美匹配的不是樹或圈的連通圖,則G×Tn不是PM-緊鄰的.

引理2得證.

接下來討論H為不是樹或圈的連通圖.每個(gè)G×H都存在生成子圖G×Tn,且由定理2知G×Tn中除了P2×Sn都不是PM-緊鄰的,則G×H中除了P2×H外(此時(shí)H存在Sn作為生成子圖)都不是PM-緊鄰的.這就引出下面結(jié)論.

引理6若G是一個(gè)有完美匹配的圖，H為不是樹或圈的連通圖,則G×H不是PM-緊鄰的.

證明現(xiàn)在只需證明P2×H(此時(shí)H存在Sn作為生成子圖)不是PM-緊鄰的. 記Sn的頂點(diǎn)為{v0,v1,v2,…,vn},對(duì)H的頂點(diǎn)進(jìn)行排序,使v1v2∈E(H).記P2×H上的頂點(diǎn)為vij(此時(shí)0 ≤i≤n,j= 1,2),如圖7. 在P2×H中存在C1=v01v02v32v31v01,C2=v11v12v22v21v11且有完美匹配{v41v42,…,vn1vn2}覆蓋P2×H-V(C1)-V(C2)上的頂點(diǎn),如圖8.因此P2×H(H存在Sn作為生成子圖)不是PM-緊鄰的.

圖7 圖HFig.7 graph H

圖8 笛卡兒乘積圖P2×HFig.8 Cartesian product graphP2 ×H

故推論2得證.