具有Beddington-DeAngelis發(fā)生率和雙流行病的隨機SIQS流行病模型的動力學(xué)研究
呂 杰, 韋煜明, 彭華勤
(廣西師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院,廣西 桂林 541006)
眾所周知,全球每天都有數(shù)萬人因疾病而失去生命,死亡率高的疾病會影響人的平均壽命,同時也會削弱國家的經(jīng)濟實力. 為了有效預(yù)防和控制,越來越多的數(shù)學(xué)家提出用數(shù)學(xué)模型來研究傳染病的動力學(xué)行為,并在生物學(xué)中得到了廣泛應(yīng)用[1—3]. 在疾病發(fā)生時,為了減少受感染人數(shù),政府或組織通常會采取隔離措施. 此時所用生物數(shù)學(xué)模型稱為SIQS流行病模型[4]:
其中:S表示易感人群數(shù)量;I表示受感染但未被隔離人群數(shù)量;Q表示受感染后被隔離人群數(shù)量;Λ為新進人口數(shù)量;μ表示自然死亡率;γ,ε分別表示受感染個體和被隔離個體的恢復(fù)率;α表示因病死亡率;β表示接觸率;δ表示已受感染個體的隔離率.

其中:I1,I2表示被A病毒和B病毒感染的數(shù)量;β1,β2分別為2種疾病的接觸率;α1,α2分別為2種疾病的因病死亡率;γ1,γ2分別為2種疾病的恢復(fù)率;ai,bi(i=1,2)為抑制效果參數(shù).
基于以上模型分析,本文提出新的具有Beddington-DeAngelis發(fā)生率的雙流行病SIQS模型
(1)

本文將討論隨機擾動強度對模型(2)的影響,確定隨機系統(tǒng)的兩種疾病滅絕和持久的閾值.
1 全局正解的存在性和唯一性
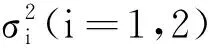





P{τ∞≤T}>ε.
因此,存在一個正整數(shù)k1>k0, 使得
P{τ∞≤T}≥ε,?k≥k1.

V(S,I1,I2,Q)=
(S-1-lnS)+(I1-1-lnI1)+
(I2-1-lnI2)+(Q-1-lnQ).
顯然,函數(shù)V非負(fù),對?k>k0,T>0, 對V函數(shù)應(yīng)用It公式,可得
dV(S,I1,I2,Q)=LV(S,I1,I2,Q)dt+

LV(S,I1,I2,Q)=



δ1I1+δ2I2+(μ+α3+ε)-(μ+α3+ε)Q≤
其中K為正整數(shù),則有
(3)
對(3)式兩邊同時從0到τk∧T=min{τk,T}積分,并求期望
即
E(V(S(τk∧T)),I1(τk∧T),
I2(τk∧T),Q(τk∧T)))≤
E(V(S(0),I1(0),I2(0),Q(0))+KE(τk∧T)≤
E(V(S(0),I1(0),I2(0),Q(0))+KT.
(4)

V(S(τk∧T)),I1(τk∧T),I2(τk∧T),
Q(τk∧T))≥
由(4)式可得
V(S(0),I1(0),I2(0),Q(0))+KT≥
E(IΩk(ω)V(S(τk∧T),I1(τk∧T),
I2(τk∧T),Q(τk∧T)))≥
其中IΩk(ω)是示性函數(shù),當(dāng)k→∞時,
∞>V(S(0),I1(0),I2(0),Q(0))+KT=∞,
矛盾,故有τ∞=∞, 得證,即存在全局唯一正解.
2 疾病的滅絕性

則系統(tǒng)(2)的兩種流行病都將滅絕.a.s.
證明對系統(tǒng)(2)應(yīng)用It公式可得
(5)
兩邊同時求積分并除以t可得

(6)

定義

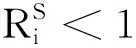
證明由模型(2)易得d(S+I1+I2+Q)≤(Λ-μ(S+I1+I2+Q))dt,則有


(7)
對(7)式取極限得
即2種疾病都將會消亡.
由于2種疾病將會消亡,設(shè)0 當(dāng)ε1→0,ε2→0時, (8) 又因為 (9) 由(8)式和(9)式可得 由定理2和定理3可知,相對大的噪音強度會使疾病消亡,在一定條件下相對小的白噪音強度也會使疾病消亡. 本節(jié)主要討論系統(tǒng)(2)的兩種流行病的持久性,主要包括2種情況:①一種流行病消亡的同時,另一種流行病持久;②兩種流行病都持久. 對系統(tǒng)(2)等號兩邊同時從0到t積分并除以t可得 (μ+α3+ε)Q(s))d(s)= Λ-μ〈S(t)〉-C1〈I1(t)〉-C2〈I2(t)〉≥ Λ-μ〈S(t)〉-C1〈I1(t)〉-C2ε2, (10) 由(10)式可得 (μ+α1+γ1+δ1)I1(t)dt+ σ1S(t)dB1(t). (11) 對(11)式兩邊同時從0到t積分并除以t可得 (12) 由(12)式可得 當(dāng)I1(t)≥1時, (13) 當(dāng)0 (14) 當(dāng)ε2→0時,對(13)~(14)式取極限可得 (ⅱ)的證明方法與(ⅰ)相似,證明略. (ⅲ) 由(10)式可得 定義C2-函數(shù)V: dV(t)= (15) 對(15)式兩邊從0到t積分并除以t可得 Δmax(〈I1(t)〉+〈I2(t)〉)- (16) 其中 由(16)式可得 (〈I1(t)〉+〈I2(t)〉)≥ (17) 對(17)式取極限可得 用Milstein方法[14]來驗證所得結(jié)論,并總結(jié)本文的重要結(jié)論. 首先將模型(2)離散化: Q(k+1)=Q(k)+(δ1I1(k)+δ2I2(k)- (μ+α3+ε)Q(k))Δt, 其中ξ(k),k=1,2,3,…,n是服從N(0,1)分布的獨立的隨機變量. 首先當(dāng)系統(tǒng)(2)中σ1=0,σ2=0時為SIQS確定性模型,即不受環(huán)境干擾取參數(shù)Λ=1,μ=0.1,β1=0.5,β2=0.7,γ1=0.1,γ2=0.1,δ1=0.1,δ2=0.2,α1=0.1,α2=0.2,α3=0.2,a1=1,a2=1,ε=0.1,b1=2,b2=1,確定性模型隨時間t變化的趨勢見圖1. 圖1 確定性系統(tǒng)(S,I1,I2,Q)的軌跡圖 由圖2可知,兩種疾病滅絕時,均有 圖2 隨機系統(tǒng)(S,I1,I2,Q)兩種疾病均滅絕的軌跡圖 由定理4可知: 圖3 隨機系統(tǒng)(S,I1,I2,Q)單一疾病滅絕的軌跡圖 由圖4可知,兩種疾病在此狀態(tài)下持久.3 疾病在時間均值意義下的持久性

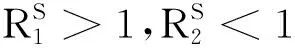


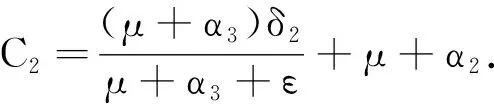







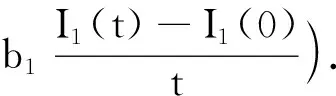




4 數(shù)值模擬
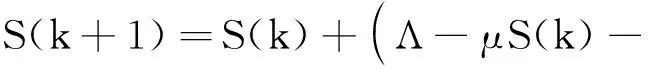

4.1 疾病的滅絕性

4.2 疾病在均值意義下的持久性
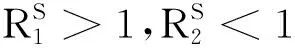



5 結(jié)論


