Xingxiao LI (李興校)? Ruina QIAO(喬瑞娜) Yangyang LIU (劉洋洋)

School of Mathematics and Information Sciences, Henan Normal University, Xinxiang 453007, China E-mail : xxl@henannu.edu.cn; 1540007578@qq.com; 820915350@qq.com

Note that,different from what is used in[2],the translating vectorTin the present article does not need to be time-like.

Recently,L′opez classified in[13]allλ-translators in R3that are invariant by a group of translations(cylindrical surfaces)and a group of rotations(surfaces of revolution).He also studied in[14]the shape of a compactλ-translator of R3in terms of the geometry of its boundary,obtaining some necessary conditions for the existence of two-dimensional compactλ-translators with a given closed boundary curve.In particular,he proved that there do not exist any closed(that is,compact without boundary)λ-translators of dimension two.

On the other hand,just asλ-translating solitons are generalizations of the translators of mean curvature flow,theλ-hypersurfaces defined by Cheng and Wei in[6]are generalizations of the hypersurface self-shrinkers of mean curvature flow.Note that these kinds of self-shrinkers also sit well in the singularity theory of the mean curvature flow,corresponding to the limit flow by a proper blow-up procedure near type I singular points([10,11]).As is known,there have been many rigidity theorems and classification theorems for self-shrinkers in Euclidean space and in pseudo-Euclidean space.Also,some nice properties of the Lagrangian angle and the K¨ahler angle of immersed surfaces are discussed in[12].Furthermore,there have been several interesting and important results in the study ofλ-hypersurfaces.In particular,Cheng and Wei recently obtained a classification theorem using their own generalized maximum principle([4])specially forλ-hypersurfaces,which generalizes an interesting classification theorem in[3]for self-shrinkers.

Theorem 1.1([5])Letx:M2→R3be a completeλ-surface in R3with the second fundamental form of a constant square norm.Then either

2 Preliminaries

and the(non-normalized)mean curvatureHof the hypersurfacexis defined byH=hii.Moreover,the square norm of the second fundamental formhis given byS=.Clearly,at any pointp∈Mm,

with the equality holding if and only ifpis an umbilical point where the principal curvaturesλ1,···,λmare all equal.

Theorem 2.1([2])Let(Mm,g)be a complete Riemannian manifold,andVaC1vector field onMm.Suppose that RicV≥?F(r)g,whereris the distance function onMmfrom a fixed point,andF:R→R is a positive continuous function satisfying that

From now on,and when no confusion can occur,we always omit the notationsx?andx?.

3 Proof of the Main Results

The main idea of Cheng and Wei in[5]will be partially used in this section.We shall first consider the space-likeλ-translators in the Minkovski space.For this,we shall always takeε=?1 for the formulas that appeared in Section 2.

Case(1)ˉΦ>0.Then there must be a subsequence P1?P such thatΦ(pk)>0 for eachpk∈P1.Denotep=pkfor an arbitrarily givenpk∈P1,and letλ1<λ2be the principal curvatures ofxnear the given pointp.Then it is easily seen that,unique up to a minus sign,there exists some oriented orthonormal frame field{e1,e2}nearpsuch thathij=λiδijfori,j=1,2.It is clear that,when the frame{e1,e2}changes by a sign,all the components of a covariant tensorTof even order keep invariant,while all the components of a covariant tensorTof odd order will change their sign.Therefore,if

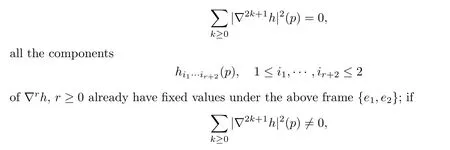
we can choosekto be the smallest number with?2k+1h(p)0,and thus the frame field{e1,e2}is uniquely given by demanding that the first nonzero component of?2k+1his positive,with respect to the natural order of the set of all the components of?2k+1h.Thus,all the components of?rh(r≥0)are also fixed.

Case(2)There is a subsequence P1?P,consisting of only umbilical points.Then we haveλ1(pk)=λ2(pk).Writep:=pk.Let{e1,e2}be an arbitrary oriented orthonormal tangent frame field aroundp.Thenhij(p)≡h(ei,ej)(p)=λi(p)δij.

Moreover,by(3.1),it holds atpthat

In particular,all the componentshi1i2···ir+2(pk)of?rh(pk),r≥0 are well-defined for eachk,giving well-defined sequences accordingly.

Case 2There are only a finite number of umbilical points in the sequence{pk}.Then we have a subsequence of{pk},still denoted by{pk},consisting of non-umbilical points.It then easily follows from Proposition 3.2(see Case(1)in the proof)that we can choose a certain basis{e1(pk),e2(pk)}such that

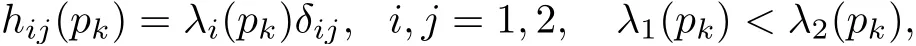
and all the componentshi1i2···ir+2(pk)of?rh(pk),r≥0 are well-defined for eachk,giving again well-defined sequences,accordingly.

To sum up,without loss of generality,we can assume that there exists a good choice of tangent frame field{e1,e2}nearpkfor eachksuch that

Proof of the second main theorem(Theorem 1.3)

A careful check tells us that Theorem 1.3 can be proved via the same argument,similar computations as to those in the proof of Theorem 1.2(takingε=1 in the relevant formulas of Section 2),and a replacement of Lemma 3.1 by the following proposition:

Proposition 3.7(cf.Lemma 3.1)Letx:M2→R3be a 2-dimensional completeλtranslator in R3with the second fundamental formhof constant square normS.IfS>0,then infH2>0.

ProofChoose a sequence{pk}onM2such that

By using the argument in the proof of Proposition 3.2 one can show that,passing to a suitable subsequence,all the sequences{hij(pk)},{hijl(pk)}and{hijlm(pk)}can be made welldefined by suitable choices of local frame fields around each pointpk,with

fork=1,2,···.The constancy ofSguarantees that they are all bounded.Thus,without loss of generality,we can also assume the existence of the limits of these sequences and use a bar to denote the corresponding limits.For example,