ON APPROXIMATE EFFICIENCY FOR NONSMOOTH ROBUST VECTOR OPTIMIZATION PROBLEMS?
Tadeusz ANTCZAK
Faculty of Mathematics and Computer Science, University of Lód′z, Banacha 22, 90-238 Lódz, Poland E-mail: tadeusz.antczak@wmii.uni.lodz.pl
Yogendra PANDEY
Department of Mathematics, Satish Chandra College, Ballia 277001, India
Vinay SINGH
Department of Mathematics, National Institute of Technology, Aizawl-796012, Mizoram, India
Shashi Kant MISHRA
Department of Mathematics, Banaras Hindu University, Varanasi-221005, India
Abstract In this article,we use the robust optimization approach(also called the worst-case approach) for finding ?-efficient solutions of the robust multiobjective optimization problem defined as a robust (worst-case) counterpart for the considered nonsmooth multiobjective programming problem with the uncertainty in both the objective and constraint functions.Namely, we establish both necessary and sufficient optimality conditions for a feasible solution to be an ?-efficient solution (an approximate efficient solution) of the considered robust multiobjective optimization problem. We also use a scalarizing method in proving these optimality conditions.
Key words Robust optimization approach; robust multiobjective optimization; ?-efficient solution; ?-optimality conditions; scalarization
1 Introduction
Robust optimization methodology (the worst-case approach) is a powerful approach for examining and solving optimization problems under data uncertainty. In robust optimization,the data is uncertain but bounded, that is, the data is varying in a given uncertainty set,and we choose the best solution among the robust feasible ones; for detail, we refer to [1–6,9, 12, 20–26, 28, 29, 31, 32, 38]. Ben-Tal et al. [5] introduced the concept of the uncertain linear optimization problem and its robust counterpart, and discussed the computational issues. Also, Bertsimas et al. [6] characterized the robust counterpart of a linear mathematical programming problem with uncertainty set described by an arbitrary norm. Jeyakumar and Li[23, 24] presented basic theory and applications of an uncertain linear mathematical program problem. Jeyakumar and Li [25] derived a robust theorem of the alternative for parameterized convex inequality systems using conjugate analysis and introduced duality theory for convex mathematical programming problems in the face of data uncertainty via robust optimization.Jeyakumar et al. [26] considered a nonlinear optimization problem with face of data uncertainty and established robust KKT necessary and sufficient optimality conditions for a robust minimizer. Furthermore, Jeyakumar et al. [26] introduced robust duality theory for generalized convex mathematical programming problems in the face of data uncertainty within the framework of robust optimization and established robust strong duality between an uncertain nonlinear primal optimization problem and its uncertain Lagrangian dual.
Robust optimization for solving multiobjective optimization problems with uncertain data is a current topic of research. Kuroiwa and Lee [31] defined three kind of robust efficient solutions and established necessary optimality theorems for weakly and properly robust efficient solutions for the considered uncertain multiobjective optimization problem. Recently, Chuong[9]established the necessary optimality conditions and,under the generalized convexity assumptions, sufficient optimality conditions for a (weakly) robust efficient solution of the considered uncertain multiobjective programming problem. Besides, robust multiobjective optimization with optimality defining by a partial order has been widely applied to solve many practical problems like internet routing, portfolio optimization, energy production scheduling in microgrids, transport, agriculture, industry-specific applications, health care applications, among others (see, for example, [3, 7, 8, 10, 14–17, 27, 30]).
In recent years, many authors have established epsilon optimality conditions for several kind of optimization problems (see, for example, [13, 18, 19, 32–36, 39, 40]). Lee and Lee [32]established optimality theorems for epsilon solutions of the scalar robust convex optimization problem.
In this article, we treat the robust approach for the considered uncertain multiobjective programming problem with the uncertainty in both objective and constraint functions which is the worst case approach for finding approximate efficient solutions for such multiobjective optimization problems. In this approach, for the considered uncertain multiobjective optimization problem, its robust (worst-case) counterpart is constructed as an associated robust multiobjective optimization problem. Then, motivated by works of Kuroiwa and Lee [31] and Lee and Lee[32],we derive the ?-efficiency theorem for the considered uncertain multiobjective programming problem by examining its robust (worst-case) counterpart. In other words, we prove necessary and sufficient optimality conditions for a feasible solution to be an ?-efficient solution (an approximate efficient solution) of the robust multiobjective optimization problem.Moreover, we use a scalarizing method in proving these optimality results. In this method,for the robust multiobjective optimization problem, its associated scalar optimization problem is constructed. Then, we prove the equivalence between an approximate efficient solution of the robust multiobjective optimization problem and an approximate solution of its associated scalar optimization problem constructed in the scalarizing method which is used in this article.The ?-efficiency theorem established in this article for the considered uncertain multiobjective programming problem is illustrated by an example of such a vector optimization problem with the uncertainty in both objective and constraint functions.
2 Preliminaries
The following convention for equalities and inequalities will be used throughout this article.
For any vectors x=(x1,...,xn)T,y =(y1,...,yn)Tin Rn,we give the following definitions:
(i) x=y if and only if xi=yifor all i=1,...,n;
(ii) x (iii) x ≦y if and only if xi≦yifor all i=1,...,n; (iv) x ≤y if and only if x ≦y and In this section, we provide some definitions and results that we shall use in the sequel. The inner product in Rnis defined by 〈x,y〉:=xTy for all x,y ∈Rn: The set C is convex whenever λx+(1 ?λ)y ∈C for all x,y ∈C and any λ ∈[0,1]. The set C ?Rnis a cone if αC ?C for all α ≧0. The indicator function δC:Rn→R ∪{+∞} of a set C is defined by A function f :Rn→R∪{+∞}is said to be convex on Rnif the inequality f(λx+(1?λ)y)≦λf(y)is satisfied for all x,y ∈Rnand any λ ∈[0,1].The effective domain of f,denoted by domf,is defined by domf :={x ∈Rn:f(x)<+∞}.The epigraph of the function f :Rn→R∪{+∞},denoted by epif, is defined by Let f :Rn→R∪{+∞}be a convex function. The ?-subdifferential of f at∈domf is defined by Let f be a proper convex function on Rn. Its conjugate function f?: Rn→R ∪{+∞} is defined at x?∈Rnby Clearly, f?is a proper lower semicontinuous convex function and, moreover, Proposition 2.1([25, 32]) Let f1: Rn→R be a continuous convex function and f2:Rn→R ∪{+∞} be a proper lower semicontinuous convex function. Then, Proposition 2.2([25]) Let fi,i ∈I,(where I is an arbitrary index set)be a proper lower semicontinuous convex function on Rn.Furthermore,assume that there exists∈Rnsuch that. Then, Now, let gj(·,vj) : Rn×Rq→R,vj∈Vj?Rq,j = 1,...,m, be convex functions. Then,the set is called a robust characteristic cone. Proposition 2.3([25]) Let gj: Rn×Rq→R,j = 1,...,m, be a continuous function,such that for each vj∈Vj?Rq,gj(·,vj) is a convex function. Then, the following set is a cone. Proposition 2.4([25]) Let gj: Rn×Rq→R,j = 1,...,m, be continuous functions and, for each j = 1,...,m,Vj?Rqbe a convex set. Furthermore, assume that, for each vj∈Vj,gj(·,vj) is a convex function on Rnand, for each x ∈Rn,gj(x,·) is a concave function on Vj. Then, is a convex cone. Proposition 2.5([21, 32]) Let f : Rn→R ∪{+∞} be a proper lower semicontinuous convex function and∈domf. Then, Proposition 2.6([25]) Let gj:Rn×Rq→R,j =1,...,m,be continuous functions such that, for each vj∈Vj?Rq,gj(·,vj) be a convex function on Rn. Furthermore, assume that each set Vj,j = 1,...,m, is compact, and there exists∈Rnsuch that gj(,vj) < 0 for any vj∈Vj,j =1,...,m. Then, the set is closed. In this section, we derive both necessary and sufficient optimality conditions for a feasible solution to be an ?-robust efficient solution of the considered uncertain multiobjective programming problem with the uncertainty in both objective and constraint functions by examining its robust (worst-case) counterpart, that is, its associated robust multiobjective programming problem. In this article, we consider an uncertain multiobjective programming problem defined as follows: where fi: Rn×Rp→R,i = 1,...,s, and gj: Rn×Rp→R,j = 1,...,m, are continuous functions and ui∈Ui,vj∈Vj, are uncertain parameters,that is,the data vectors uiand vjare not known exactly at the time when the solution has to be determined, Uiand Vjare convex compact subsets of Rpand Rq, respectively. Hence, the robust counterpart (RMP) of the uncertain multiobjective programming problem (UMP) is defined as the following multiobjective programming problem: Let us denote by S the set of all feasible solutions for the robust multiobjective programming problem (RMP), that is, S ={x ∈Rn:gj(x,vj)≦0,j =1,...,m,?vj∈Vj}. Definition 3.1A point x ∈Rnis a robust feasible solution of the considered uncertain robust multiobjective programming problem (RMP) if gj(x,vj)≦0,j =1,...,m,?vj∈Vj. Now,we give the definition of ?-efficiency(approximate efficiency)for the defined uncertain robust multiobjective programming problem (RMP) which is, at the same time, a robust ?efficient solution of the original uncertain multiobjective programming problem (UMP). Definition 3.2(?-efficient solution of (RMP)) Let ? ∈Rs,? ≧0 be given. A point∈S is said to be an ?-efficient solution of the robust multiobjective programming problem (RMP)(thus, a robust ?-efficient solution of the considered uncertain multiobjective programming problem (UMP)) if there is no a feasible solution x of (RMP) such that In this article, we shall assume that, for any ? ∈Rs,? ≧0, the set of ?-efficient solutions of the robust multiobjective programming problem (RMP) is nonempty. Now, for the considered uncertain robust multiobjective programming problem(RMP), we define its associated scalar optimization problem. Now, we give the definition of a γ-optimal solution of the scalar optimization problem(SMRP?). Definition 3.3Let γ be a given nonnegative real number. A feasible pointof the scalar optimization problem (SMRP?) is said to be a γ-optimal solution of the scalar optimization problem (SMRP?) if the inequality holds for all feasible solutions of the problem (SMRP?). Now, we prove the equivalency between the problems (RMP) and (SMRP?). Lemma 3.4Let ? ≧0 be given. Then,∈S is an ?-efficient solution of (RMP) if and only ifis a γ-optimal solution of (SMRP?), where ProofLetbe an ?-efficient solution of(RMP). Asis an ?-efficient solution of(RMP),by Definition 3.2, there is no other feasible solution x ∈S such that This means that there is no x ∈satisfying both (3.1) and (3.2). Then, by (3.1) and (3.2),it follows that the inequality is not fulfilled for any x ∈. Thus,by Definition 3.3,this means thatis a γ-optimal solution of (SMRP?). Now, we extend the result established by Jeyakumar and Li (Theorem 2.4 [25]) to the vectorial case. Lemma 3.5Let fi(·,ui),i = 1,...,s, be a convex and continuous function and gj:Rn×Rn→R,j =1,...,m, be a continuous function such that, for each vj∈Vj, where Vjis a compact subset of Rq,gj(·,vj) is a convex function. Furthermore, assume that S is nonempty.Then, exactly one of the following two statements holds: ProofAssume that condition (ii) is fulfilled. Then, the following relation By Proposition 2.2, it follows that Then, by Proposition 2.1, (3.7) is equivalent to Thus, by the definition of the epigraph, we have Hence, by the definition of the conjugate function, (3.9) is equivalent to By the definition of an indicator function, it follows that δA?(x) = 0 for any x ∈. Hence,(3.10) is equivalent to F(x) ≧0 for any x ∈. Thus, we have shown that the case when the condition (ii) is fulfilled is equivalent to the fact that the condition (i) is not satisfied. This completes the proof of this lemma. Now, we use Lemma 3.5 to prove the next result. Theorem 3.6Let fi: Rn×Rp→R,i=1,...,s, be continuous functions such that, for each ui,fi(·,ui) is a convex function. Also, let gj: Rn×Rq→R,j = 1,...,m, be continuous functions such that, for each vj∈Rq,gj(·,vj) is a convex function. Furthermore, assume that the set is closed and convex. Then,is a γ-optimal solution of (SMRP?), if and only if there existsuch that the following inequality ProofLetbe a γ-optimal solution of(SMRP?). Then,by Definition 3.2,it follows that the inequality F(x) ≧F()?γ holds for all x ∈, whereLet H(x)=F(x)?F()+γ. Then, by the above inequality, the inequality Using the definition of the function H, (3.13) can be re-written as follows: Thus, (3.14) gives Again by using the definition of the conjugate function, (3.15) yields By(3.12),it follows that the condition(i) in Lemma 3.5 is not satisfied. Hence,by Lemma 3.5,it follows that the condition (ii) is fulfilled, that is, the relation holds. By assumption, the set is closed and convex. Thus, (3.17) gives By (3.18), it follows that there existsuch that the relation holds. Then, there exist t?∈Rn,a ≧0,∈Rn,bi≧0,i = 1,...,s,∈Rn, and cj≧0,j =1,...,m, such that Hence, the above relation yields, respectively, and By (3.19), it follows that Combining(3.20)and(3.21),and by the definition of a conjugate function,then we obtain that the relation holds for any x ∈Rn. Then, (3.22) yields By the definition of a conjugate function for the functionswe have By the definition of the function F, it follows that the inequality Conversely, assume that there exist≧0,i = 1,...,s,∈Vj,j = 1,...,m, such that inequality (3.11) is fulfilled for any x ∈. As≧0,i = 1,...,s,≧0,j = 1,...,m, and x ∈, (3.11) implies that Using Lemma 3.4 and Lemma 3.5, we prove the following ?-efficiency theorem for the considered robust multiobjective programming problem (RMP). Theorem 3.7(?-efficiency theorem) Let fi: Rn×Rp→R,i = 1,...,s, be continuous functions such that, for each ui, every function fi(·,ui) is convex. Also, let gj: Rn×Rp→R,j =1,...,m, be continuous functions such that, for each vj∈Rq, every function gj(·,vj) is convex. Furthermore, assume that the setis closed and convex. Then, the following statements are equivalent: (i) x ∈S is an ?-efficient solution of the robust multiobjective programming problem(RMP); and ProofThe equivalency between the conditions (i) and (ii) follows by Theorem 3.6. Now, we prove the equivalency between the conditions (ii) and (iii). Now, we prove the equivalency of conditions (iii) and (iv). Let us assume that the condition (iii) is fulfilled, that is, (3.18) is satisfied. Hence, by(3.18), it follows that there existsuch that the relation holds. Then, by Proposition 2.5, it follows that there exist≧0,i=1,...,s,≧0,∈Vj,j =1,...,m, such that holds. The above relation implies equivalently that there existsuch that and Relation (3.25) is equivalent to the fact that there existj =1,...,m, such that Hence, (3.27) and (3.26) are precisely the condition (iv). Thus, the proof of this theorem is completed. In order to illustrate the results established in Theorem 3.7, we give the example of an uncertain multiobjective programming problem with the uncertainty in both objective and constraint functions. Example 3.8Consider the following uncertain multiobjective programming problem with the uncertainty in both objective and constraint functions defined as follows: where u1∈U1= [0,1],u2∈U2= [0,1],v1∈V1= [], v2∈V2= [?1,0] are uncertain parameters. Its robust counterpart,that is,the uncertain multiobjective programming problem(RMP1), is defined as follows: Condition (i)Note that the following inequalities, if at least one of them is strict, are not satisfied for any feasible solutionof the robust multiobjective programming problem (RMP1). Hence, by Definition 3.2,= (0,) is, in fact, an ?-efficient solution of(RMP1). Condition (ii)LetHence,. Note that the following inequalityis satisfied for all feasible solutions of the associated scalar optimization problem(SRMP?)defined for the robust multiobjective programming problem(RMP).Then,by Definition 3.3,=(0,12)is a γ-optimal solution of the problem (SRMP?). Condition (iii)By the definition of the conjugate function, we have Hence, by the definition of the epigraph of a function, we have By the definition of the epigraph of a function, Proposition 2.1, and (2.4), we have Now, we check the condition (iii). Thus, we have Condition (iv)In order to check condition (iv), we set Taking into account the calculated above ?-subdifferentials of the appropriate functions, we have Hence, it follows that Furthermore, note that also the second relation in condition (iv) is fulfilled at the considered case. Indeed, we haveThen, we have shown that condition (iv) is also fulfilled. In this article, the robust approach is used for finding approximate efficient solutions of the considered multiobjective programming problem with the uncertainty in both objective and constraint functions. Namely, we study the ?-efficiency theorem for the considered uncertain convex multiobjective programming problem by examining its robust(worst-case)counterpart.In other words,we establish both necessary and sufficient optimality conditions for an ?-efficient solution of the robust multiobjective optimization problem. In proving this result, we also use a scalarizing method. Furthermore, the ?-efficiency theorem established in this article is illustrated by the example of a nondifferentiable multiobjective programming problem with the uncertainty in both objective and constraint functions. However, some interesting topics for further research remain. Also, it would be interesting to prove similar optimality results for other classes of uncertain multiobjective optimization problems. We shall investigate these questions in subsequent papers.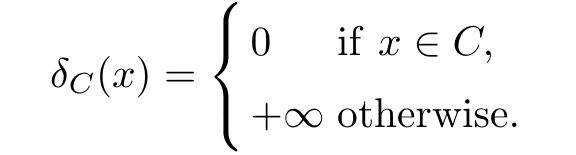
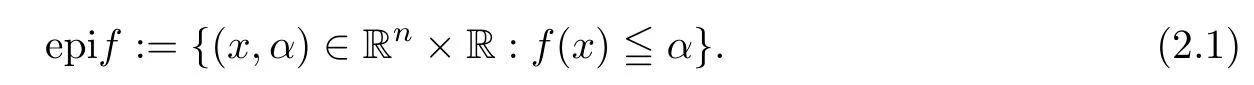
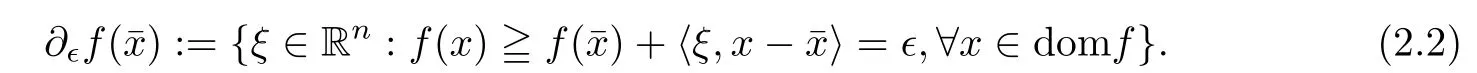
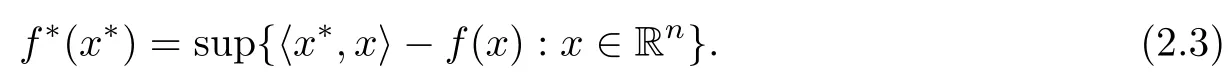
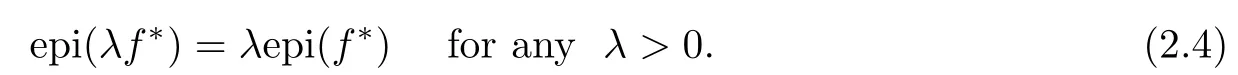

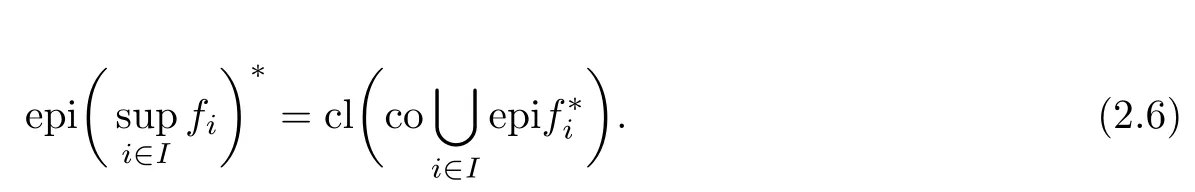
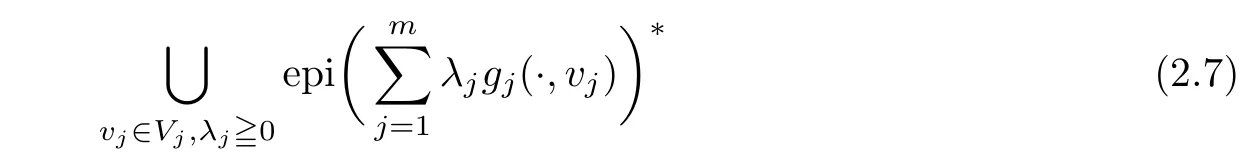
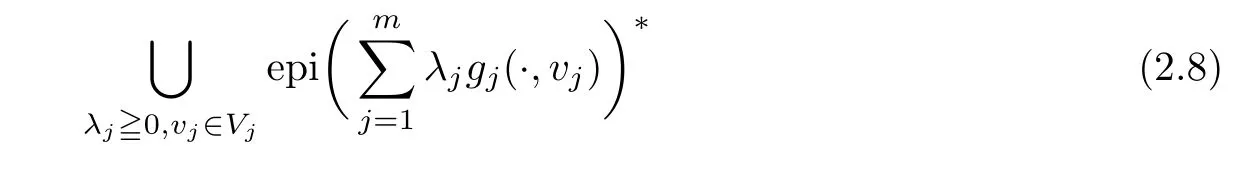

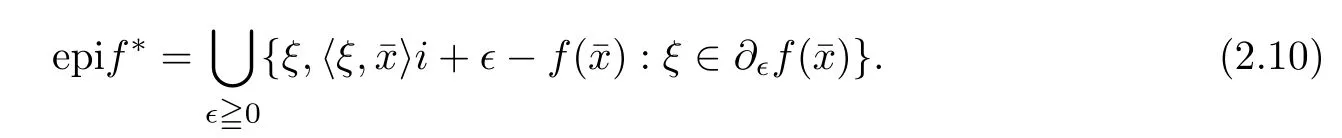
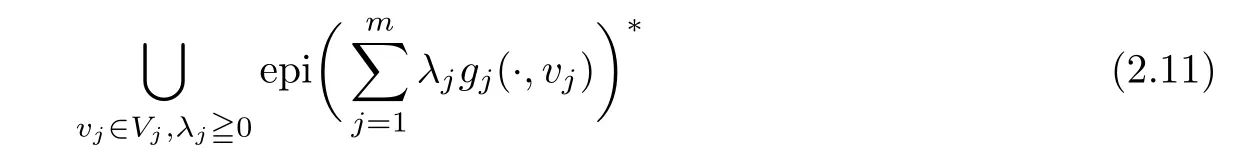
3 ?-Optimality Conditions
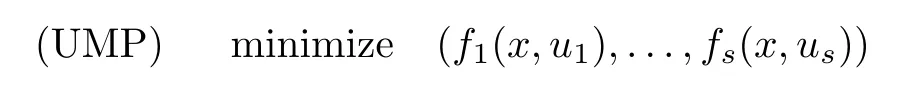
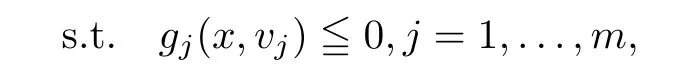
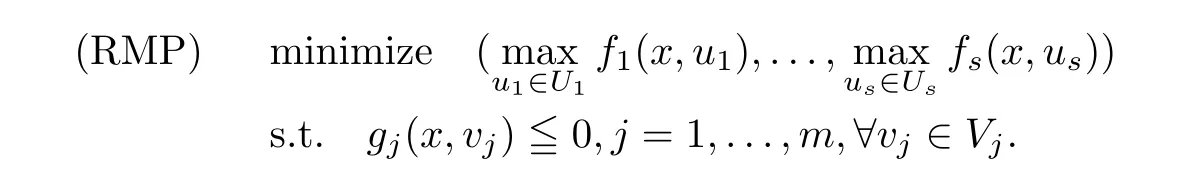
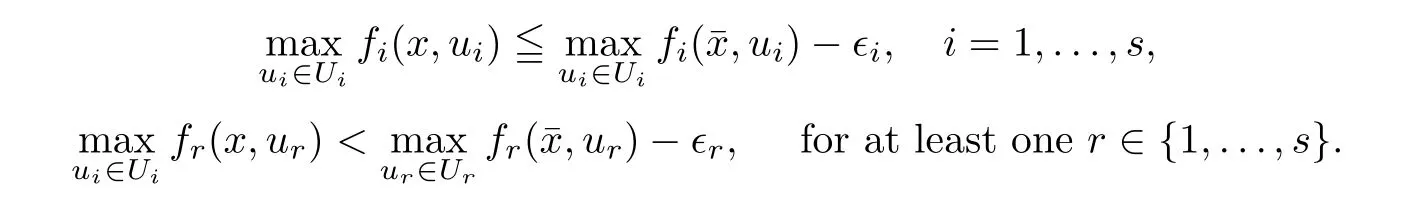
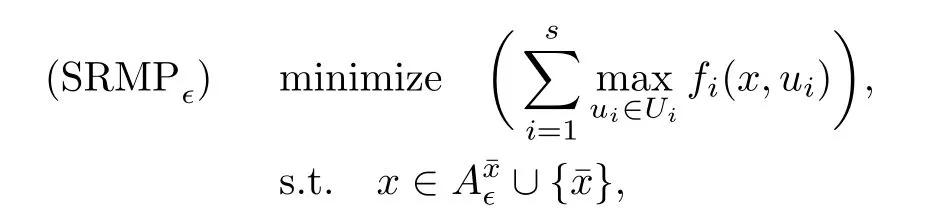
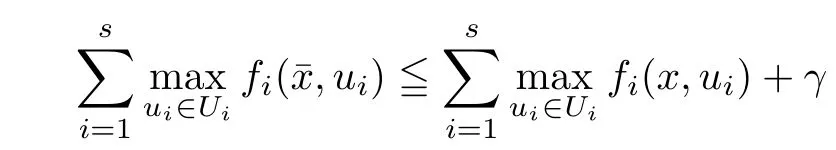
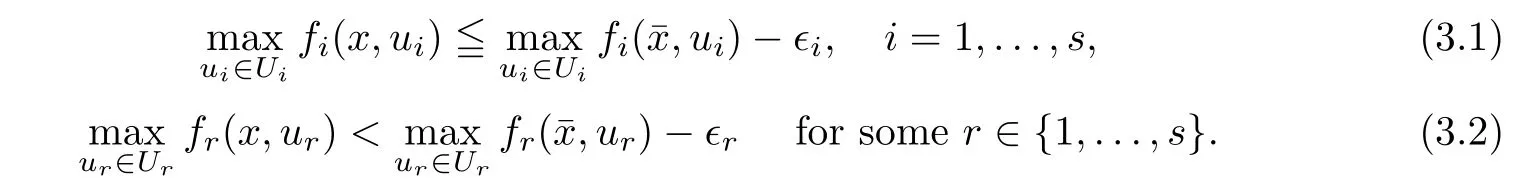

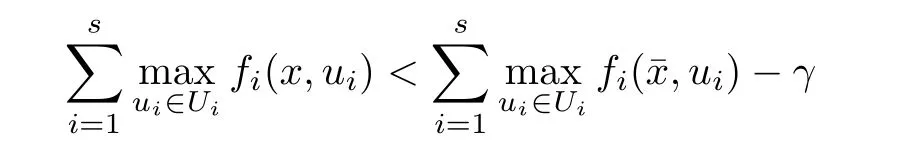

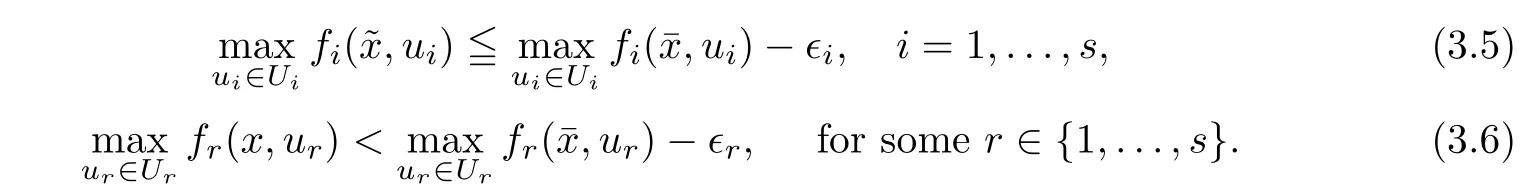
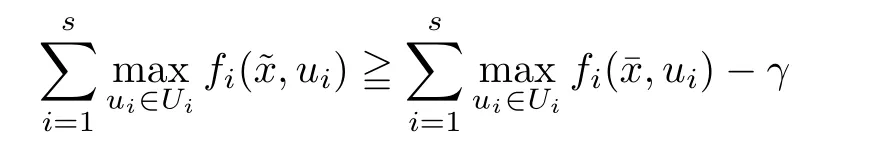
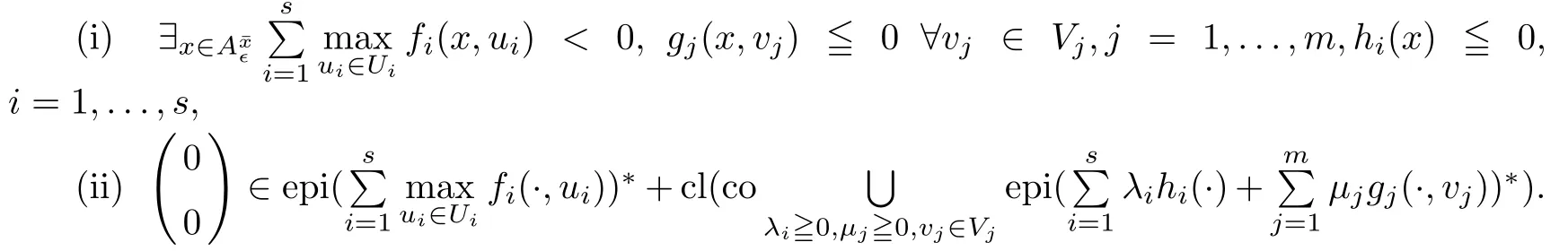

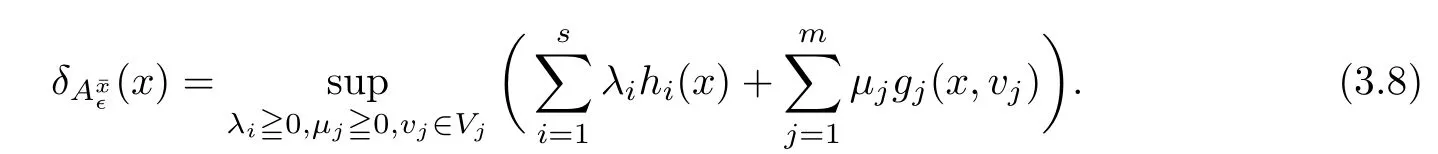

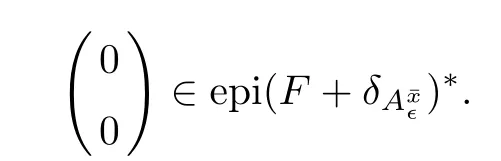

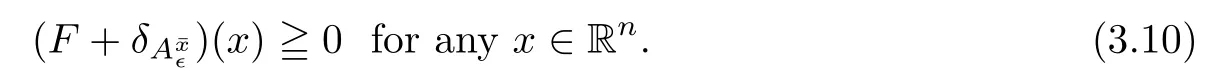
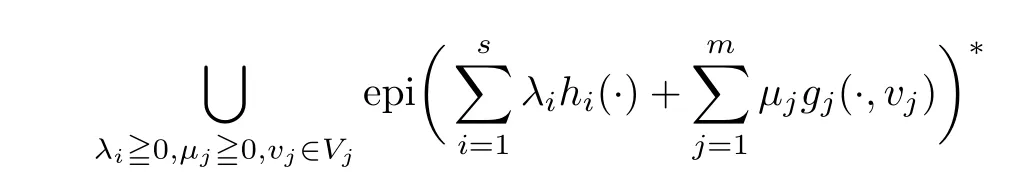
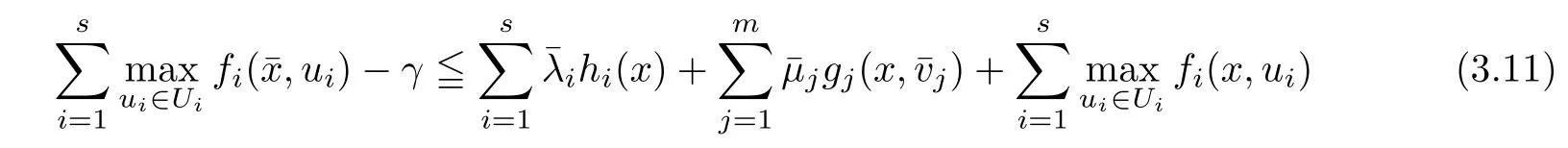

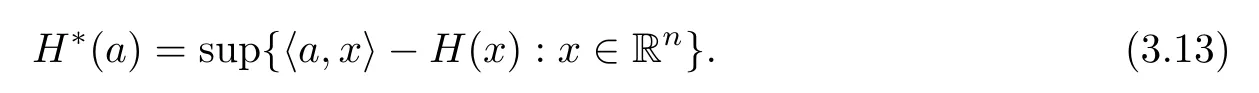



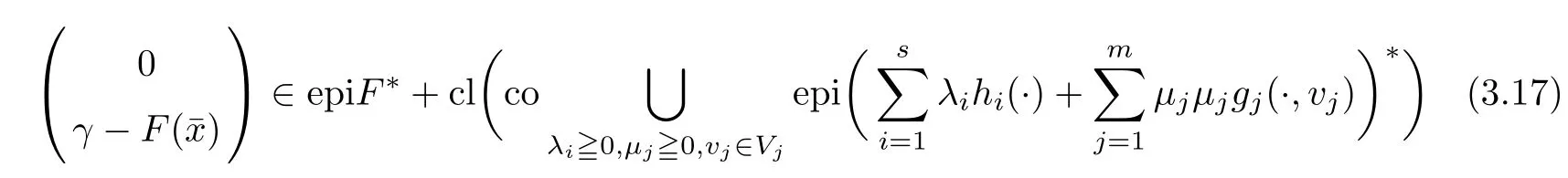
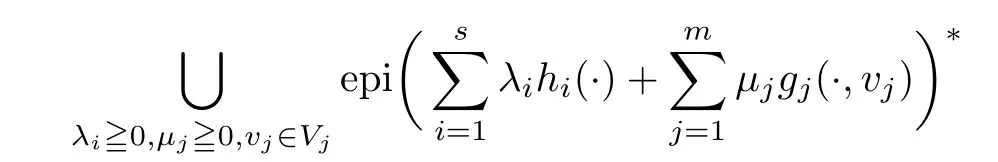
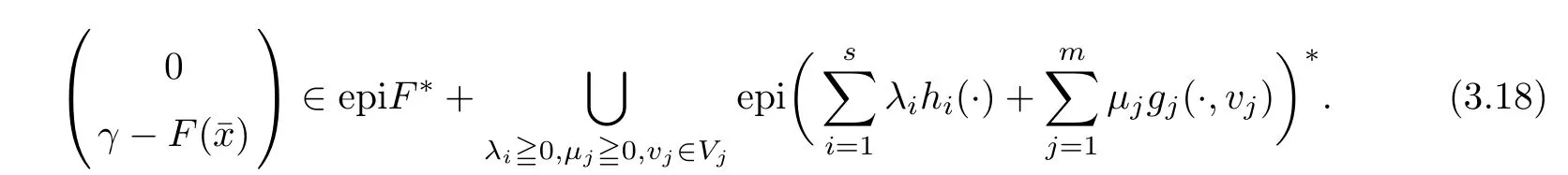
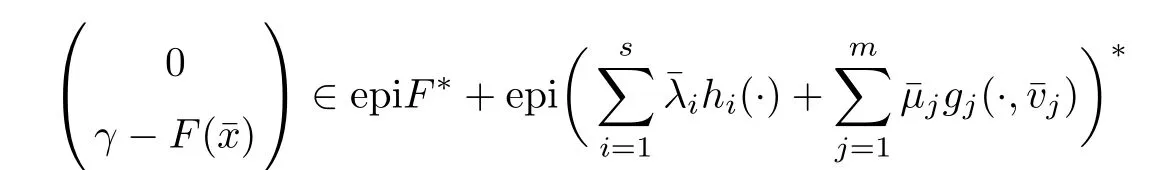
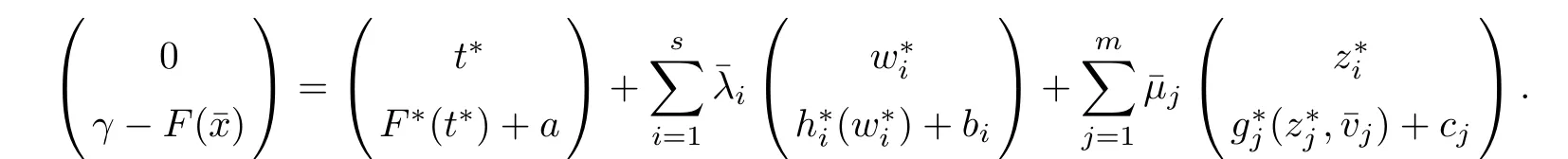

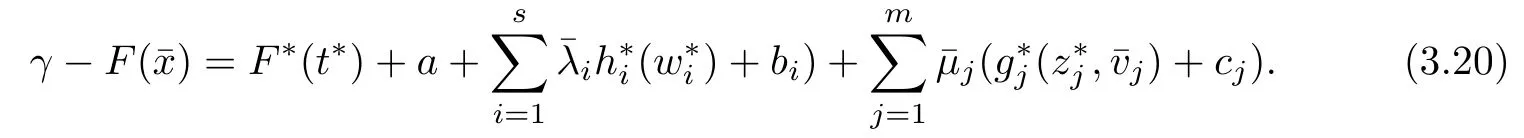

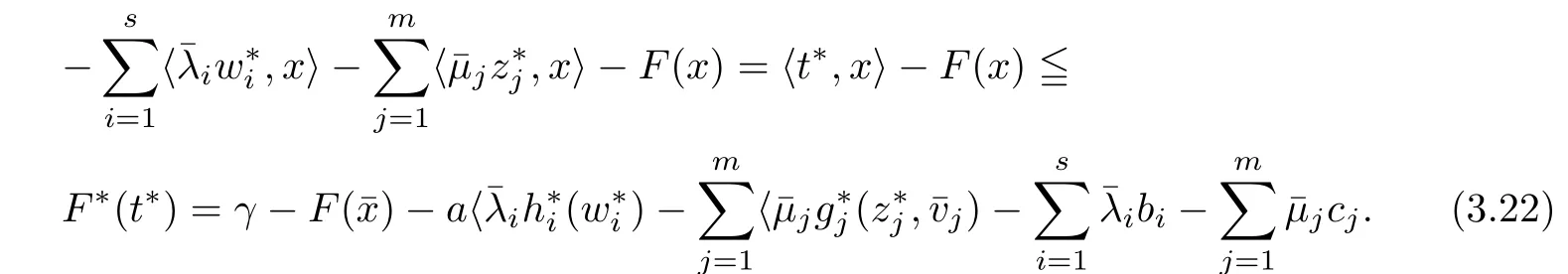
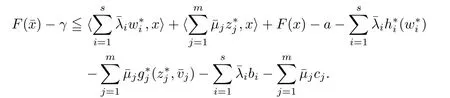
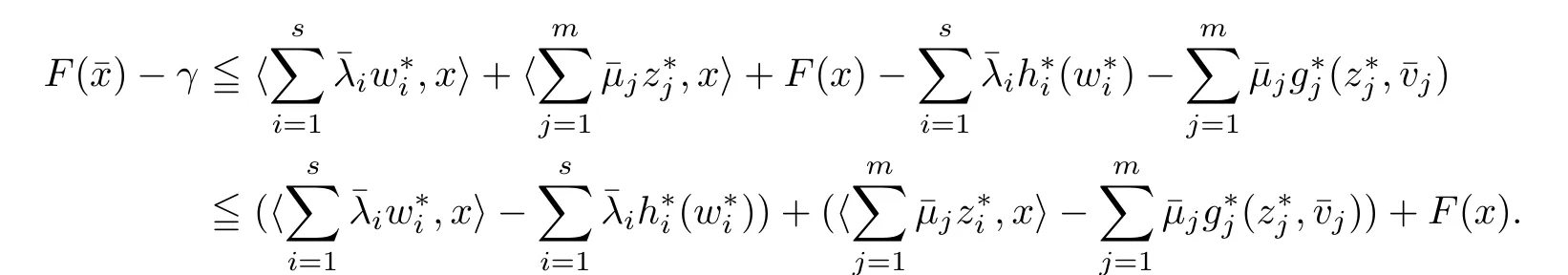

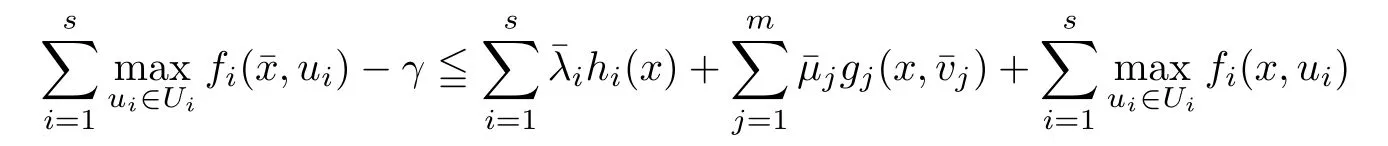
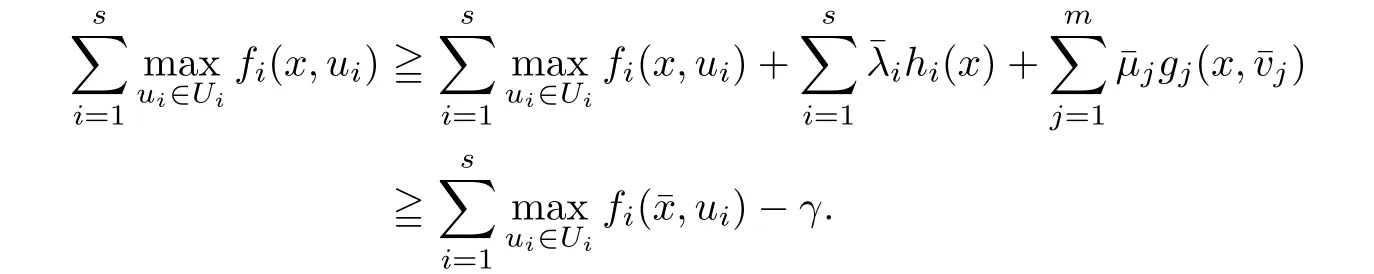
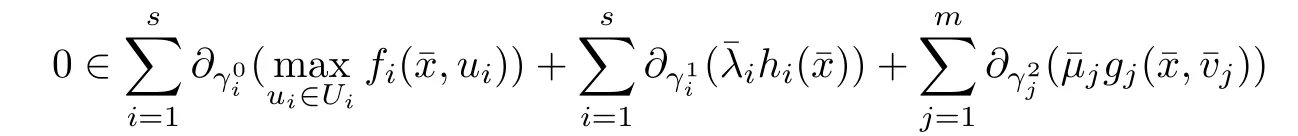
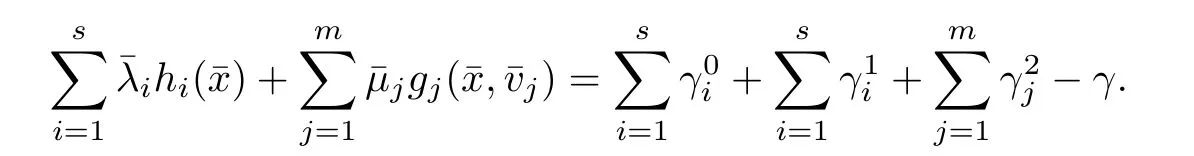
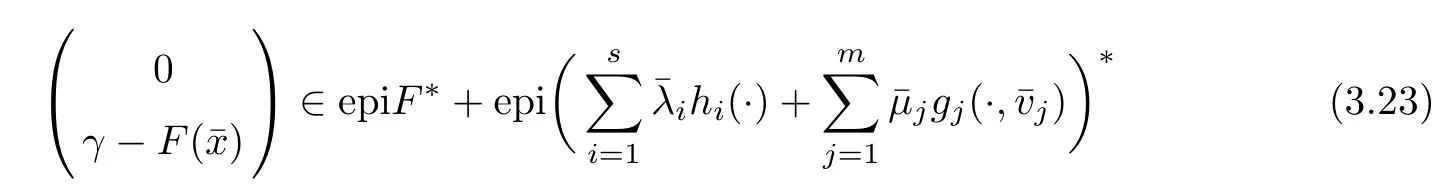
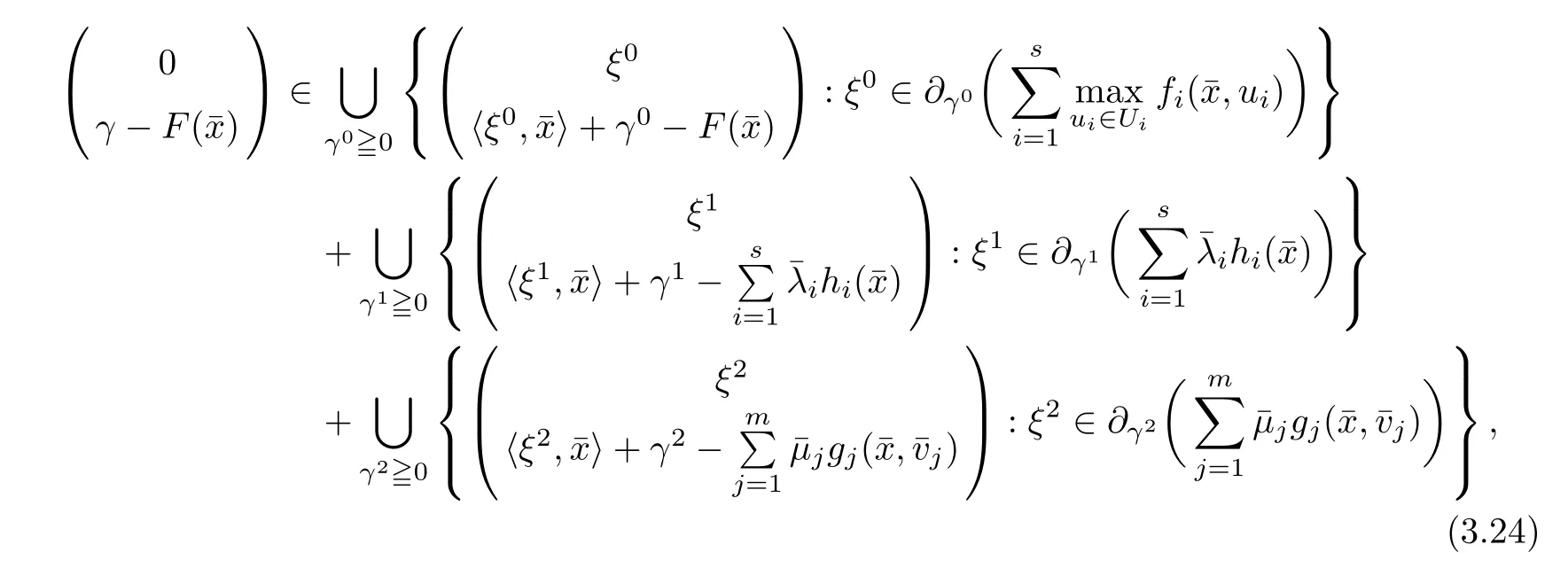
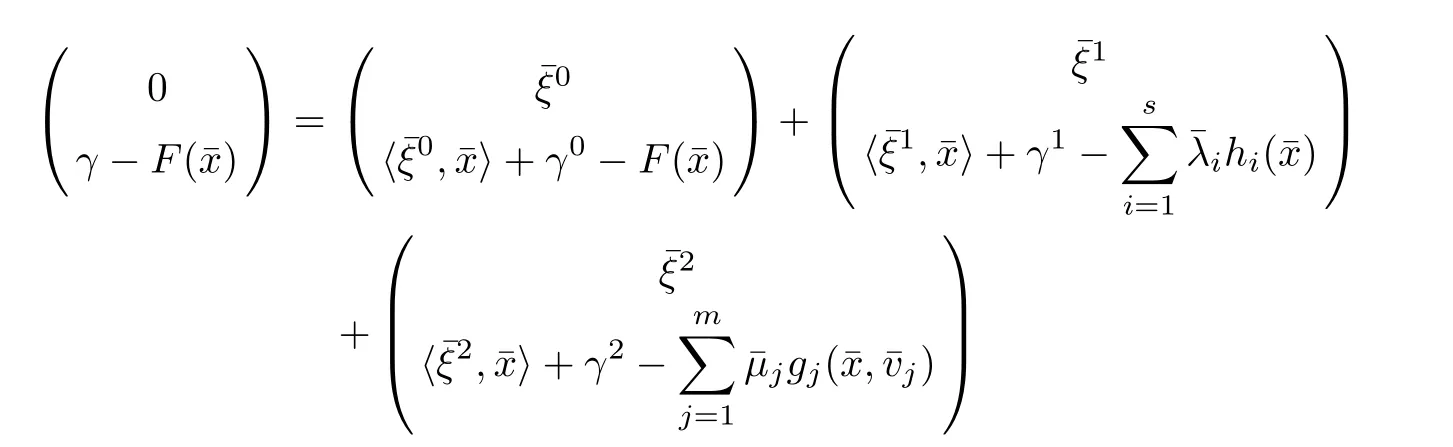
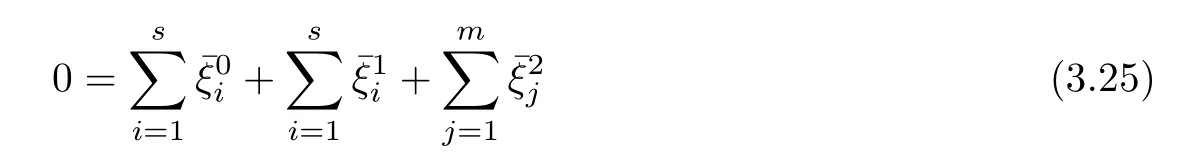


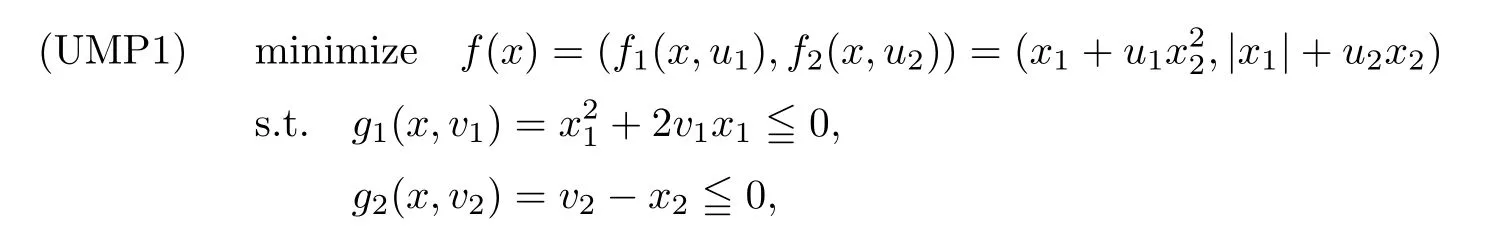

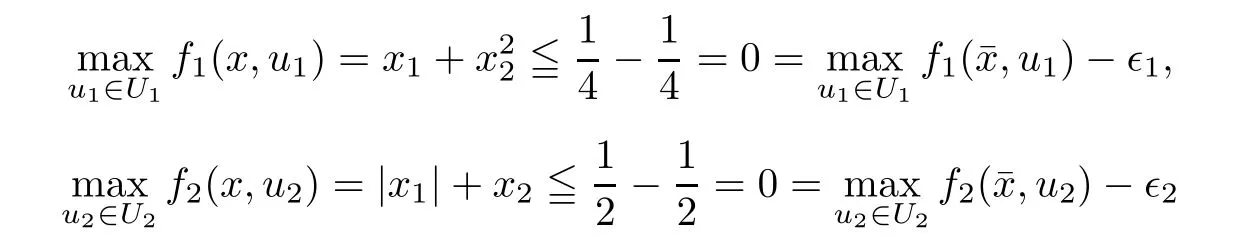
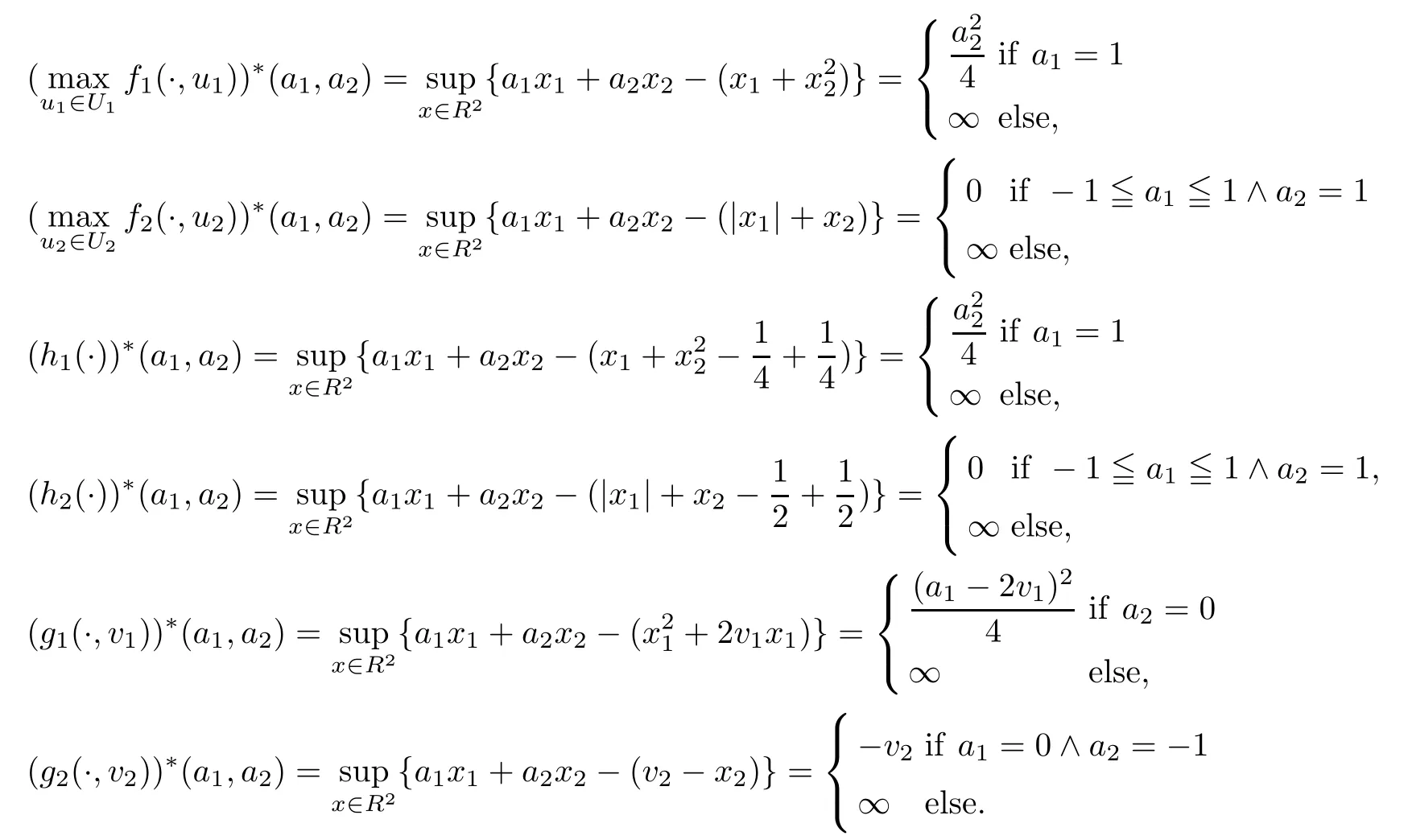


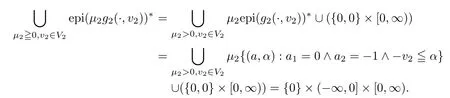
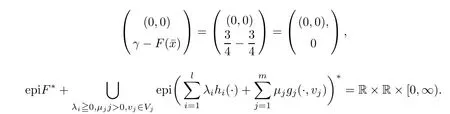
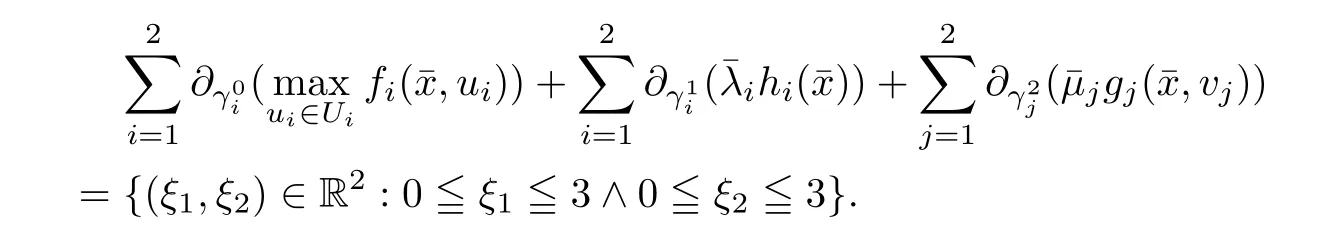
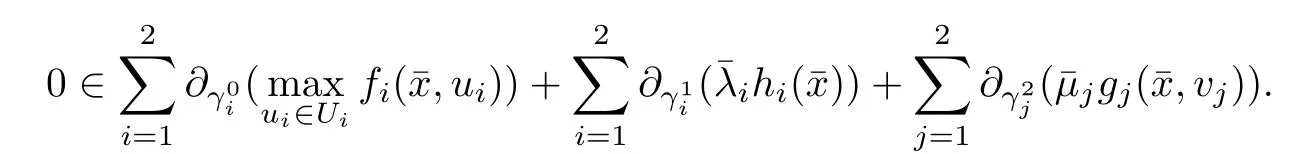
4 Conclusions
 Acta Mathematica Scientia(English Series)2020年3期
Acta Mathematica Scientia(English Series)2020年3期
- Acta Mathematica Scientia(English Series)的其它文章
- ARTIAL REGULARITY FOR STATIONARY NAVIER-STOKES SYSTEMS BY THE METHOD OF A-HARMONIC APPROXIMATION*
- ON BLOW-UP PHENOMENON OF THE SOLUTION TO SOME WAVE-HARTREE EQUATION IN d ≥ 5*
- THE QUASI-BOUNDARY VALUE METHOD FOR IDENTIFYING THE INITIAL VALUE OF THE SPACE-TIME FRACTIONAL DIFFUSION EQUATION ?
- SYNCHRONIZATION OF SINGULAR MARKOVIAN JUMPING NEUTRAL COMPLEX DYNAMICAL NETWORKS WITH TIME-VARYING DELAYS VIA PINNING CONTROL?
- ON THE ENTROPY OF FLOWS WITH REPARAMETRIZED GLUING ORBIT PROPERTY*
- ON NEW APPROXIMATIONS FOR GENERALIZED CAUCHY FUNCTIONAL EQUATIONS USING BRZDE?K AND CIEPLI′NSKI’S FIXED POINT THEOREMS IN 2-BANACH SPACES?
