Department of Mathematics,Jiangsu Normal University,Xuzhou 221116,China

E-mail:xuxian@163.com

Baoxia QIN(秦寶俠)

School of Mathematics,Qilu Normal University,Jinan 250013,China

E-mail:qinbaoxia@126.com

Zhen WANG(王震)

Department of Mathematics,Jiangsu Normal University,Xuzhou 221116,China

E-mail:1017979100@qq.com

Abstract In this article,by employing an oscillatory condition on the nonlinear term,a result is proved for the existence of connected component of solutions set of a nonlocal boundary value problem,which bifurcates from infinity and asymptotically oscillates over an interval of parameter values.An interesting and immediate consequence of such oscillation property of the connected component is the existence of infinitely many solutions of the nonlinear problem for all parameter values in that interval.

Key words Global solution branches,Leray-Schauder degree,asymptotic oscillation property

1 Introduction

Consider the differential equation with the integral boundary value condition

whereλ>0 is a parameter,r:[0,1]→(0,+∞)is continuously differentiable,f:[0,1]×R1→R1is continuous,andg1is a bounded variation function on[0,1].

During the past twenty years,the nonlocal boundary value problems have been studied extensively.Especially,some authors studied the existence of unbounded connected components of solutions sets bifurcating from infinity for various of nonlocal boundary value problems by using global bifurcation theories;see[1–3].Obviously,studying the manner of solutions branches approaching infinity is of interest.Some authors have studied the solutions branches for various boundary value problems,which approaches infinity in a manner of oscillating infinitely many times about a parameter(even an interval of parameters).Let us first recall some results in the literatures.R.Schaaf and K.Schmitt in[4]studied the existence of solutions of nonlinear Sturm Liouville problems whose linear part is at resonance.Using bifurcation methods,R.Schaaf and K.Schmitt studied the following one parameter problem

They showed that(1.2)has a connected component of solutions which bifurcates from infinity atλ=1,and showed that this connected component must cross theλ=1 parameter plane infinitely often.

F.A.Davidson and B.P.Rynne in[5]studied the boundary value problem

wheref:R+=[0,∞)→R1is Lipschitz continuous andλis a real parameter.Set

1)Ccan oscillate infinitely atμ0=1 if and only ifβ+=β?;

2)Cwould oscillate infinitely over an intervalIifβ+>β?.

Here,as defined in[5],a continuumC?R+×C[0,1]is said to oscillate over an intervalI=[λ?,λ+]if,for eachν ∈{+,?},there exists a sequence of positive number,such thatasn→∞,and any solution(λ,u)∈Cwithmust have,and such solutions do exist for all sufficiently largen.

Recently,in[6]we studied the solutions branches with asymptotic oscillation property for the three point boundary value problem

whereη∈(0,1),α∈[0,1),f:R+→R1is Lipschitz continuous,f(0)=0 andλis a real parameter.We showed that for small 0 6α,ifβ+>β?,(1.4)has a solution branche,which bifurcates from infinity,and asymptotically and infinitely oscillates over an intervalI.

For other references concerning the solutions branches with asymptotic oscillation property,one can refer to[7–11].Motivated by the above,in this article,we will study the solution branches with asymptotically oscillating property for(1.1).By employing an oscillatory condition on the nonlinear termf,we will prove a result for the existence of a connected component of solutions set of(1.1),which bifurcates from infinity and oscillates infinitely often over an interval ofλ-values.There are three difficulties to obtain the results about the asymptotic oscillation of connected component for(1.1).Firstly,every positive solution of(1.2)and(1.3)is symmetric aboutand has a single maximum occurring at this point.On the other hand,every positive solution of(1.4)has a single maximum point which is near toassmall enough.These play important roles in the proof of[4,5,6].However,the single maximum point of every positive solution of(1.1)is unknown and the positive solution of(1.1)may not be symmetric aboutTo overcome this difficulty,in this article we will employ a new type of conditions on the nonlinearityf.Secondly,to obtain the main results of this article,we need to study the eigenvalue problem corresponding to(1.1).However,as best as we known,there were few results on the eigenvalue problems for integral boundary value problems yet.In Section 2,we will employ a methods similar to[12]to study the eigenvalue problem(2.1)with a integral boundary value condition.Thirdly,as the nonlinearityfin(1.1)may not be of asymptotically linear type,the corresponding nonlinear operator may be non-differentiable when one converts(1.1)into an operator equation,and the methods in Rabinowitz’well known global bifurcation theorems from[13]establishing existence results for unbounded connected components bifurcating from infinity do not seem to work in our situation.Because of the contributions of Schmitt,Berestycki et al.,during the past forty years,significant progress on the nonlinear eigenvalue problems for non-differential mappings has been achieved;see[14,15]and the references therein.In this article,for the conveniences of the readers,we will give a detailed proof of the existence of connected component of solutions set of(1.1)bifurcating from infinity.Some new techniques will be developed in Section 3 of this article to overcome the third difficulty.

2 Some Preliminary Results

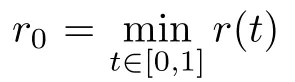
(H0)g1is increasing on[0,1],and its bounded variation on the interval[0,1]satisfies

(H1) There exist positive numbersζ?andζ+,nonnegative and continuous functionsm0(t)andm1(t),such thatand for

(H2) There exist an increasing sequence of positive numbers{ζi},and positive numbersκ,γ+,γ?>0,such that

ζi→∞asi→∞,for alliand fort∈[0,1],

In the sequel,we always assume that(H0)holds.First,we study the eigenvalue problem corresponding to(1.1)

Denote bythe sequence of the eigenvalues of the problem

Denote bythe sequence of the eigenvalues of the problem

It is well known thatasn→∞fori=1,2,forn=1,2,···,and fori=1,2,

Lemma 2.1The problem(2.2)has the first eigenvalueλ1,satisfying

ProofTo show Lemma 2.1,we will follow some ideas in[12].Letu(t,λ)be the unique solution,on[0,1],of the initial value problem

Define the Liyapunov function ofu(t,λ)as

Obviously,E[t,λ]>0 and fort∈[0,1],

Thus,we have

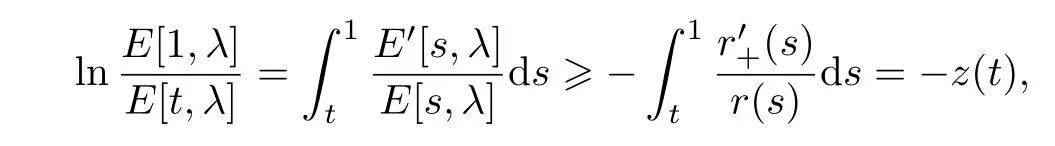
and so,

Let

Obviously,we have

and

Similarly,aswe haveBy the continuity of Γ(λ),there existssuch that Γ(λ1)=0.

Letθ(t,λ)be the Prüfer angle ofu(t,λ).Then,θ(t,λ)is a continuous function on[0,1]×R1and satisfies

It is well known(see[16,Theorem 4.5.3])that fort∈(0,1),

As

θ(t,λ1)is strictly increasing inton[0,1].Note thatSo,u′(t,λ1)has an unique zero pointt0in(0,1).Moreover,u(t,λ1)has no zero point in(0,1).Therefore,λ1is the first eigenvalue of(2.2)such that.Hence,the proof is complete.

Remark 2.1The linear eigenvalue problems with a nonlocal boundary value condition have been studied by some authors in recent years;see[3,12,17]and the references therein.Here,for our purpose,we only studied the first eigenvalue of(2.2).Obviously,one can still study other eigenvalues of(2.2)under more general condition onrandg1.

Let

andSP=S∩P.Define the operatorsK,T0,T1:C[0,1]→C[0,1]by

whereG(t,s)=min{t,s}(1?max{t,s})fort,s∈[0,1].Obviously,T0,T1:C[0,1]→C[0,1]are completely continuous operators.

Lete0(t)=G(t,t)andfort∈[0,1].Note thatK:P→PandBy(2.6),we haveand

Lemma 2.2Foris completely continuous,whereQ=

ProofWe only need to check thatIn fact,it is easy to see that

So,we have forx∈P,

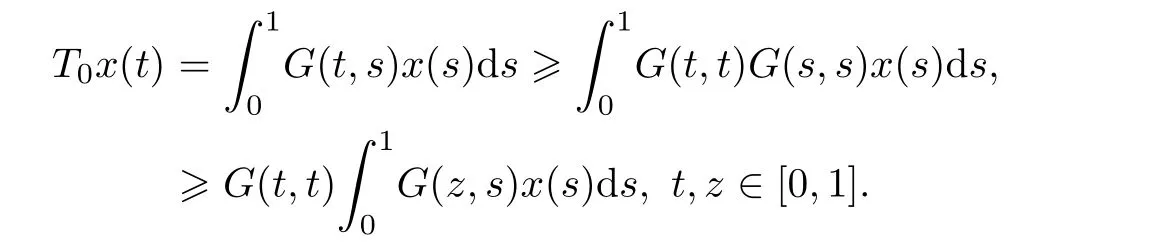
Asz∈[0,1]is arbitrarily given,we have

It follows from(I?K)?1(P)?Pthat

By(2.6),we have

and so

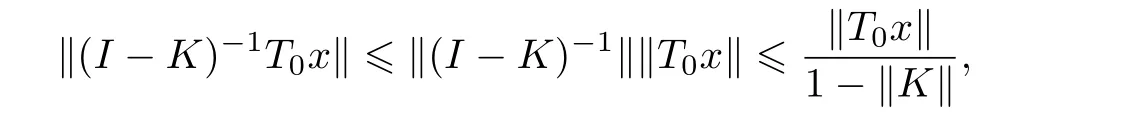
that is

It follows from(2.7)and(2.8)that

Define the operatorsby

wherex+(t)=max{x(t),0}fort∈[0,1].Obviously,x∈P{θ}is a solution of(1.1)if and only ifx=A(λ,x).

Lemma 2.3Suppose that(H1)holds.Letforand

forThen,forand

ProofAssume by make contradiction that(2.9)does not hold.Then,there existsuch thatIt follows from(H1)that

Thus,by Lemma 2.2,we have

and so,

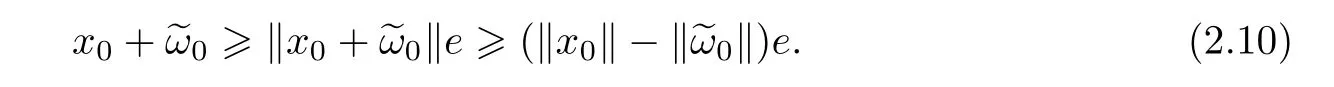
Obviously,fort∈[0,1],we have

It follows from(2.10)that

Note thatBy(2.6)and(2.10),we have fort∈[0,1],

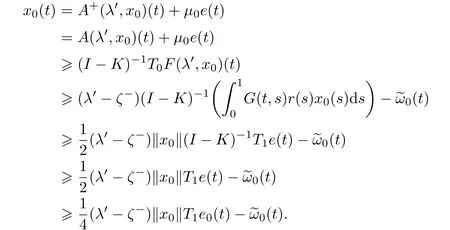
Thus,we have

and so,

which is a contradiction.Thus,(2.9)holds.The proof is complete.

Lemma 2.4Suppose that(H1)holds.Letand for

ProofFor each(λ,x)∈Swithwe have by(H1),

Note that.And so,for each(λ,x)∈Swithwe have

and thus,The proof is complete.

3 Main Results

Let

whereis the second eigenvalue of(2.3).It follows from(2.1)that

and thus Λ2>0.If

thenλ?(g1)<λ+(g1).

Now,we have the following main result.

Theorem 3.1Suppose that(H0)–(H2)and(3.1)hold.LetThen,there exists a connected componentCof,such thatCbifurcates from,and asymptotically and infinitely oscillates overI.

ProofNow,we divide our proof into the following two steps.

Step 1Obviously,we have

and

Consequently,we have

and thus

Now,we first prove that there exists a connected componentCofbifurcating frombe defined as in Lemma 2.3 for eachbe defined as in Lemma 2.4 for eachand let

Defineas

Using the extension theorem of continuous maps,we obtain a continuous functionJwhose domain issuch thatfor(λ,x)∈D0∪D1∪D2,andLet

Next,we show thatfor(λ,x)∈S?withIn fact,if otherwise,there exists a(λ,x)∈S?withsuch thatObviously,(λ,x)∈D2,and so

A similar way as the proof in Lemma 2.3 shows that.Thus,we have

Then,by a method as in the proof of Lemma 2.4,we can prove thatwhich is a contradiction.Thus,by Lemma 2.4,we have

By the definition ofJ,we have

By the definition ofJand Lemma 2.3,we have

and

Consequently,we have,by(3.4)and(3.5),

such that

Let It follows from(3.8)thatUsing the general homotopyinvariance property of Leray-Schauder degree,we have

Aswe have

It follows from(3.6)and(3.7)that

It follows from(3.2),(3.3),and(3.12)thatLet

For each(λ,x)∈C?∩D4,letbe the connected component ofC? ∩D5passing through(λ,x).AsC?is connected and unbounded,there must exist a,such thatis unbounded.For,by the definition ofJ,we havex=A(λ,x).It is easy to see that,and so

Step 2Becauseζi→+∞asi→∞,we may assume,without loss of generality,thatfor eachi.LetObviously,we have

andFor each(λ,u)∈Cwith,aswe have

Let?be the corresponding eigenfunction to the first eigenvalueλ1of(2.2)with∥?∥=1.Multiplying both side of(1.1)with?,and integrating over[0,1],we have

where

It follows from(H1)and(H3)that

It follows from(3.14)that

Asfor somet0∈(0,1),we can easily obtain

Obviously,we have

Using the inequalityG(t,s)>G(t,t)G(s,s)fort,s∈[0,1],we obtain

So,and thusUsing the boundary condition of(1.1),we can easily see that there existst0∈(0,1),such thatu′(t0)=0 andu(t0)=∥u∥.Thus,fort∈[0,t0],we have

Similarly,fort∈[t0,1],we have

Thus,by(3.16)–(3.19),we have

It follows from(3.13)–(3.15)and(3.20)that

Corollary 3.1Suppose that all conditions in Theorem 3.1 hold,andIis defined as in Theorem 3.1.Then,(1.1)has infinitely many solutions for eachλ∈I.

4 Example

To illustrate how our main results can be used in practice,we present the following example.

Example 4.1Consider the following problem:

andζi=(2×106)i?1fori=1,2,3,···.Let(t)=1+tandm0(t)=m1(t)=1 fort∈[0,1].Then,and(2.1)holds.So,(H1)and(H2)hold.

As

we have

This implies that(H0)holds.

It is easy to see that?1=12000κ,and

So,we have

This implies that(3.1)holds.

By direct computation we have

Similarly,we have

From the above,we see that the functionsandg1satisfy all conditions of Theorem 3.1.It follows from Corollary 3.1 that for eachproblem(4.1)has infinitely many positive solutions.