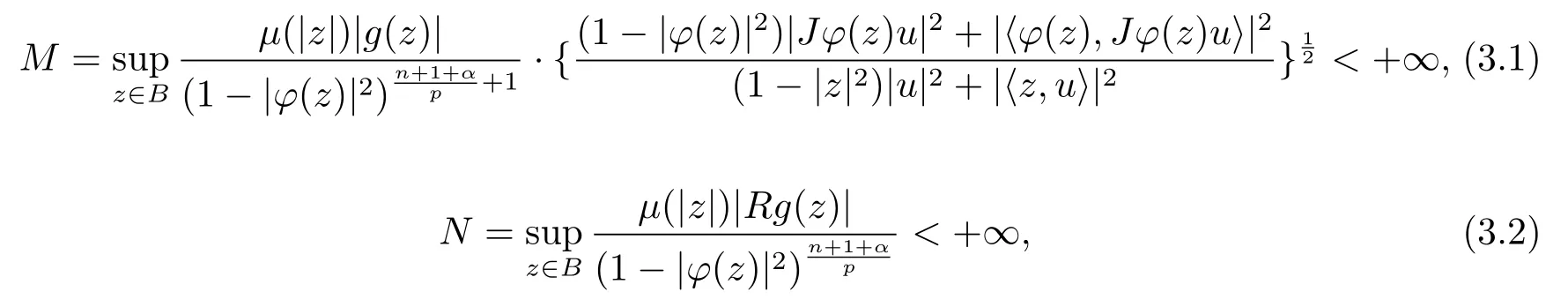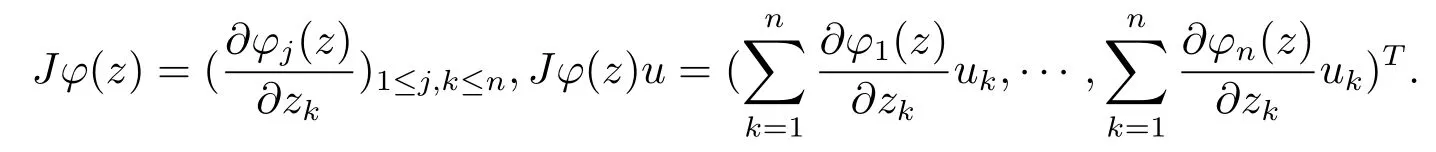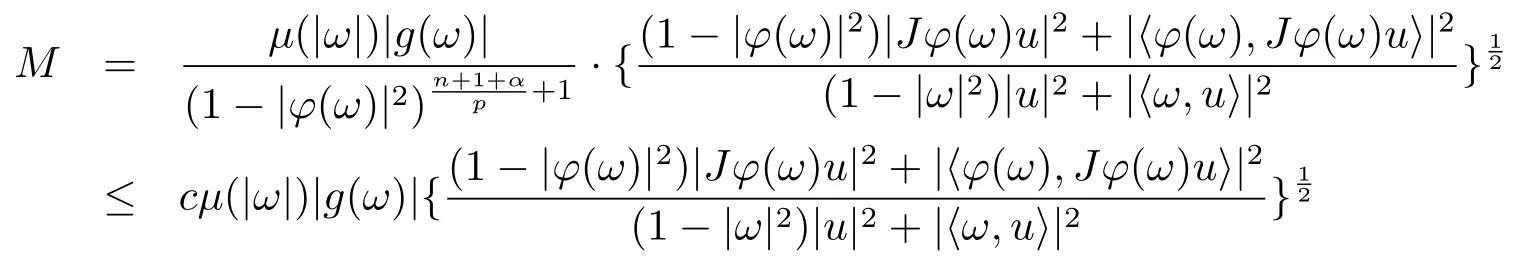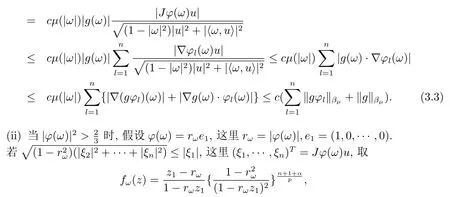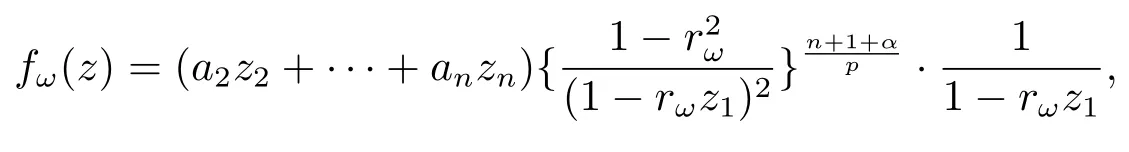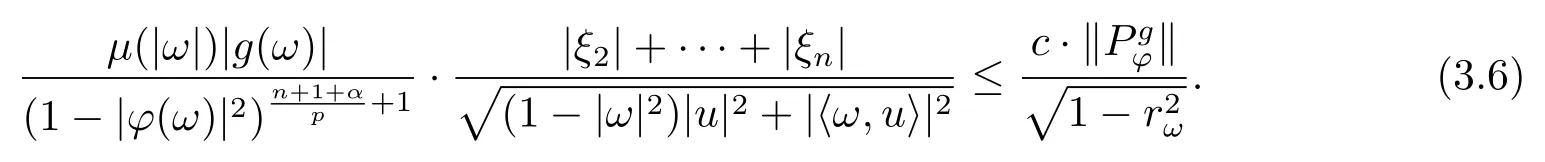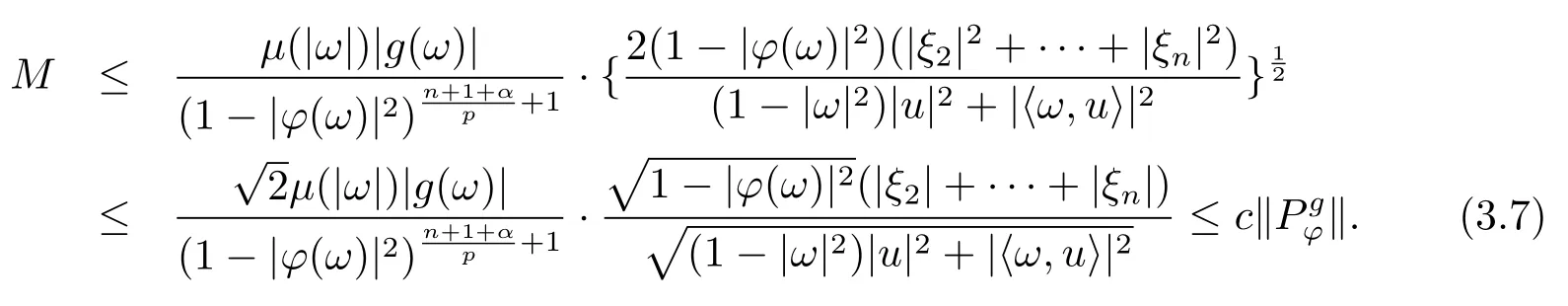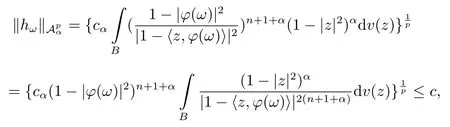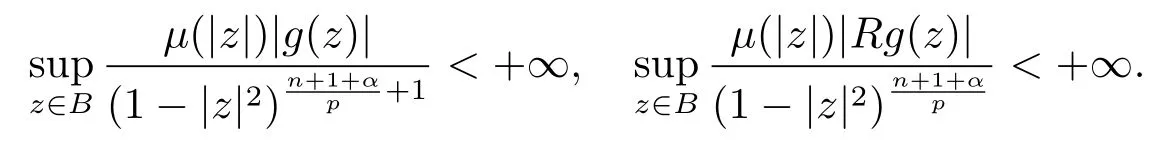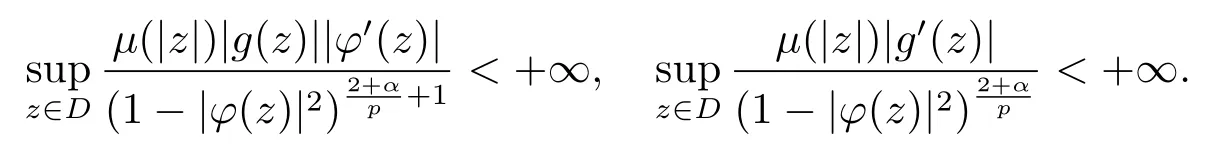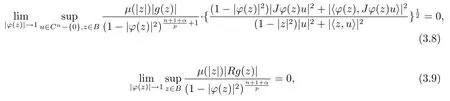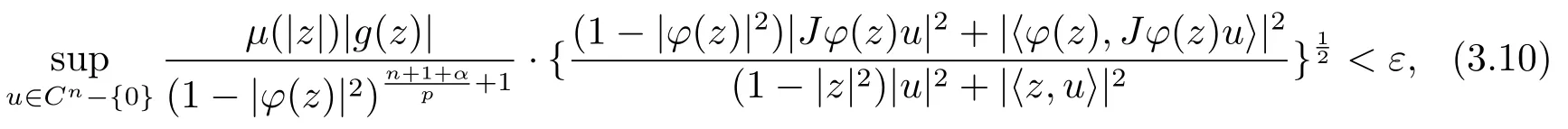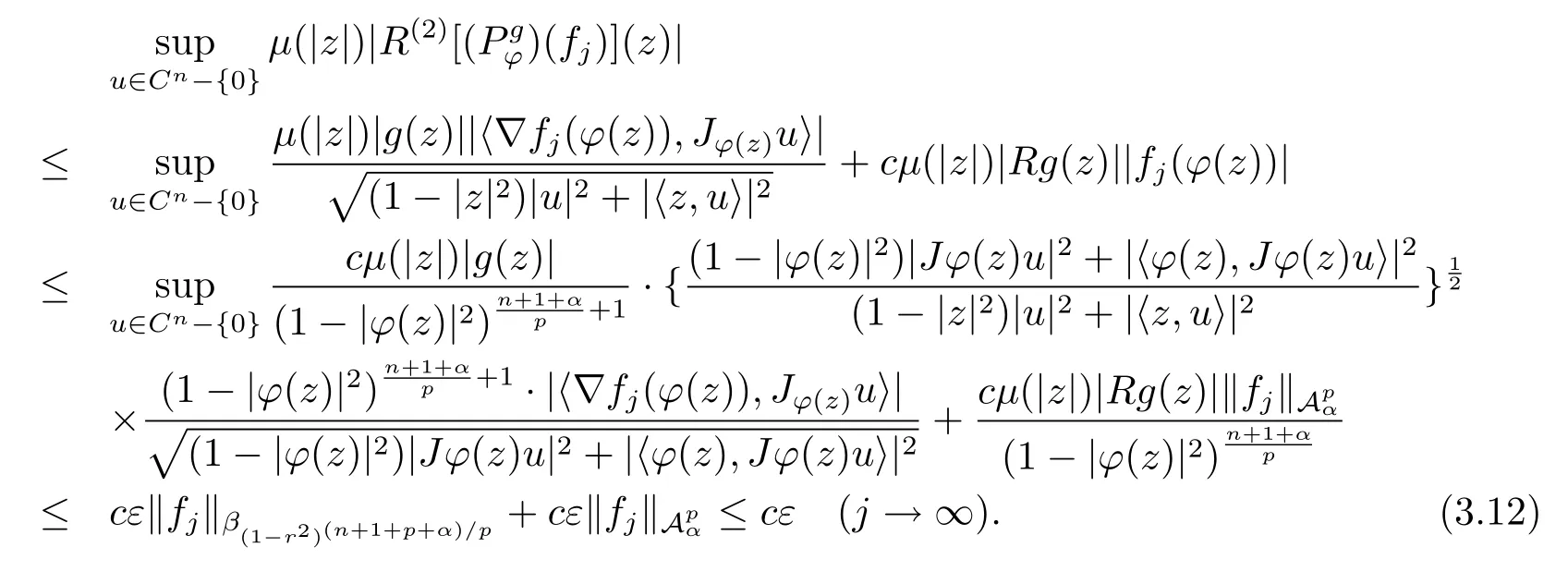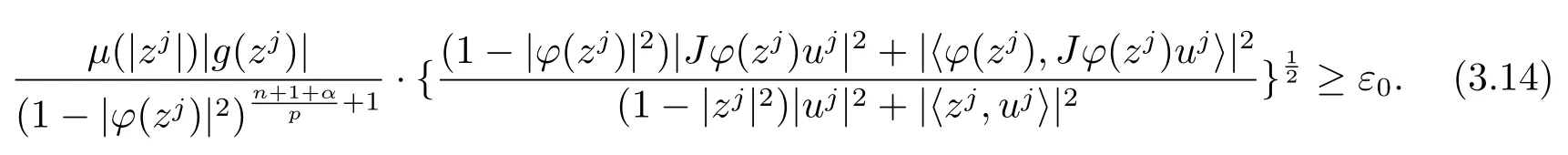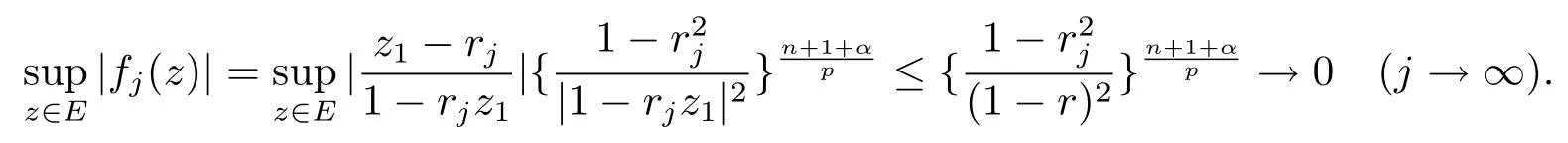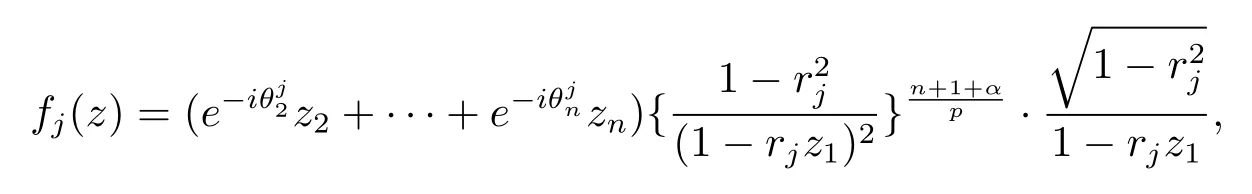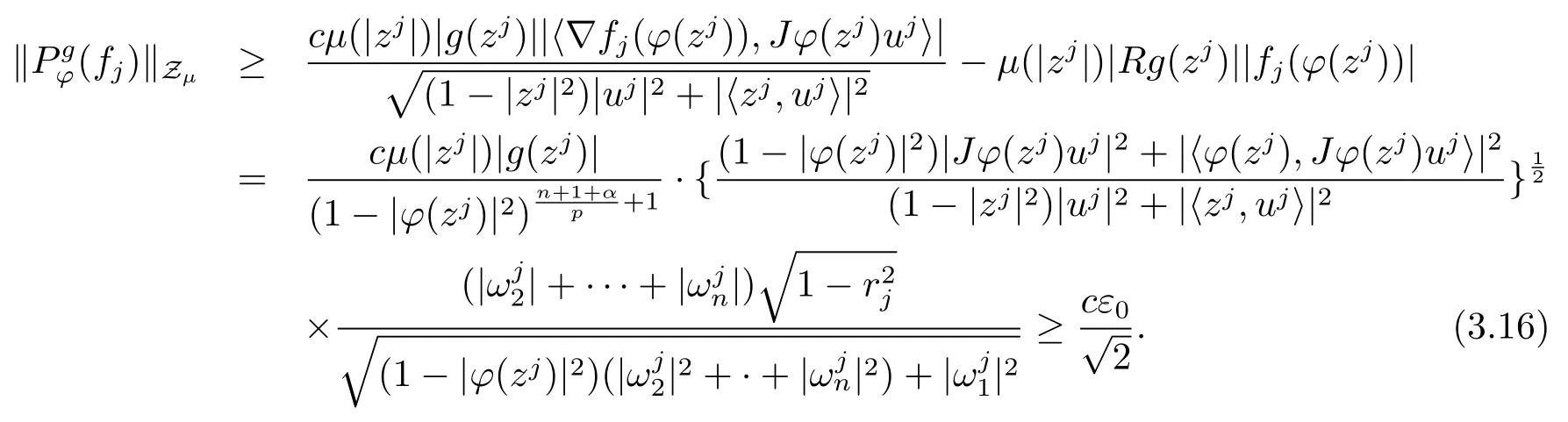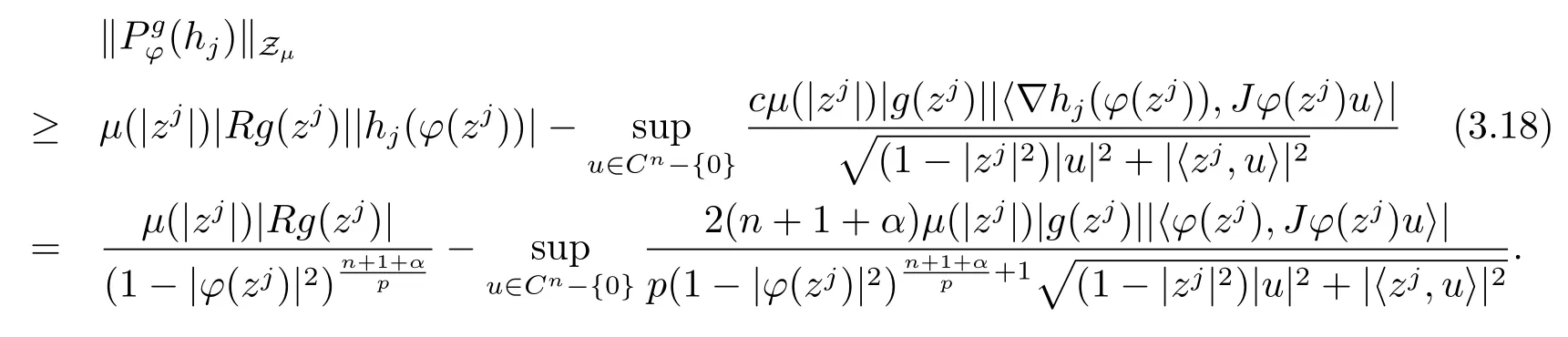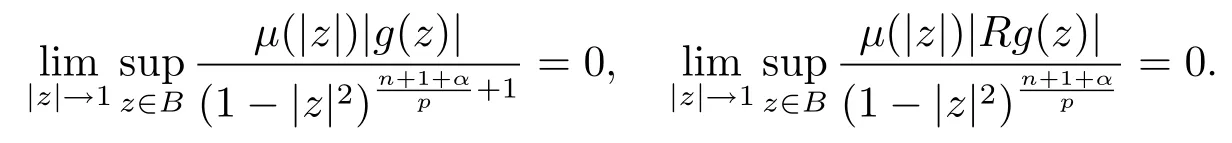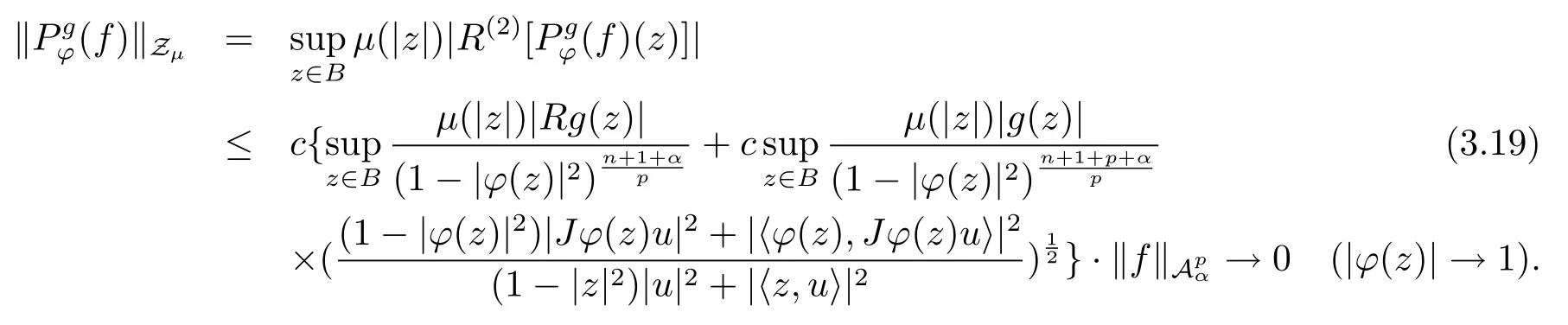單位球上加權(quán)Bergman空間到Zygmund型空間上的積分型算子
趙艷輝, 廖春艷, 鄧春紅
(1.湖南科技學(xué)院理學(xué)院, 湖南永州 425199)
(2.湖南科技學(xué)院理學(xué)院計(jì)算數(shù)學(xué)研究所, 湖南永州 425199)
1 引言
設(shè)B表示Cn上的單位球,?B 表示單位球面,dv為標(biāo)準(zhǔn)體測(cè)度, 滿足v(B) = 1,dσ為標(biāo)準(zhǔn)面測(cè)度, 滿足σ(?B)=1,H(B) 代表B上的全純函數(shù)類.
定義1.1設(shè)0

表示B上的加權(quán) Bergman 空間其中
當(dāng) 1≤p<∞時(shí),在范數(shù)下是一個(gè) Banach 空間.當(dāng) 0 定義1.2設(shè)[0,1) 上的連續(xù)函數(shù)μ(r)>0, 如果存在常數(shù)0 設(shè)μ為[0,1) 上的正規(guī)函數(shù),f ∈H(B), 這里?f表示f的復(fù)梯度,由文獻(xiàn) [1]知等價(jià). 設(shè)μ為 [0,1) 上的正規(guī)函數(shù), 稱f屬于βμ空間是指:空間在范數(shù) 下是一個(gè)Banach 空間. 由文獻(xiàn) [2]中的引理 2.1 可知, 設(shè)μ為 [0,1) 上的正規(guī)函數(shù), 稱f ∈βμ當(dāng)且僅當(dāng) 定義1.3設(shè)μ為[0,1) 上的正規(guī)函數(shù),B上的全純函數(shù)f如果滿足 則稱f屬于Zygmund 型空間則稱f屬于小 Zygmund 型空間(見文獻(xiàn) [3–5]).如果μ(r)=1?r2, Zygmund 型空間(小 Zygmund 型空間就是典型的Zygmund 空間Z(小Zygmund 空間), 這里R(2)f(z)=R(Rf(z)). 定義1.4設(shè)?是B上的全純自映射,g ∈H(B) 且g(0)=0, 則由?和g誘導(dǎo)的H(B)上的算子定義為 文獻(xiàn)[3–11]研究了該類算子的性質(zhì).若用Rg代替g, 且?(z) =z, 算子Pg就是加權(quán)算子, 它在文獻(xiàn)[12]被引入并研究, 文獻(xiàn)[13–16]對(duì)幾個(gè)全純函數(shù)空間上的加權(quán)算子的有界性和緊性進(jìn)行了討論.關(guān)于Bergman 空間上的復(fù)合算子和算子的有界性和緊性問題的討論得到了一些很好的結(jié)論, 如文獻(xiàn)[1,2,16–18]. 本文的主要工作就是在Cn中的單位球上來給出空間到型空間上的有界算子和緊算子的充要條件.同時(shí)分別得到了單位圓盤D上和?(z) =z時(shí)單位球上的相應(yīng)結(jié)論.本文中用記號(hào)c,c1,c2來表示與變量z,ω?zé)o關(guān)的正數(shù),c,c1,c2可以與某些范數(shù)或有界量有關(guān), 不同的地方可以表示不同的正常數(shù). 引理2.1[7]設(shè)f,g ∈H(B),g(0)=0, 則 引理 2.2[2]設(shè)則 引理2.3設(shè)0 證由引理2.2 和Montel 定理按定義可證. 引理2.4[3]中的閉子集K是緊子集的充要條件是K是有界集, 且滿足 定理3.1設(shè)0 這里J?(z) 是?(z) 的 Jacobi 矩陣, 且 證 充分性設(shè)(3.1) – (3.2) 成立, 則由和引理2.1–2.2 有 必要性設(shè)空間到Zμ型空間的有界算子.取則由和βμ的定義可知g ∈βμ,g?l ∈βμ(l=1,2,···,n). (1) 先證 (3.1) 式成立.?ω ∈B,u ∈Cn ?{0}. 則fω(?(ω))=0, 且由文獻(xiàn) [19]中的定理 1.12 有 則fω(?(ω))=0, 且由文獻(xiàn) [20]中的命題 1.4.10 有 所以類似(3.5) 式的證明, 結(jié)合(3.6) 式有 下面證明(3.2) 式成立.取 所以(3.2) 式成立. 綜上所述, 定理3.1 得證. 當(dāng)?(z)=z時(shí), 易知下列結(jié)論成立. 推論 3.2設(shè) 0 而對(duì)于單位圓盤則有以下結(jié)論成立. 推論 3.3設(shè) 0 定理3.4設(shè)0 證 充分性假設(shè)(3.8)和(3.9)式成立,則對(duì)任意ε>0,存在0<δ<1,當(dāng)|?(z)|2>1?δ時(shí), 設(shè){fj} 是在B的任一緊子集上一致收斂于0 并滿足的全純函數(shù)列, 則 {fj}和 {?fj} 在E={ω:|ω|2≤1?δ} 上一致收斂于 0. 若 |?(z)|2>1?δ, 由 (3.10)–(3.11) 式及引理 2.2, 有 若|?(z)|2≤1?δ,因?yàn)間 ∈βμ,g?l ∈βμ,所以由{fj} 和{?fj} 在E={ω:|ω|2≤1?δ}上一致收斂于0, 有 注意到{g(0)fj(?(0))}一致收斂于0,結(jié)合(3.12)式和(3.13)式,有0, 從而根據(jù)引理2.3 知空間到Zμ型空間的緊算子. 必要性設(shè)空間到Zμ型空間的緊算子, 由有界性的證明知g ∈ βμ,g?l ∈ βμ. 假設(shè) (3.8) 式不成立, 則存在 {zj}?B,{uj}?Cn ?{0} 和常數(shù)ε0> 0, 使得rj=|?(zj)|→1(j →∞), 有 則fj(?(zj))=0.類似定理 3.1 中的證明易知 下面證明{fj} 在B的任一緊子集E ?{z:|z|≤r},0 所以{fj} 在B的任一緊子集上一致趨于0.但由(3.14) 式, 類似定理3.1 中的證明有 則fj(?(zj)) = 0.經(jīng)計(jì)算易知且 {fj} 在B的任一緊子集E ?{z:|z|≤r},0 下面證明(3.9) 式成立.假設(shè)(3.9) 式不成立, 則存在{zj}?B和常數(shù)ε0> 0, 使得|?(zj)|→1(j →∞), 有 當(dāng)?(z)=z時(shí), 易知下列結(jié)論成立. 推論 3.5設(shè) 0 而對(duì)于單位圓盤則有以下結(jié)論成立. 推論 3.6設(shè) 0 定理 3.7設(shè) 0 證因?yàn)榫o算子是有界算子, 所以(1)?(2) 成立, 由空間的定義及定理3.4 知(2)?(3) 也成立.再證 (3)?(1), 先證 (3)?(2).由定理 3.4, 對(duì)任意的類似于定理3.1 中充分性的證明有 再證(3)?(1).若條件(3) 成立, 則條件(2) 成立.集合在空間中是有界的, 由定理3.4 并結(jié)合(3.19) 式有
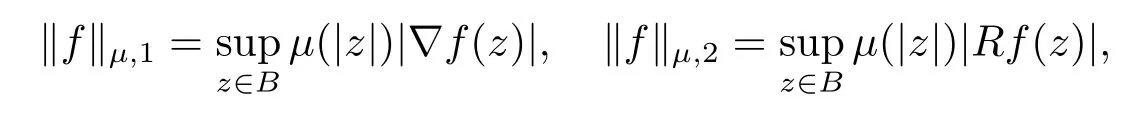

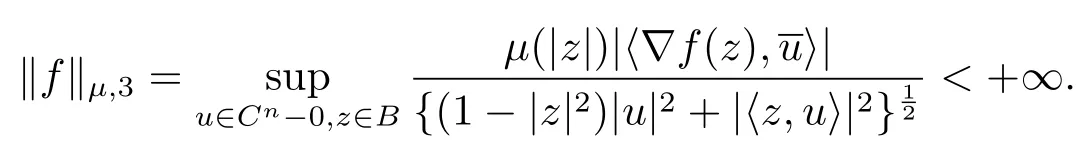
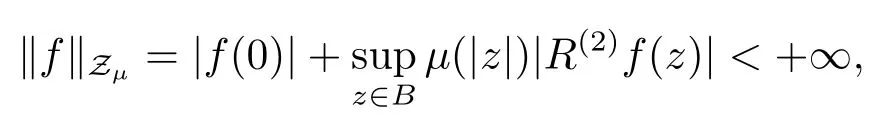
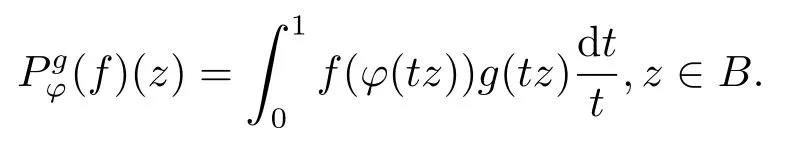
2 有關(guān)引理

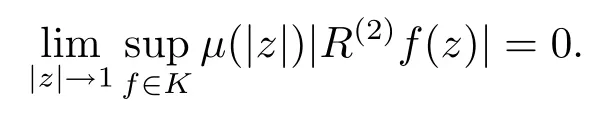
3 主要結(jié)果