李遠飛,郭戰(zhàn)偉

(廣東財經(jīng)大學華商學院應(yīng)用數(shù)學系,廣東 廣州 511300)

1 引言

在本文中,假設(shè)?是R3上的光滑有界區(qū)域,而且在該區(qū)域上存在兩種不同的流體.他們存在的區(qū)域分別為 ?1和 ?2,?=?1∪?2.?1和?2的交界面位于平面x3=0上,其中?1和?2分別位于x3=0的上方和下方,把交界面記為L.共振滲透對流的流體存在于區(qū)域?1上,其控制方程為Brinkman方程,在?2上存在一個多孔介質(zhì)流體,滿足Darcy方程.記??1和??2分別為?1和?2的光滑的邊界.邊界除了公共界面L外的部分分別記為Γ1和Γ2.顯然,??1=Γ1∪L和??2=Γ2∪L.

令(ui,T,p)和(vi,θ,q)分別表示流體在區(qū)域?1和?2上的速度、溫度和壓強.研究的Brinkman方程為

其中g(shù)i是重力函數(shù),不失一般性假設(shè)maxgigi≤1,Q(x,t)是內(nèi)部的熱源或一個散熱器.研究已經(jīng)表明,對于此問題,當考慮平面無限層中的熱對流時,內(nèi)層之間可能出現(xiàn)共振.一個關(guān)鍵參數(shù)是內(nèi)部熱源,它的存在可能導致振蕩不穩(wěn)定.因此,研究各種類型的偏微分方程控制的多孔介質(zhì)非等溫流動模型在一般三維區(qū)域內(nèi)對熱源本身連續(xù)依賴性是具有實際意義的,有興趣的讀者參看文獻[1-5].值得一提的是文獻[1]以及其中引用的許多參考文獻講述了物理相關(guān)問題的很多應(yīng)用.區(qū)域?2上Darcy方程為(見文獻[6])

其中τ是一個給定的常數(shù)滿足0≤τ<∞.假設(shè)流體處于一個外界溫度為Ta的環(huán)境中,在區(qū)域的邊界上滿足牛頓冷卻定律.因此問題的邊界條件可以寫為

其中k1和k2是牛頓冷卻定律中的冷卻系數(shù),是區(qū)域??2的單位外法向量.并且記是區(qū)域??1的單位外法向量.顯然.初始條件為

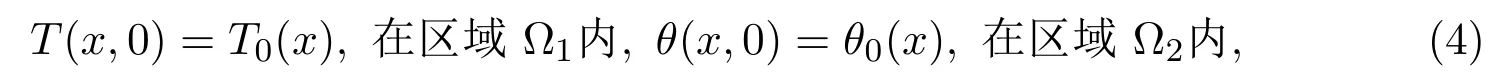
其中T0和θ0是給定的函數(shù).在交界面L上的條件為

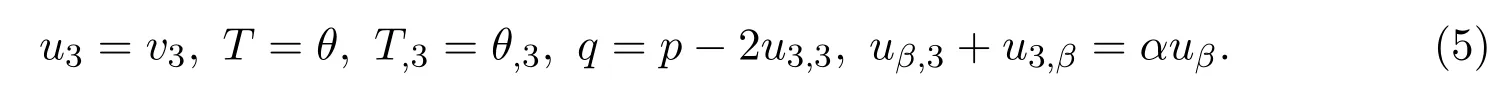
其中α是由給定流體和給定多孔固體通過實驗確定的系數(shù).這些邊界條件在文獻[6]中得到了詳細討論.(5)式中的最后一個條件實質(zhì)上是從文獻[7]中得出的.文獻[8]在實驗結(jié)果的基礎(chǔ)上進行了論證.在第二部分將推導溫度的先驗界.利用這些先驗界,在第三部分證明熱源和冷卻系數(shù)的連續(xù)依賴性.

2 先驗界

3 主要定理及其證明

3.1 對熱源的連續(xù)依賴性

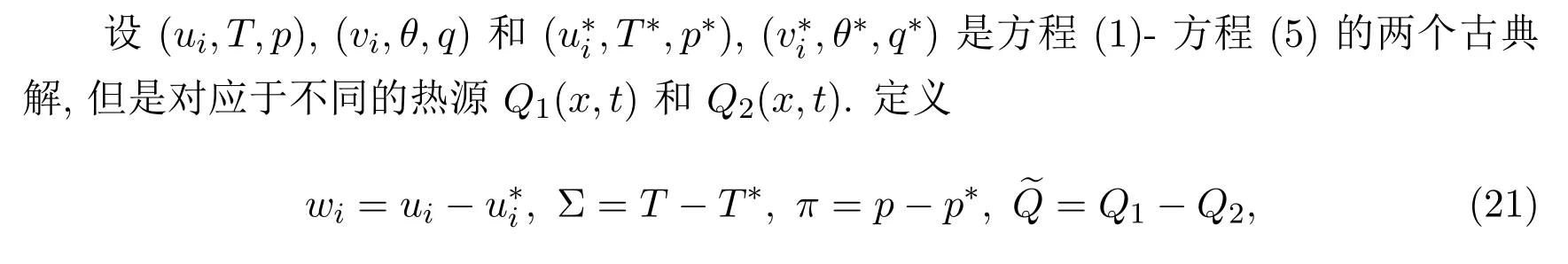
3.2 牛頓冷卻定律中冷卻系數(shù)的連續(xù)依賴性