GUAN Jin-rui, ZHOU Fang, ZUBAIR Ahmed

(1.Department of Mathematics, Taiyuan Normal University, Jinzhong 030619, China)

(2.Institute of Mathematics and Computer Science, University of Sindh, Jamshoro, Pakistan)

Abstract: In this paper, we study the numerical solution of M-matrix algebraic Riccati equation.Based on the alternately linearized implicit iteration method, we propose a modified alternately linearized implicit iteration method (MALI) for computing the minimal nonnegative solution of MARE.Convergence of the MALI iteration method is proved under suitable conditions.Convergence rate with optimal parameters are given for the MARE associated with a nonsingular M-matrix or an irreducible singular M-matrix.Numerical experiments are given to show that the MALI iteration method is feasible in some cases.

Keywords: algebraic Riccati equations; minimal nonnegative solution; M-matrix; ALI iteration method

1 Introduction

We study M-matrix algebraic Riccati equation (MARE) of the form

whereA,B,C,Dare real matrices of sizesm×m,m×n,n×m,n×n, respectively, and

is an M-matrix.M-matrix algebraic Riccati equation arises from many branches of applied mathematics,such as transport theory,Wiener-Hopf factorization of Markov chains,stochastic process, and so on [1–5].Research on the theories and the efficient numerical methods of MARE became a hot topic in recent years [6–19].

The following are some notations and definitions we will use later.

For any matricesA=(aij),B=(bij) ∈Rm×n, we writeA≥B(A>B), ifaij≥bij(aij>bij) for alli,j.Ais called a Z-matrix ifaij≤0 for allZ-matrixAis called an M-matrix if there exists a nonnegative matrixBsuch thatA=sI?Bands≥ρ(B),whereρ(B) is the spectral radius ofB.In particular,Ais called a nonsingular M-matrix ifs>ρ(B) and singular M-matrix ifs=ρ(B).

We first review some basic results of M-matrix.The following lemmas can be found in[20, Chapter 6].

Lemma 1.1(see[20]) LetAbe a Z-matrix,then the following statements are equivalent

(1)Ais a nonsingular M-matrix;

(2)A?1≥0;

(3)Av>0 for some vectorsv>0;

(4) all eigenvalues ofAhave positive real part.

Lemma 1.2(see [20]) LetA,Bbe Z-matrices.IfAis a nonsingular M-matrix andA≤B, thenBis also a nonsingular M-matrix.In particular, for any nonnegative real numberα,B=αI+Ais a nonsingular M-matrix.

Lemma 1.3(see [20]) LetAbe an M-matrix,B≥Aa Z-matrices.IfAis nonsingular or ifAis singular and irreducible withthenBis also a nonsingular M-matrix.

Lemma 1.4(see [20]) LetAbe a nonsingular M-matrix or an irreducible singular M-matrix.Ais partitioned as

whereA11andA22are square matrices, thenA11andA22are nonsingular M-matrices.

Lemma 1.5(see [20]) LetA,Bbe nonsingular M-matrices andA≤B, thenA?1≥B?1.

Lemma 1.6(see [13]) LetAbe an M-matrix andλmin(A) be the eigenvalue ofAwith smallest absolute value.Thenλmin(A) is nonnegative and satisfies

For the minimal nonnegative solution of the MARE, we have the following important result.

Lemma 1.7(see [3, 5, 6]) IfKin (1.2) is a nonsingular M-matrix or an irreducible singular M-matrix, then (1.1) has a minimal nonnegative solutionS.IfKis a nonsingular M-matrix, thenA?SCandD?CSare also nonsingular M-matrices.IfKis irreducible M-matrix, thenS>0 andA?SCandD?CSare also irreducible M-matrices.

Lemma 1.8(see [3, 5]) IfKin (1.2) is an irreducible singular M-matrix, then there exist unique, up to a multiplicative constant,u>0 andv>0 such thatuTK=0,Kv=0 anduTv=1.

Partition the vectorsuandvin the above lemma according to the block structure of the matrixKasthroughuandvwe can define the driftμas the real number

The term ”drift” originates in the context of Markov chains and describes the different physical behaviors of the chain in the cases whereμis positive, null, or negative.In this context the terms positive recurrent, null recurrent, and transient are used to denote the caessμ<0,μ=0, andμ>0, respectively.

In terms of the definition, we have the following result.

Lemma 1.9(see [3]) IfKdefined in (1.2) is an irreducible singular M-matrix andSis the minimal nonnegative solution of the MARE (1.1).Then

(i) whenμ<0,D?CSis singular andA?SCis nonsingular;

(ii) whenμ>0,D?CSis nonsingular andA?SCis singular;

(iii) whenμ=0, bothD?CSandA?SCare singular.

Efficient numerical methods for MARE include fixed-point iterative methods, Newton method, SDA, and so on.For details see [3, 5, 8, 9, 11, 13].

Recently,Bai et al.[8]proposed an alternately linearized implicit iteration method(ALI)for the MARE,which is very simple and efficient than the fixed-point iterative methods and Newton method,since at each iteration only two linear matrix equations are needed to solve.

The ALI iteration method

?SetX0=0 ∈Rm×n.

?Fork=0,1,···, until {Xk} converge, computeXk+1fromXkby solving the following two systems of linear matrix equations

whereα>0 is a given parameter.

However, there still has room to improve the ALI iteration method.In this paper, to fully improve the effectiveness of the ALI iteration method,we propose a modified alternately linearized implicit iteration method(MALI)which has two parameters and includes the ALI iteration method as special cases.

The rest of this paper is organized as follows.In next section, we propose a modified alternately linearized implicit iteration method and give its convergence analysis.In Section 3, we analysis the convergence rate and the optimal parameters of the MALI iteration method.In Section 4, we use some numerical examples to show the feasibility of the MALI iteration method.Conclusion is given in the last section.

2 The MALI Iteration Method

In the following,we propose a modified alternately linearized implicit iteration method.

The MALI iteration method

?SetX0=0 ∈Rm×n.

?Fork=0,1,···, until {Xk} converge, computeXk+1fromXkby solving the following two systems of linear matrix equations

whereα>0,β>0 are two given parameters.

Compared with the ALI iteration method, there are two parametersαandβin the MALI iteration method, which will reduce to the ALI iteration method whenα=β.Hence the ALI iteration method is a special case of the MALI iteration method.

In the following, we give convergence analysis of the MALI iteration method.First we need several lemmas.

Lemma 2.1Let{Xk}be the matrix sequence generated by the MALI iteration method,R(X)=XCX?XD?AX+B, andSbe the minimal nonnegative solution to (1.1).Then for anyk≥0, the following equalities hold

(1) (Xk+1/2?S)(αI+(D?CXk))=(αI?(A?SC))(Xk?S);

(2) (Xk+1/2?Xk)(αI+(D?CXk))=R(Xk);

(3)R(Xk+1/2)=(αI?(A?Xk+1/2C))(Xk+1/2?Xk);

(4) (βI+(A?Xk+1/2C))(Xk+1?S)=(Xk+1/2?S)(βI?(D?CS));

(5) (βI+(A?Xk+1/2C))(Xk+1?Xk+1/2)=R(Xk+1/2);

(6)R(Xk+1)=(Xk+1?Xk+1/2)(βI?(D?CXk+1)).

ProofThe proof is similar to that of in [8], so we omit here.

Lemma 2.2For the MARE (1.1), if the matrixKin (1.2) is a nonsingular M-matrix or an irreducible singular M-matrix,Sis the minimal nonnegative solution to(1.1), then for anyδ> 0 and 0≤Z≤S, the matricesδI+A?ZCandδI+D?CZare nonsingular M-matrices.

ProofFirst, from 0≤Z≤S, we haveA?SC≤A?ZCandD?CS≤D?CZ.

IfKis a nonsingular M-matrix, thenA?SCandD?CSare also nonsingular M-matrices by Lemma 1.7.ThusδI+A?ZCandδI+D?CZare nonsingular M-matrices by Lemma 1.2.

IfKis an irreducible M-matrix,thenA?SCandD?CSare also irreducible M-matrices by Lemma 1.7.Sinceδ> 0,By Lemma 1.3,δI+A?ZCandδI+D?CZare nonsingular M-matrices.

Lemma 2.3For the MARE (1.1), suppose that the matrixKin (1.2) is a nonsingular M-matrix or an irreducible singular M-matrix,Sis the minimal nonnegative solution to(1.1), and the parametersα,βsatisfy

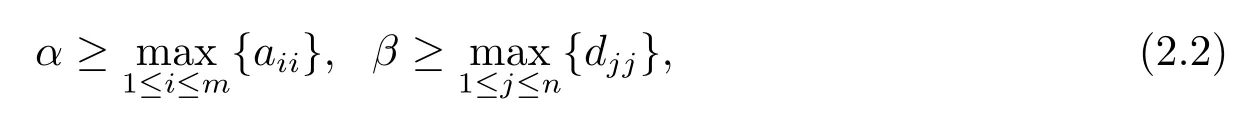
whereai,ianddj,jare diagonal entries ofAandD, respectively, then for anyk≥0,

(i) {Xk+1/2} and {Xk+1} are well defined and bounded

(ii)βI+A?Xk+1/2CandαI+D?CXk+1are nonsingular M-matrices.

ProofIfKis a nonsingular M-matrix or an irreducible singular M-matrix, from Lemma 1.4,AandDare nonsingular M-matrices.Thus, whenαandβsatisfy (2.2), bothαI?AandβI?Dare nonnegative matrices.

We prove this lemma by induction.Whenk=0, we haveX1/2(αI+D)=BsinceX0=0 from the MALI iteration.AsDis a nonsingular M-matrix, by Lemma 1.2,αI+Dis also a nonsingular M-matrix.Thus from Lemma 1.1 we have (αI+D)?1≥0.Hence

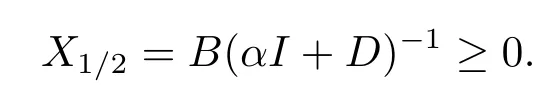
On the other hand, from Lemma 2.1(1), we have

Thus sinceC≥0 andS≥0, we have

This show that 0≤X1/2≤S.

On the other hand, sinceC≥0, we haveA?SC≤A?X1/2C.Since thatDis a nonsingular M-matrix,βmust be positive from(2.2).ThusβI+A?X1/2Cis a nonsingular M-matrix by Lemma 2.2.

Similarly, from the MALI iteration and Lemma 2.1(4), we have

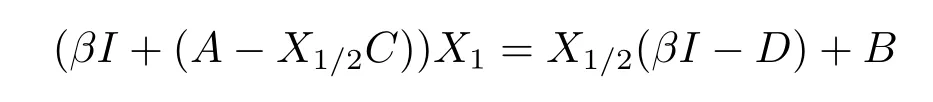
and

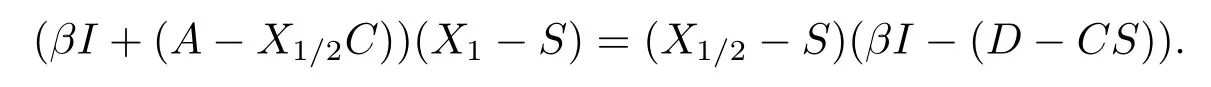
Hence

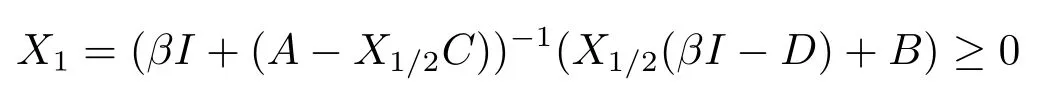
and

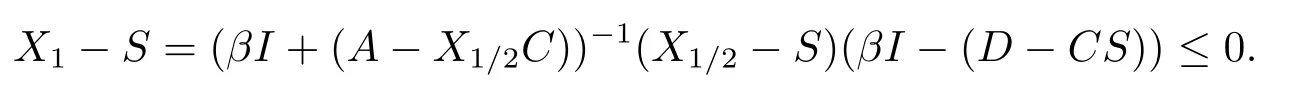
This show that 0≤X1≤S.

On the other hand, sinceC≥0, we haveD?CS≤D?CX1.Note thatAis a nonsingular M-matrix,αmust be positive.By Lemma 2.2,αI+D?CX1is a nonsingular M-matrix.

Thus (i) and (ii) hold true fork=0.

Assume that (i) and (ii) hold true fork=l?1.From the MALI iteration, we have

thus

From Lemma 2.1(1), we have (Xl+1/2?S)(αI+(D?CXl))=(αI?(A?SC))(Xl?S),thus

This show that 0≤Xl+1/2≤S.

Again, sinceC≥0 andβ> 0, by Lemma 2.2,βI+A?Xl+1/2Cis a nonsingular M-matrix.

Similarly, from the MALI iteration and Lemma 2.1(4), we have

and

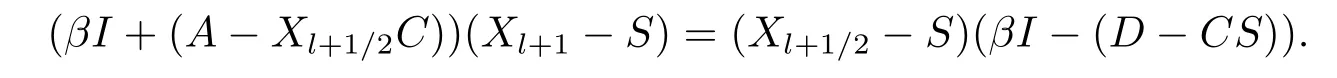
Hence

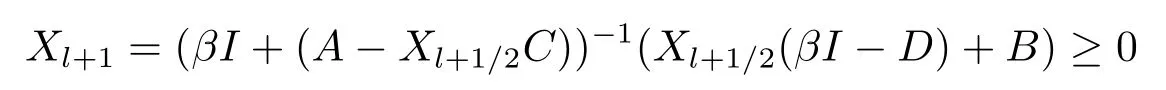
and

This show that 0≤Xl+1≤S.

Again, sinceC≥0 andα> 0, by Lemma 2.2,αI+D?CXl+1is a nonsingular M-matrix.

Thus we prove by induction that (i) and (ii) hold true for allk≥0.

Lemma 2.4Under the assumption of Lemma 2.2, the following inequalities hold for allk≥0,

whereR(X) is defined in Lemma 2.1.

ProofWe prove this lemma by induction.

In fact, whenk=0, we haveR(X0)=B≥0.From Lemma 2.1(2), we have

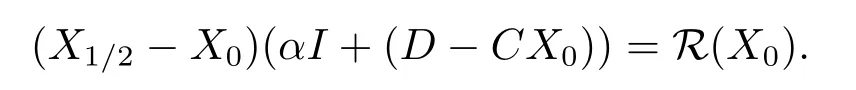
SinceαI+Dis a nonsingular M-matrix,

From Lemma 2.1(3), we have

From Lemma 2.1(5), we have (βI+(A?X1/2C))(X1?X1/2)=R(X1/2).By Lemma 2.2,βI+(A?X1/2C) is a nonsingular M-matrix, we have

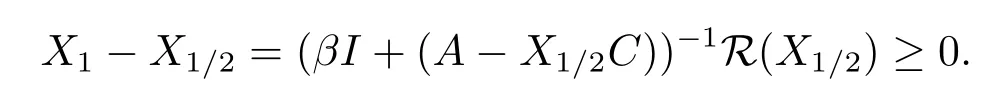
From Lemma 2.1(6), we have

This show that (2.4) holds fork=0.

Now we suppose that (2.4) holds fork=l?1.Then from Lemma 2.1(2) and Lemma 2.2, we have

From Lemma 2.1(3), we have

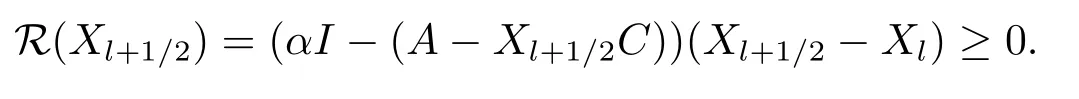
From Lemma 2.1(5) and Lemma 2.2, we have

From Lemma 2.1(6), we have

Thus we show by induction that (2.4) holds for allk≥0.

By Lemmas 2.3 and 2.4, we can prove the following convergence theorem of the MALI iteration method.

Theorem 2.1For the MARE (1.1), ifKin (1.2) is a nonsingular M-matrix or an irreducible singular M-matrix,Sis the minimal nonnegative solution to (1.1), and the parametersα,βsatisfy(2.2),then{Xk}is well defined,monotonically increasing and converges toS.

ProofCombining Lemma 2.3 with Lemma 2.4, we show that {Xk} is nonnegative,monotonically increasing and bounded from above.Thus there is a nonnegative matrixS?such thatIt also holds thatFrom Lemma 2.3, we haveS?≤S.On the other hand, take the limit in the MALI iteration, we have thatS?is a solution of the MARE, thusS≤S?.HenceS=S?.

3 Convergence Rate of the MALI Iteration Method

In this section, we analyse the convergence rate and give optimal parameters of the MALI iteration method.

Theorem 3.1Under the assumption of Theorem 2.1,for the sequence{Xk}generated by the MALI iteration method, we have

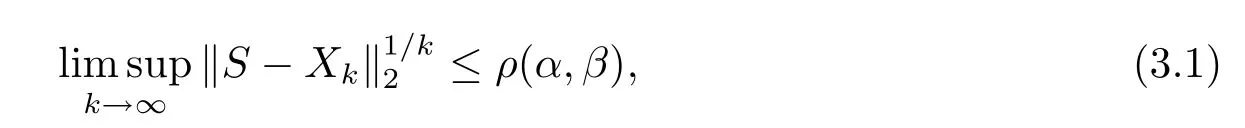
where

and

ProofFrom Lemma 2.1(1) and (4), we have

and

Thus

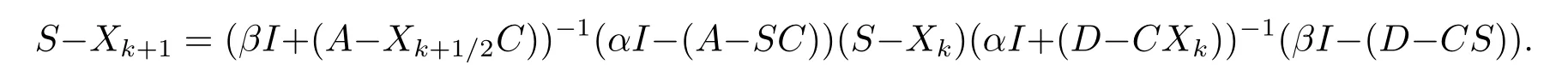
BecauseβI+(A?SC)≤βI+(A?Xk+1/2C), by Lemma 1.5, we have

Similarly, we have

Thus

By induction we have

Hence

Take limit on both side and, note thatwe have

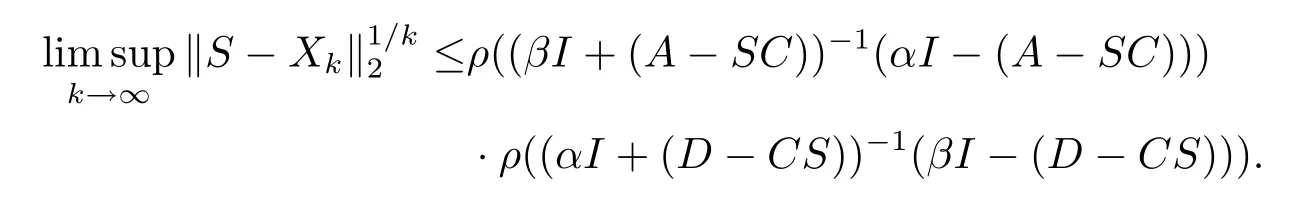
It’s easy to verify that

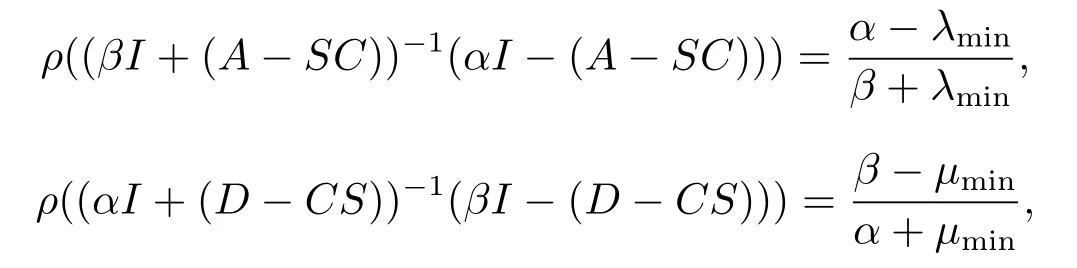
whereλmin=λmin(A?SC) andμmin=μmin(D?CS).Hence

Corollary 3.1WhenKin (1.2) is a nonsingular M-matrix or an irreducible singular M-matrix with nonzero drift, for anyα,βsatisfy (2.2), we haveρ(α,β) < 1.In this case,the MALI iteration method has linear convergence rate.WhenKis an irreducible singular M-matrix with zero drift, for anyα,βsatisfy (2.2), we haveρ(α,β)=1.In this case, the the MALI iteration method has sub-linear convergence rate.

ProofWhenKis a nonsingular or an irreducible singular M-matrix with nonzero drift, we know thatA?SCandD?CShave at least one which is nonsingular by Lemma 1.9.By Lemma 1.6,

where (A?SC)iiis the diagonal entries ofA?SCand (D?CS)iiis the diagonal entries ofD?CS.Thusρ(α,β)<1.In this case, the MALI iteration method has linear convergence rate.

WhenKis an irreducible singular M-matrix with zero drift,we know that bothA?SCandD?CSare singular M-matrices by Lemma 1.9.Thusλmin(A?SC)=0,μmin(D?CS)=0.Henceρ(α,β)=1.In this case,the the MALI iteration method has sub-linear convergence rate.

Corollary 3.2The optimal parameters of the MALI iteration method are

ProofIt’s easy to verify thatρ(α,β) is an increasing function with respect toα,β.Thus the minimum ofρ(α,β) is attained atα=max{aii},β=max{djj}.

Note that, in Corollary 3.2, the optimal parameters only minimize the upper bound of the contraction factor.

4 Numerical Experiments

In this section we use several examples to show the feasibility of the MALI iteration method.We compare the MALI iteration method with the ALI iteration method in [8],Newton method in [3, 11]and present computational results in terms of the numbers of iterations (IT), CPU time (CPU) in seconds and the residue (RES), where

In our implementations all iterations are performed in MATLAB (version 2012a) on a personal computer and are terminated when the current iterate satisfiesRES< 10?6or the number of iterations is more than 9000, which will be denoted by ’-’.

Example 1Consider the MARE (1.1) with

whereEm×nis them×nmatrix with all ones andImis the identity matrix of sizemwithm=2,n=18.This example is from [5], where the correspondingKis an irreducible singular M-matrix.The computational results are summarized in Table 1.

Table 1 Numerical Results of Example 1

Example 2Consider the MARE (1.1) with

This example is taken from [5], where we chooseα=2 and the correspondingKis an irreducible singular M-matrix withμ> 0.The computational results are summarized in Table 2 for different sizes ofn.

From the two numerical experiments, we can observe that the MALI iteration method needs the least CPU time than the ALI iteration method and Newton method.So it is feasible.

Table 2 Numerical Results of Example 2

5 Conclusions

We propose a modified alternately linearized implicit iteration method(MALI)for computing the the minimal nonnegative solution of MARE.Theoretical analysis and numerical experiments show that the MALI iteration method is feasible in some cases.However, since the MALI iteration method only has linear convergence rate in general,it will be very slowly as compared with the SDA algorithm in [9, 15].So, in general, the SDA algorithm will be more preferable.