時(shí)標(biāo)上具有分布勢函數(shù)的Sturm-Liouville問題的矩陣表示
劉娜娜,敖繼軍
( 內(nèi)蒙古工業(yè)大學(xué)理學(xué)院,內(nèi)蒙古 呼和浩特010051)
1.引言
近年來,關(guān)于Sturm-Liouville(S-L)問題的特征值問題已經(jīng)成為數(shù)學(xué)物理等領(lǐng)域研究的熱門課題,并取得了許多成果[1].早在1964年,Atkinson提出了二階S-L問題在某些條件下存在有限譜的論斷[2].2001年KONG,WU和Zettl運(yùn)用構(gòu)造的方法證實(shí)了Atkinson論斷的合理性[3].由此學(xué)者們對有限譜問題展開了一系列研究.2009年KONG,Volkmer,Zettl分別在分離型和實(shí)耦合型自共軛邊界條件下研究了具有有限譜的S-L問題的矩陣表示[4].2011年,AO,SUN,ZHANG討論了帶有轉(zhuǎn)移條件的S-L問題的有限譜[5].2017年,敖繼軍,薄芳珍給出了帶譜參數(shù)邊界條件的四階邊值問題的矩陣表示的結(jié)論[6].
為了找到一種能夠?qū)㈦x散和連續(xù)兩者結(jié)合起來,將微分方程和差分方程結(jié)合起來的理論框架,1988年,德國數(shù)學(xué)家Stefan Hilger在他的博士論文中首次提出了時(shí)標(biāo)的概念.所謂時(shí)標(biāo)(測度鏈)就是指實(shí)數(shù)集R的任一非空閉子集,它可以把連續(xù)理論和離散理論融合在一起研究.如今,時(shí)標(biāo)理論已經(jīng)基本完善,許多學(xué)者對時(shí)標(biāo)上的S-L問題從多個(gè)方面進(jìn)行了一系列研究[7?12].1999年,Agarwal等在文[7]中討論了p=1時(shí)二階S-L問題在分離型邊界條件下特征值的存在性以及特征值廣義零點(diǎn)的個(gè)數(shù).隨后KONG將他們的結(jié)論推廣到了分離型邊界條件下一般的S-L問題上,并討論了特征值的依賴性[8].2010年,XIE 等在文[9]中運(yùn)用不動(dòng)點(diǎn)原理研究了時(shí)標(biāo)上高階微分方程邊值問題正解的存在性.2013年,趙娜在文[10]中考慮了二階S-L問題的有限譜,分別討論了分離型和耦合型S-L問題的有限個(gè)特征值,給出了其特征值不等式,并將結(jié)論推廣到較一般的時(shí)標(biāo)上.2016年,Tuna[11]研究了時(shí)標(biāo)上二階耗散S-L問題的完備性.
從目前的研究現(xiàn)狀可以看出,學(xué)者們在S-L問題的有限譜,S-L問題的矩陣表示,具有分布勢函數(shù)的S-L問題,時(shí)標(biāo)上S-L問題的特征值等問題方面已經(jīng)取得了很多理論成果.文[12]將以上問題進(jìn)行了推廣,討論了時(shí)標(biāo)上具有分布勢函數(shù)且邊界條件帶有譜參數(shù)的S-L問題的有限譜.但是對于時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題的矩陣表示還尚未見有結(jié)論.本文利用文[10]的方法,也是通過分割時(shí)標(biāo)T得到了時(shí)標(biāo)上具有分布勢函數(shù)的二階S-L問題的矩陣表示.
本文考慮時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題與矩陣特征值問題
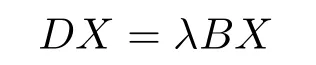
之間的等價(jià)關(guān)系,其中D和B是n ×n復(fù)值矩陣,B是對角矩陣.討論以下具有分布勢函數(shù)的S-L方程[12]:

其中?∞ 考慮邊界條件 且2×4矩陣(A|B)是滿秩的, 本文將自共軛邊界條件(1.3)分為兩種類型來討論: 分離型和實(shí)耦合型.分離型邊界條件為: 實(shí)耦合型邊界條件為: 因y[1]=p[y?+syσ],則方程(1.1)可表示為: 令z=y[1],則方程(1.6)等價(jià)于 從而討論方程(1.1)的矩陣表示問題可轉(zhuǎn)化為討論方程(1.7)的矩陣表示問題. 這部分內(nèi)容將給出本文的主要結(jié)論,首先給出兩個(gè)定義. 定義2.1[13]時(shí)標(biāo)上具有分布勢函數(shù)的S-L方程(1.1)稱為是Atkinson類型的,如果對于任意的正整數(shù)m,n ∈N+,存在對時(shí)標(biāo)T的分割: 使得 以及 定義2.2[4]時(shí)標(biāo)上Atkinson類型的S-L問題稱為是與矩陣特征值問題等價(jià)的,如果它們具有相同的特征值. 接下來再對一些符號進(jìn)行說明,令 對方程(1.7)的解y,z,由條件可知: y在[a2k,a2k+1),k=0,1,...,m上為常數(shù), 現(xiàn)假設(shè) 并令 引理2.1[13]對方程(1.7)的任何一組解y,z有 相反,對于系統(tǒng)(2.7)-(2.13)的任何一組解yk,k=0,1,...,m,zk,k=0,...,m+1和,i=0,1,...,n,,i=0,...,n+1,以及存在方程組(1.7)的唯一解y(t)和z(t)滿足(2.5)和(2.6). 下面說明時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題在邊界條件(1.3)下的矩陣表示,首先討論分離型邊界條件(1.4)的情形. 定理2.1若α ∈[0,π),β ∈(0,π],定義(m+n+3)×(m+n+3)三對角矩陣 及對角矩陣 則時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題(1.1),(1.4)與矩陣特征值問題 推論2.1(i)若α,β ∈(0,π),定義(m+n+3)×(m+n+3)三對角矩陣 及對角矩陣 則時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題(1.1),(1.4)與矩陣特征值問題 (ii) 若α=0,β ∈(0,π),對于矩陣Rαβ,Qαβ,Wαβ也有類似結(jié)論.只是在(2.15),(2.16)中當(dāng)α=0時(shí),sinα=0,y0=0,所以矩陣Rαβ,Qαβ,Wαβ的第一行,第一列在(2.14)中消失,變?yōu)閙+n+2階矩陣,由于sin0,因此在各矩陣最后一行中除以sinβ即可.此時(shí)恰有m+n+2個(gè)特征值. (iii)若α ∈(0,π),β=π,則sinβ=0,=0,所以矩陣Rαβ,Qαβ,Wαβ的最后一行,最后一列在(2.14)中消失,變?yōu)閙+n+2階矩陣,由于sin0,因此在各矩陣第一行中同除以sinα即可.此時(shí)恰有m+n+2個(gè)特征值. (iv)若α=0,β=π,此時(shí)sinα=sinβ=0,且y0==0,所以矩陣Rαβ,Qαβ,Wαβ的第一行,第一列,最后一行,最后一列在(2.14)中消失,變?yōu)閙+n+1階矩陣,此時(shí)恰有m+n+1個(gè)特征值. 以下再來討論實(shí)耦合型邊界條件(1.5)的情形.我們分k12=0和k120兩種情形給出定理. 定理2.2當(dāng)k12=0時(shí),定義(m+n+2)×(m+n+2)矩陣 及對角矩陣 則時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題(1.1),(1.5)與矩陣特征值問題 定理2.3當(dāng)(1.5)中k120時(shí),定義(m+n+3)×(m+n+3)矩陣 及對角矩陣 則時(shí)標(biāo)上具有分布勢函數(shù)的S-L問題(1.1),(1.5)與矩陣特征值問題 若系數(shù)滿足條件(1.2),(2.2)和(2.3),以下結(jié)果說明了具有分布勢函數(shù)的S-L問題(1.1),(1.3)與以分段常值函數(shù)為系數(shù)的S-L問題等價(jià). 定理2.4[13]設(shè)qk,wk,k=0,1,...,m,,,i=0,1,...,n及rk,sk,k=0,1,...,m ?1,,,i=0,1,...,n?1由(2.2),(2.3)給出.定義時(shí)標(biāo)T上的分段常值函數(shù)如下: 當(dāng)sk=0,=0時(shí); 且滿足邊界條件(1.3),則具有分布勢函數(shù)的S-L問題(1.1),(1.3)與以分段常值函數(shù)為系數(shù)的方程和邊界條件(1.3)構(gòu)成的S-L問題具有相同的特征值. 這部分內(nèi)容將給出本文主要定理的證明過程,在證明過程當(dāng)中用到的有關(guān)時(shí)標(biāo)的定義可參見文[10]. 定理2.1的證明由邊界條件(1.4)可知 首先容易得出問題(2.7)-(2.13),(3.1)的解與以下問題的解是一一對應(yīng)的: 事實(shí)上,若假設(shè)yk,k=0,1,2,...,m和zk,k=0,1,2,...,m+1是系統(tǒng)(2.7)-(2.9),(3.1)的解.則(3.2)-(3.4)可由(2.7)-(2.9)得出.同理,(3.6)-(3.8)可由(2.11)-(2.13)通過假設(shè),i=0,1,2,...,n和,i=0,1,2,...,n+1為系統(tǒng)(2.11)-(2.13)的一組解而得到.(3.5)可由(2.10)通過假設(shè),為問題(2.10)的解而得到.其中 另一方面,若設(shè)yk,k=0,1,2,...,m是系統(tǒng)(3.2)-(3.4)的一組解,則z0和zm+1可分別由(3.1),(3.2)和(3.4)定義得出,由(2.7)可定義zk,k=1,2,...,m,然后利用(3.2)-(3.4)進(jìn)行逐步推導(dǎo)即可得(2.8),(2.9),同理可得(2.11)-(2.13).因此由引理2.1,方程(1.7)的任何解,從而也是方程(1.1)的解,被系統(tǒng)(3.1)-(3.8)的解唯一決定.故由(3.1)-(3.8)可得兩類問題之間的等價(jià)性. 定理2.2的證明當(dāng)k12=0時(shí),邊界條件(1.5)可以寫為 其中k11k22=1,即可得到方程組(2.7)-(2.13)與邊界條件(3.9)所構(gòu)成的問題的解與問題(3.2)-(3.8)的解是等價(jià)的,其中方程(3.2)與(3.8)變?yōu)橐韵聝墒? 由(2.7)-(2.9),(3.9)可得: 又因?yàn)閗11k22=1,所以(3.12)可寫作(3.10).剩下的證明過程類似定理2.1的證明過程. 定理2.3的證明當(dāng)時(shí),邊界條件(1.5)可以寫為 其中k11k22?k12k21=1,即定理2.2的證明過程當(dāng)中(3.10),(3.11)式變?yōu)?/p> 剩下的證明過程類似定理2.2的證明,這里就不再重復(fù)了. 該部分內(nèi)容討論矩陣特征值問題 的具有分布勢函數(shù)的S-L問題表示,其中,對稱矩陣D=(dij)是l×l實(shí)三對角矩陣或“幾乎”三對角矩陣,且滿足di,i+10,i=1,2,...,l ?1,對角矩陣B=(bjj)滿足bjj0.由定理2.4可知這種表示并不唯一.接下來利用S-L問題(2.25),(1.3)及其等價(jià)類來描述矩陣問題(4.1)的S-L問題表示,這里僅以分離型邊界條件為例,對于實(shí)耦合型邊界條件情形可用同樣方法得出. 定理4.1設(shè)D是l×l對稱三對角矩陣 其中l(wèi)>3,2≤k ≤l ?2,dij∈R,1≤i,j ≤l,且dj,j+10,j=1,...,l ?1,并設(shè) 1)α,β ∈(0,π),且sk,k=0,...,m ?1,,i=0,...,n ?1 是固定的; 2)α=0,β ∈(0,π),r1,q0,w0與sk,k=0,...,m ?1,,i=0,...,n ?1是固定的; 3)α ∈(0,π),β=π,與sk,k=0,...,m ?1,,i=0,...,n ?1是固定的; 4)α=0,β=π,r1,q0,w0,與sk,k=0,...,m ?1,?si,i=0,...,n ?1是固定的. 在以上任一種情形下,矩陣問題(4.1)的所有S-L問題表示均可以由S-L問題(2.25),(1.4)及其等價(jià)類按照對參數(shù)的任何可能的選取形式給出. 證考慮α,β ∈(0,π)的情形.令m=k ?1,n=l ?k ?2,T=[a,b]∪{c}∪[d,e],?∞ 且 然后,再利用(2.20)-(2.24)在時(shí)標(biāo)T=[a,b]∪{c}∪[d,e]上定義滿足(2.2)-(2.4)的分段常值函數(shù)顯然(4.1)和問題(2.15)具有相同的形式.故由推論2.1可知問題(4.1)和具有分布勢函數(shù)的S-L問題(1.1),(1.4)是等價(jià)的.其它情形證明過程類似. 定理4.2設(shè)D是l×l對稱矩陣 其中l(wèi)>3,2≤k ≤l ?2,dij∈R,1≤i,j ≤l,且dj,j+10,j=1,...,l ?1,d1l0,并設(shè) 1)k120,且sk,k=0,...,m ?1,,i=0,...,n ?1是固定的; 2)k12=0,且q0,w0,sk,k=0,...,m ?1,,i=0,...,n ?1是固定的. 在以上任一種情形下,矩陣問題(4.1)的所有S-L問題表示均可以由S-L問題(2.25),(1.5)及其等價(jià)類按照對參數(shù)的任何可能的選取形式給出. 證考慮k120的情況,將(4.1)乘以(k11d1l)?1,可得矩陣D滿足令m=k ?1,n=l ?k ?2,T=[a,b]∪{c}∪[d,e],?∞< a < b < c < d < e < ∞,根據(jù)(2.1)的一個(gè)分割,可類似定理4.1的方法進(jìn)行證明,與之不同的是 對于k12=0的情形,也可用同樣的方法得到結(jié)論. 注4.1文[13]探究了連續(xù)區(qū)間J=(a,b)上具有分布勢函數(shù)的S-L問題的矩陣表示,而本文是在時(shí)標(biāo)T=[a,b]∪{c}∪[d,e]上討論了具有分布勢函數(shù)的S-L問題的矩陣表示,可將連續(xù)系統(tǒng)與離散系統(tǒng)有效地結(jié)合起來.其中的難點(diǎn)在于要找到離散點(diǎn)和連續(xù)區(qū)間的端點(diǎn)-也就是c點(diǎn)與兩個(gè)連續(xù)區(qū)間[a,b],[d,e]中b點(diǎn)和d點(diǎn)之間的連接矩陣及迭代公式,這也是與連續(xù)區(qū)間上同類問題之間的主要區(qū)別之處.在證明過程中,解決問題的關(guān)鍵是要通過兩個(gè)連接矩陣,找到離散點(diǎn)c點(diǎn)與b點(diǎn),d點(diǎn)之間的連接方程.當(dāng)時(shí)標(biāo)取為區(qū)間時(shí),本文結(jié)論將退化為連續(xù)區(qū)間上具有分布勢函數(shù)的S-L 問題,即文[13]中結(jié)論,進(jìn)一步如果s=0,則本文結(jié)論又可退化為經(jīng)典的S-L問題的矩陣表示問題,即文[4]的結(jié)論.


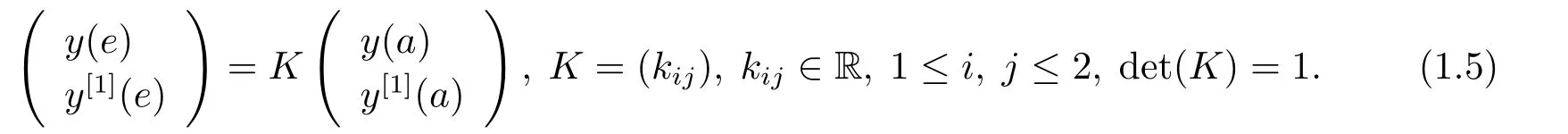

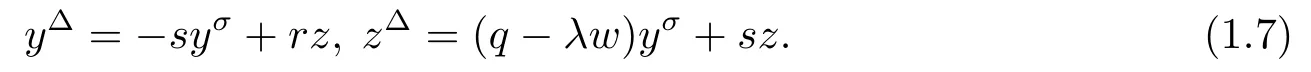
2.主要結(jié)論
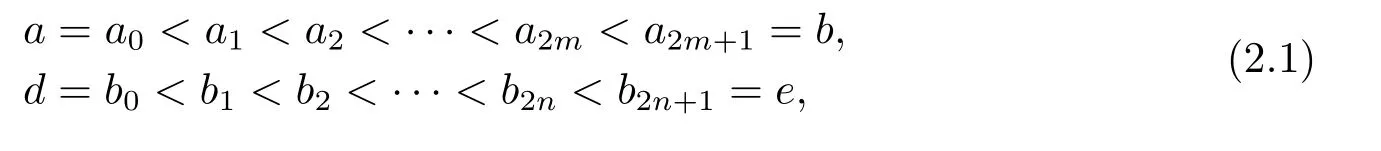


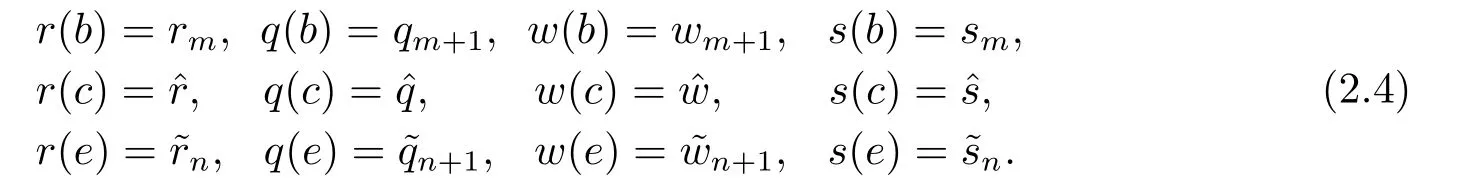





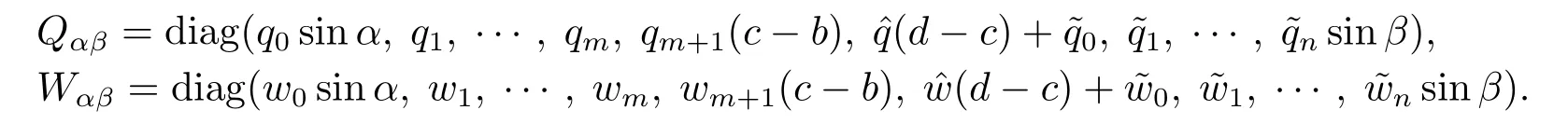

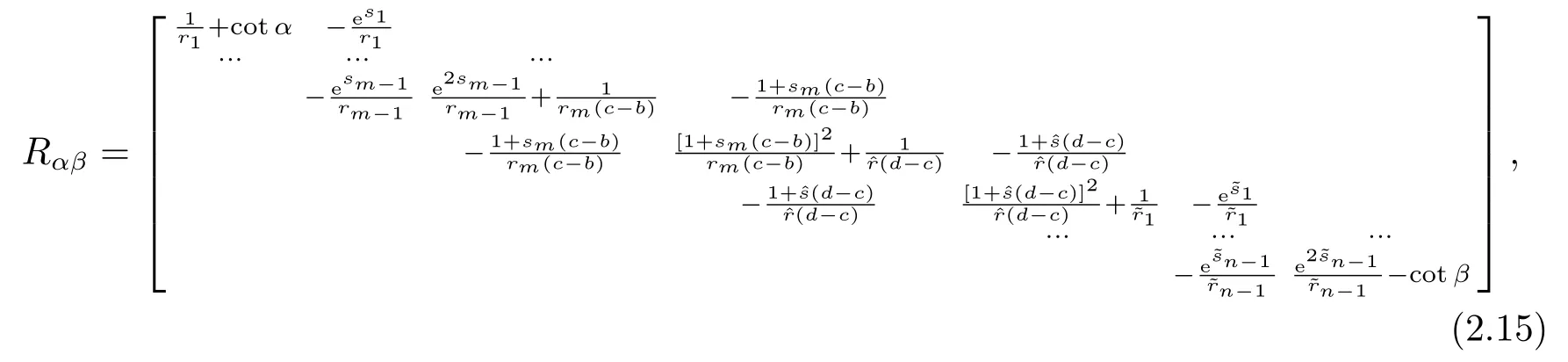


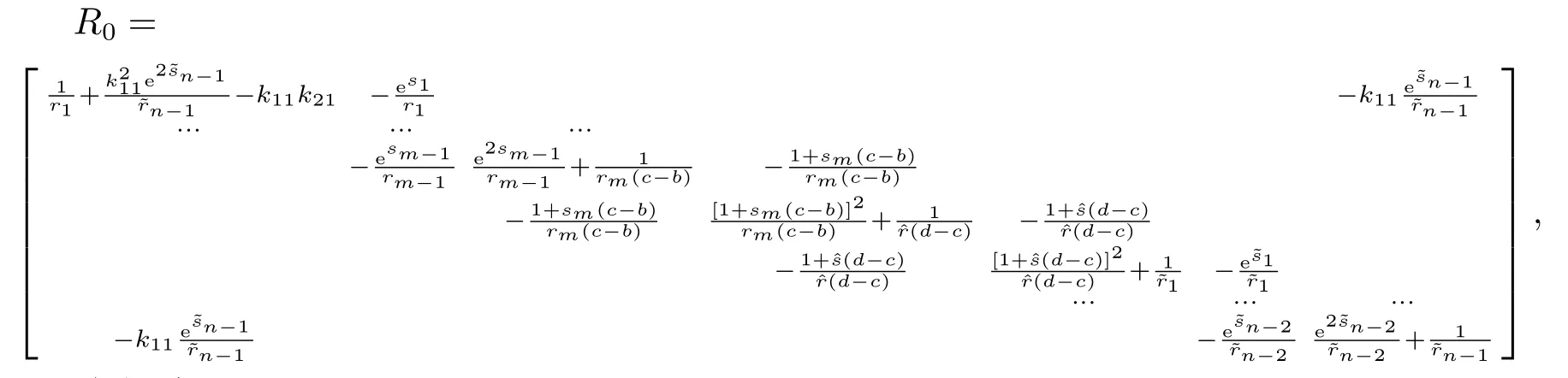
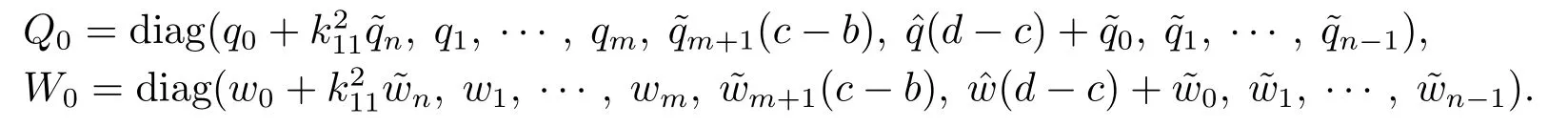

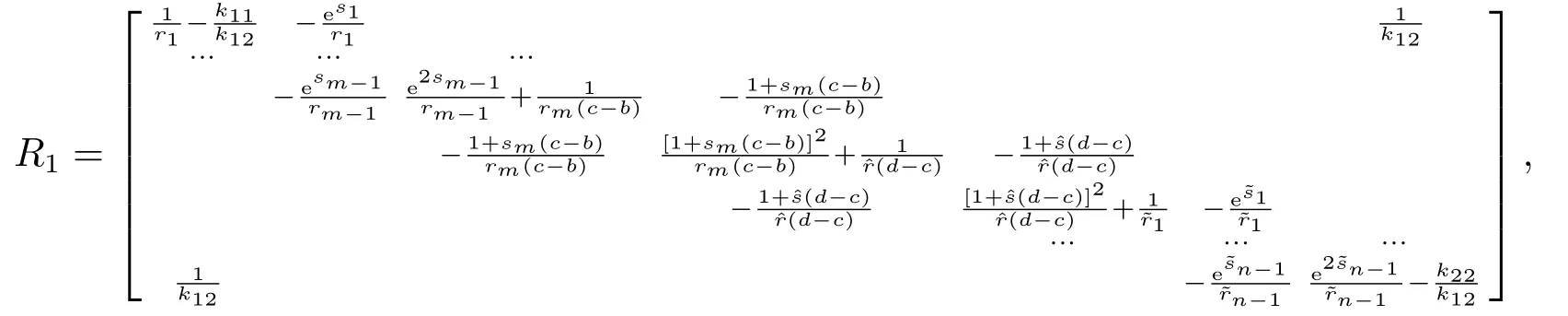
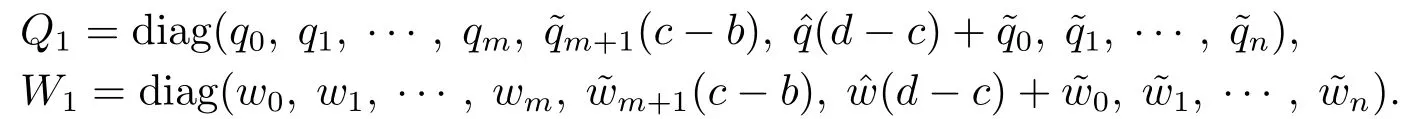


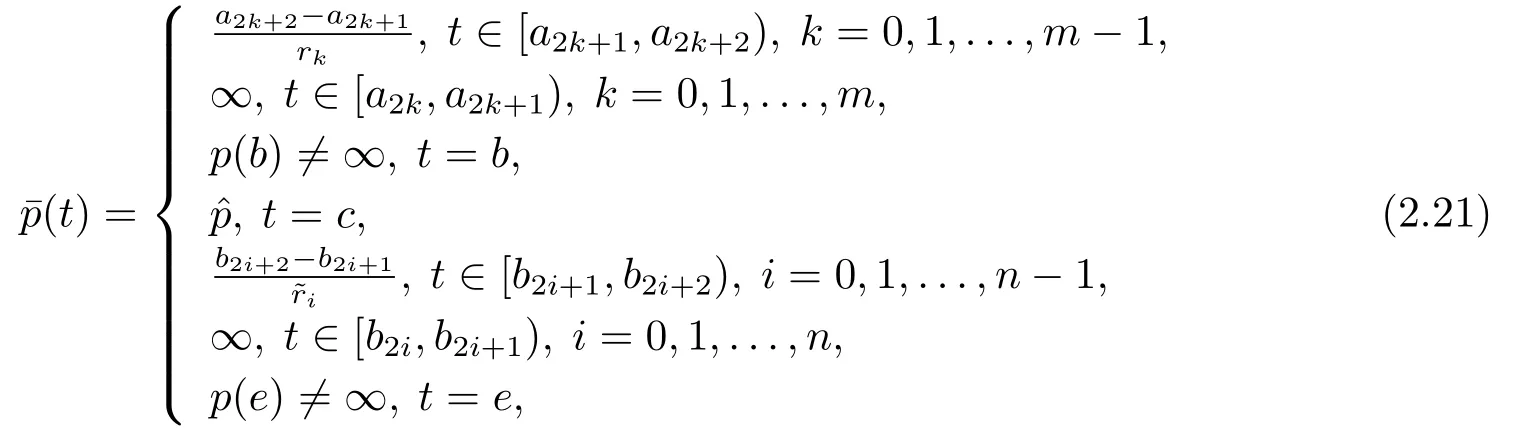


3.證明

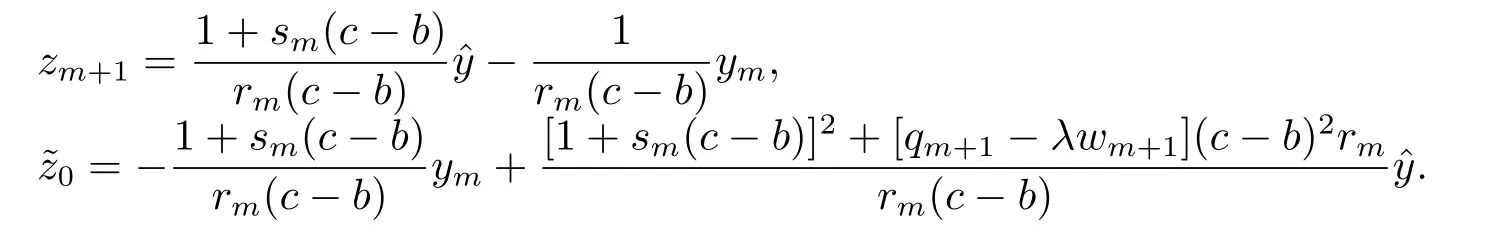


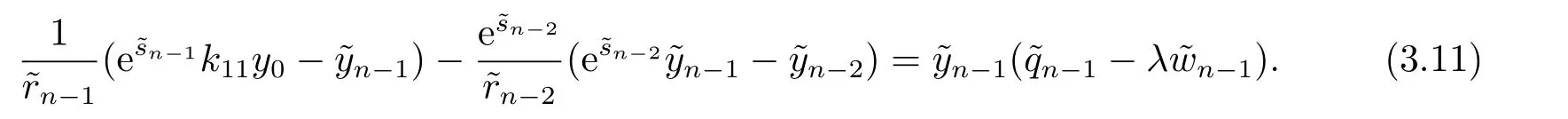



4.矩陣特征值問題的具有分布勢函數(shù)的S-L問題表示


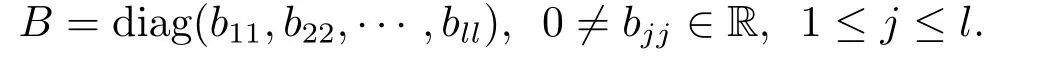

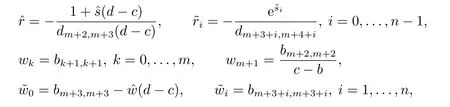
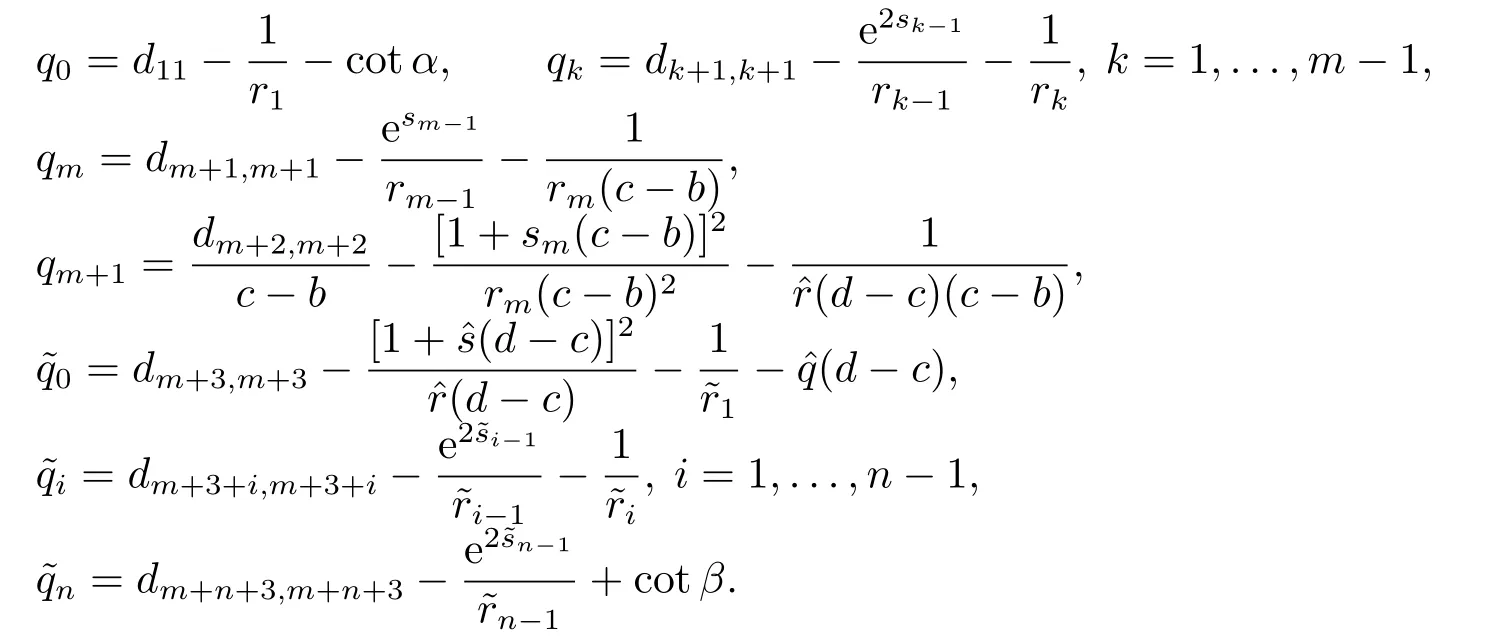


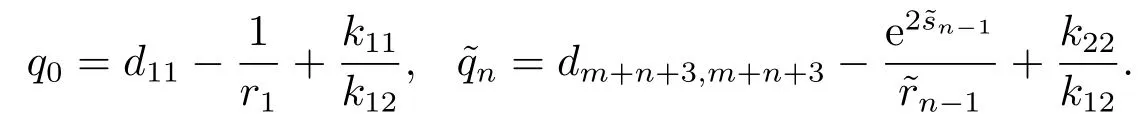
- 應(yīng)用數(shù)學(xué)的其它文章
- Closed-Form Solutions to the Crack and/or Rigid Line Inclusion in 1D Orthorhombic Quasicrystals
- 各向異性橢圓方程雙邊障礙問題解的正則性
- 一類廣義Linard方程周期正解的存在性
- Global Stability of Rarefaction Waves for the One-Dimensional Nonisothermal Compressible Navier-Stokes-Korteweg System
- 廣義嚴(yán)格對角占優(yōu)矩陣的一種判別法
- 次線性期望空間下END列加權(quán)和的完全收斂性

