一個(gè)具有Filippov控制的植物疾病模型的研究
張?zhí)锾?楊友蘋
(山東師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,山東 濟(jì)南 250014)
1 引言
植物疾病作為全球重大關(guān)注問(wèn)題之一,不僅在于植物疾病可以造成不可估計(jì)的經(jīng)濟(jì)損失,嚴(yán)重影響全球經(jīng)濟(jì)發(fā)展,而且在一定程度上決定了人類的生存,對(duì)控制植物疾病至關(guān)重要.到目前為止,已有很多數(shù)學(xué)家運(yùn)用常微方程模型,脈沖微分方程模型等來(lái)研究植物疾病問(wèn)題[1],提出的措施包括噴灑殺蟲(chóng)劑,釋放害蟲(chóng)天敵等,但這些措施實(shí)施的同時(shí)又會(huì)對(duì)環(huán)境造成一定程度的污染,甚至?xí)茐囊欢▍^(qū)域內(nèi)的生態(tài)平衡,因此需要更合理的措施來(lái)控制植物疾病的發(fā)展.目前已有人提出了可以通過(guò)補(bǔ)植無(wú)病植株或者移除染病植株等措施來(lái)達(dá)到控制植物疾病發(fā)展的目的[2-5],并建立了具有經(jīng)濟(jì)閾值和人文控制策略的植物疾病模型,例如文獻(xiàn)[6]提出了一個(gè)具有成比例生長(zhǎng)率的Filippov植物疾病模型,研究了五種類型平衡點(diǎn)的全局穩(wěn)定性;文獻(xiàn)[7]在此基礎(chǔ)上改變了植物的增長(zhǎng)方式,考慮了一個(gè)常數(shù)輸入的生長(zhǎng)率.然而我們發(fā)現(xiàn)考慮一個(gè)具有Logistic增長(zhǎng)的生長(zhǎng)率相對(duì)于植物種群更具有現(xiàn)實(shí)意義.因此,本文以感染植株作為控制目標(biāo),當(dāng)染病植株數(shù)量達(dá)到一定的經(jīng)濟(jì)閾值時(shí),就采取綜合疾病控制策略,即補(bǔ)植無(wú)病植株和移除染病植株,否則不采取任何措施.
2 Filippov植物疾病模型
本文建立如下植物疾病模型:
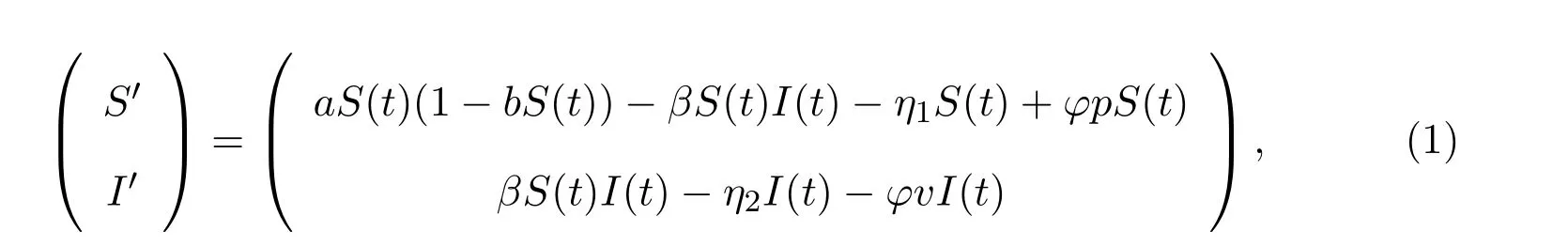
且
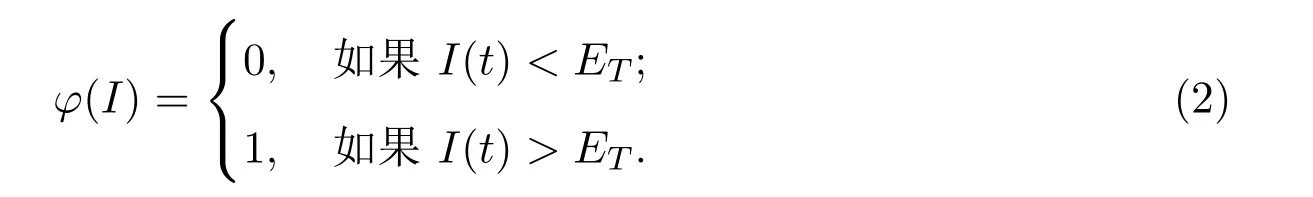
其中S(t)和I(t)分別表示易感植株和感染植株在t時(shí)刻的數(shù)量,a表示易感植株的內(nèi)稟增長(zhǎng)率,表示環(huán)境容納量,β表示感染率,η1和η2分別表示易感植株和感染植株的死亡率,同時(shí)假設(shè)a>η1,p表示易感植株的補(bǔ)植率,v表示感染植株的移除率.令
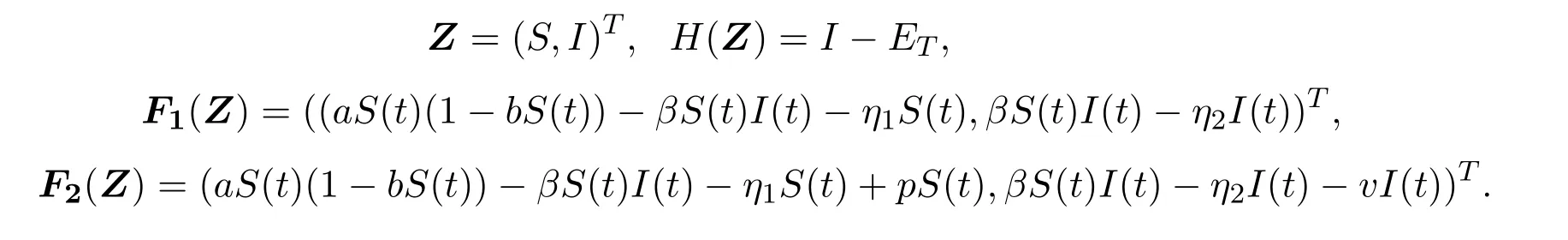
則系統(tǒng)(1)和系統(tǒng)(2)可轉(zhuǎn)化為如下模型,
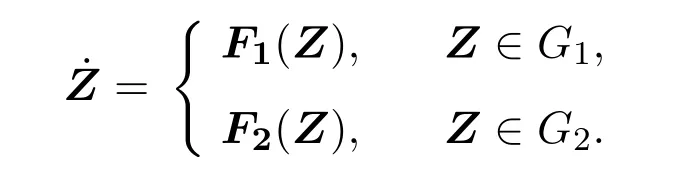
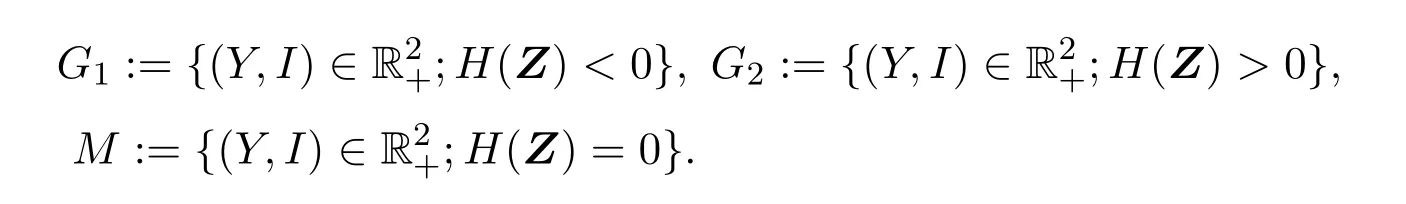
定義2.1 (i)Σ?M是滑動(dòng)段,當(dāng)且僅當(dāng)在Σ上有1(Z)>0且
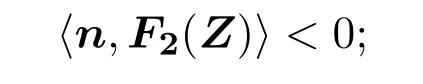
(ii)Σ1?M是逃逸區(qū),當(dāng)且僅當(dāng)在 Σ1上有,其中表示向量積,n=(0,1)T表示H在M上的梯度.
定義2.2 (i)如果F1(D)=0,H(D)<0,或F2(D)=0,H(D)>0,則稱D是真平衡點(diǎn);
(ii)如果F1(D)=0,H(D)>0,或F2(D)=0,H(D)<0,則稱D是假平衡點(diǎn);
(iii)如果λF1(D)+(1?λ)F2(D)=0,H(D)=0,其中 0<λ<1,
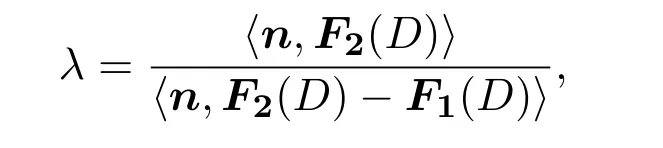
則稱D是偽平衡點(diǎn).
注2.1 由定義可知,只要軌線穿過(guò)不連續(xù)邊界M,系統(tǒng)動(dòng)力學(xué)就會(huì)改變,故一個(gè)假平衡點(diǎn)不可能穩(wěn)定.
3 全系統(tǒng)的動(dòng)力學(xué)性態(tài)
3.1 子系統(tǒng) Gi(i=1,2)的動(dòng)力學(xué)性態(tài)
子系統(tǒng)G1可以寫成如下形式:
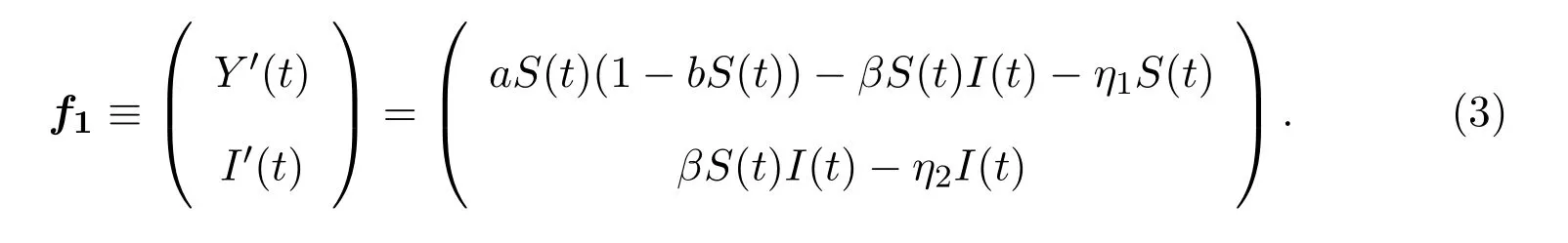
由再生矩陣可得 (3)式的基本再生數(shù)[8-9]為.明顯地,系統(tǒng) (3)存在一個(gè)零平衡點(diǎn)E0=(0,0),無(wú)病平衡點(diǎn)和一個(gè)地方病平衡點(diǎn)
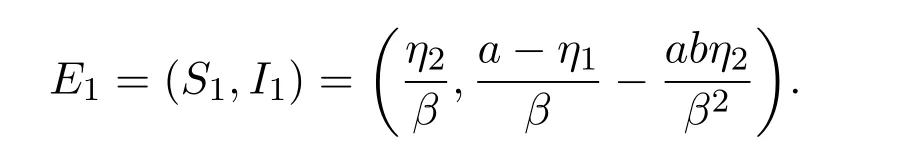
引理3.1 零平衡點(diǎn)E0=(0,0)是鞍點(diǎn);如果R1<1,無(wú)病平衡點(diǎn)局部漸近穩(wěn)定;如果R1>1,地方病平衡點(diǎn)局部漸近穩(wěn)定.
證明系統(tǒng)(3)的雅克比矩陣如下

由a>η1,則 detJ1(E0)=η2(η1?a)<0,故E0是一個(gè)鞍點(diǎn);當(dāng)R1<1時(shí),
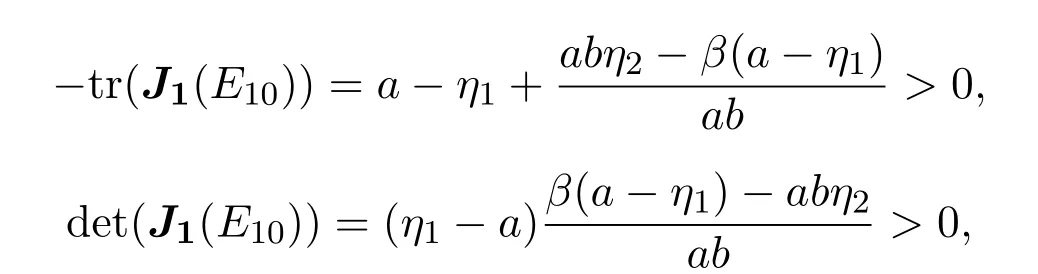
故E10局部漸近穩(wěn)定;當(dāng)R1>1時(shí),?tr(J1(E1))>0,det(J1(E1))>0,故E1局部漸近穩(wěn)定,此時(shí)det(J1(E10))<0,則E10是一個(gè)鞍點(diǎn).
引理3.2系統(tǒng)(3)在無(wú)極限環(huán).
證明令定義Dulac函數(shù)
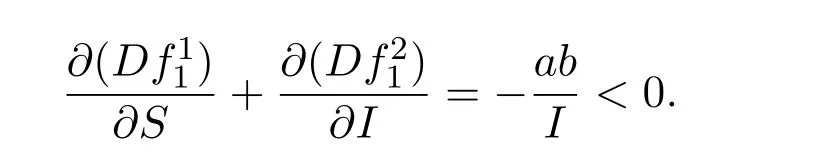
定理3.1 如果R1<1,無(wú)病平衡點(diǎn)E10全局漸近穩(wěn)定;如果R1>1,地方病平衡點(diǎn)E1全局漸近穩(wěn)定.
證明由引理3.1可知,當(dāng)R1<1時(shí),無(wú)病平衡點(diǎn)E10是局部漸近穩(wěn)定的;且由引理3.2可知,系統(tǒng)(3)在無(wú)極限環(huán),故當(dāng)R1<1時(shí),無(wú)病平衡點(diǎn)E10是全局漸近穩(wěn)定的.同理,當(dāng)R1>1時(shí),地方病平衡點(diǎn)E1是全局漸近穩(wěn)定的.
其次,子系統(tǒng)G2可以寫成如下形式:,對(duì)于在單連通區(qū)域內(nèi)的軌線,有
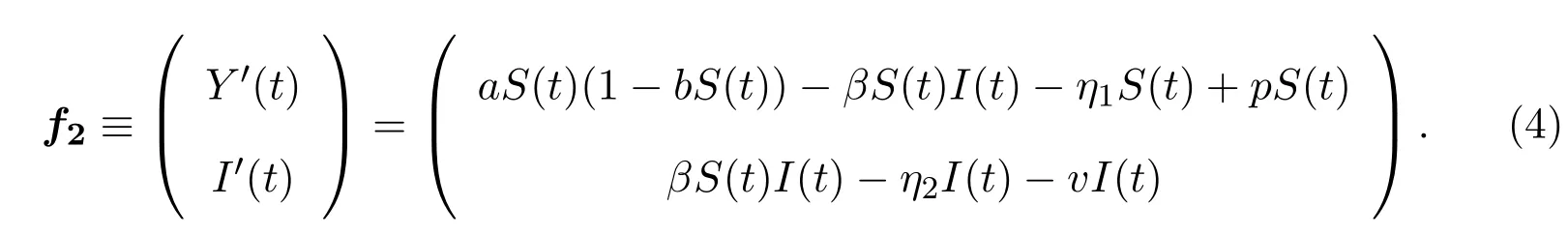
子系統(tǒng)G2的基本再生數(shù)為:
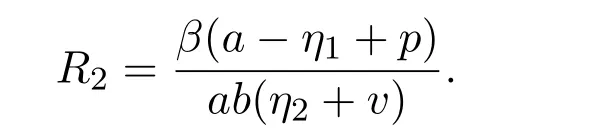
同樣子系統(tǒng)G2存在一個(gè)零平衡點(diǎn)E0=(0,0),無(wú)病平衡點(diǎn)和一個(gè)地方病平衡點(diǎn)
同理于子系統(tǒng)G1的討論,有如下結(jié)論:
定理3.2 如果R2<1,無(wú)病平衡點(diǎn)E20全局漸近穩(wěn)定;如果R2>1,地方病平衡點(diǎn)E2全局漸近穩(wěn)定.
3.2 全系統(tǒng)的動(dòng)力學(xué)性態(tài)
為保證系統(tǒng)(1)正平衡點(diǎn)的存在性,下面只需討論R1>1及R2>1時(shí)全系統(tǒng)的動(dòng)力學(xué)行為.由定義 2.1可知,當(dāng)且時(shí),即
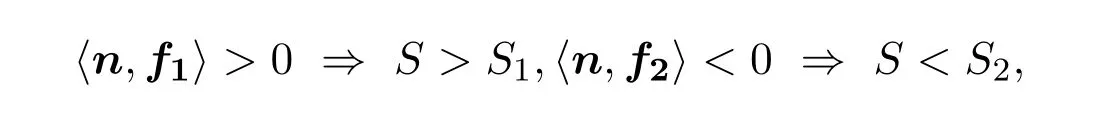
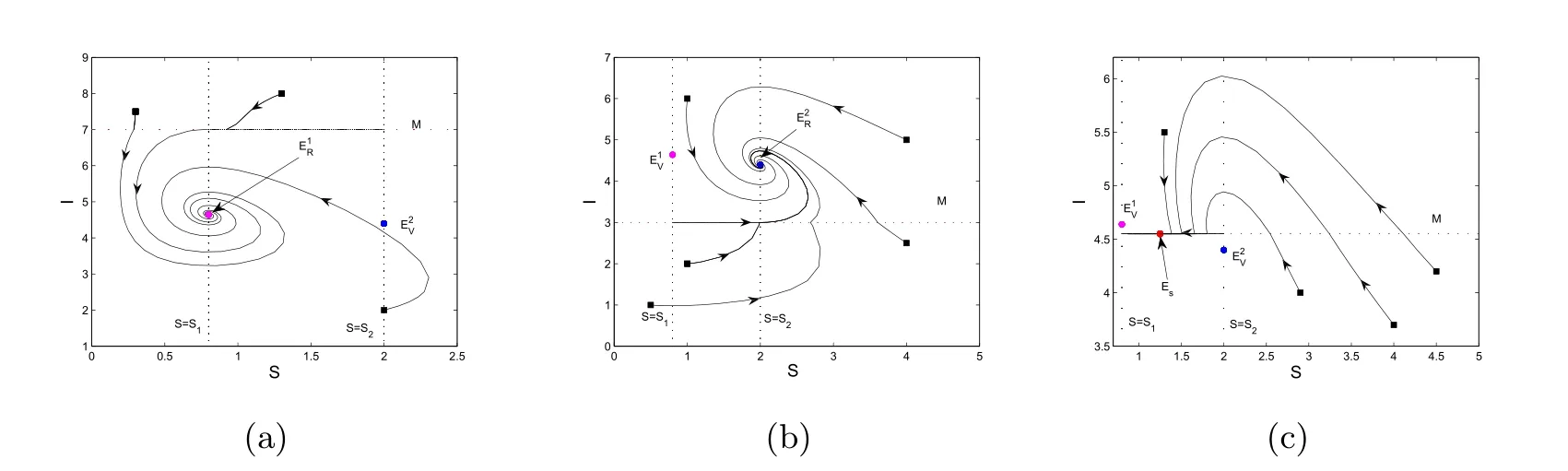
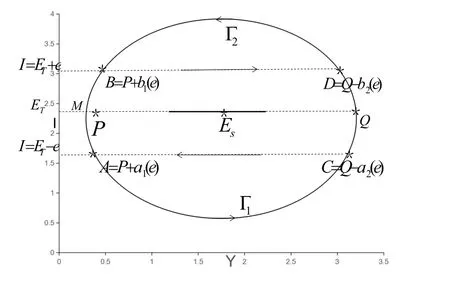
且S1 令g(S(t))=0,得 為保證平衡點(diǎn)的存在性,假設(shè)S?>0,即,則系統(tǒng) (5)存在唯一的滑動(dòng)平衡點(diǎn)Es=(S?,ET),當(dāng)且僅當(dāng)S1 從而g(S(t))關(guān)于S是單調(diào)遞減的,故當(dāng)Es存在時(shí),Es是局部漸近穩(wěn)定的. 依據(jù)閾值ET的取值不同,系統(tǒng)(1)的正平衡點(diǎn)的真假性以及偽平衡點(diǎn)的存在性也不同,通過(guò)數(shù)值模擬(見(jiàn)圖1),做出如下三種情況的猜測(cè): 圖1 (a),(b),(c)分別表示系統(tǒng)(1)真平衡點(diǎn)ER1,真平衡點(diǎn)ER2和偽平衡點(diǎn)Es的全局穩(wěn)定性相圖,切平面 M(I=ET),滑動(dòng)段為 S1S2.η1=0.2,η2=0.4,p=0.6,v=0.6,a=0.3,b=0.2.(a)ET=4.55;(b)ET=7;(c)ET=3. 情況3.1 如果I2 定理3.3 如果I2 證明由引理3.2可知,在子系統(tǒng)G1中無(wú)極限環(huán).同理可證,在子系統(tǒng)G2中無(wú)極限環(huán).下證在滑動(dòng)段附近無(wú)極限環(huán).令假設(shè) Γ是滑動(dòng)段附近的極限環(huán) (見(jiàn)圖 2),線M(I=ET)上下部分分別為 Γ1,Γ2.令Γ和M的交點(diǎn)為P,Q,Γ和線I=ET+e的交點(diǎn)為 Γ和線I=ET?e的交點(diǎn)為A=P+a1(e),C=Q?a2(e),其中e>0足夠小,a1(e),a2(e),b1(e)和b2(e)相對(duì)于e都是連續(xù)的,且 記Γ1和線段AC圍成的區(qū)域?yàn)镈1,Γ2和線段BD圍成的區(qū)域?yàn)镈2,由格林公式,有 圖2 在情況3.1下,對(duì)于系統(tǒng)(1)和系統(tǒng)(2)證明極限環(huán)Γ不存在的示意圖 這與系統(tǒng)(6)是矛盾的,從而在滑動(dòng)段附近無(wú)極限環(huán).因此,如果I2 情況3.2 如果I2 此時(shí),記真平衡點(diǎn)E1為,假平衡點(diǎn)E2為,偽平衡點(diǎn)Es不存在,因此所有起點(diǎn)在G2中的軌線,無(wú)論是否切中滑動(dòng)段,軌線最終都會(huì)進(jìn)入G1,所有G1中的軌線都會(huì)趨于,且是全局漸近穩(wěn)定的,因此無(wú)論軌線的起點(diǎn)是在G1還是G2,它們都將趨于.所以,當(dāng)給定的經(jīng)濟(jì)臨界值取值較大時(shí),系統(tǒng)的解最終穩(wěn)定在子系統(tǒng)G1中,感染植株數(shù)量低于經(jīng)濟(jì)臨界值. 情況3.3 如果ET 記假平衡點(diǎn)E1為,真平衡點(diǎn)E2為,在這種情況下,偽平衡點(diǎn)Es也不存在,則所有起點(diǎn)在G1中的軌線,無(wú)論是否切中滑動(dòng)段,軌線最終都會(huì)進(jìn)入G2,所有G2中的軌線都會(huì)趨于,且是全局漸近穩(wěn)定的,因此無(wú)論軌線的起點(diǎn)是在G1還是G2,它們都將趨于.所以,當(dāng)給定的閾值取值較小時(shí),系統(tǒng)的解最終穩(wěn)定在子系統(tǒng)G2中,感染植株數(shù)量高于經(jīng)濟(jì)臨界值.事實(shí)情況下,選擇一個(gè)相對(duì)較小的經(jīng)濟(jì)臨界值是不合理的,否則將會(huì)造成重大的經(jīng)濟(jì)損失. 本文研究了一個(gè)具有Logistic增長(zhǎng)的植物疾病Filippov模型的動(dòng)力學(xué)性質(zhì),得到了系統(tǒng)的基本再生數(shù)以及平衡點(diǎn)的存在性和穩(wěn)定性,并通過(guò)數(shù)值模擬預(yù)測(cè)了系統(tǒng)的全局穩(wěn)定性.結(jié)果表明,基于閾值的取值,系統(tǒng)的解最終穩(wěn)定在子系統(tǒng)的真平衡點(diǎn)或者滑動(dòng)系統(tǒng)的偽平衡點(diǎn).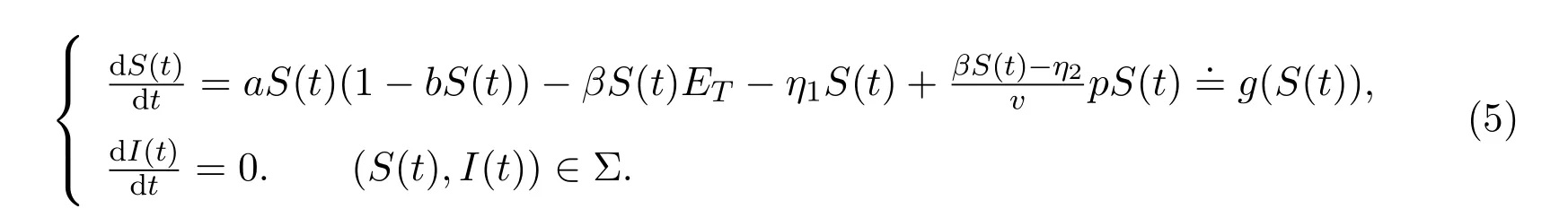
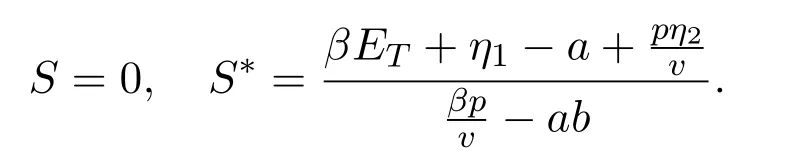
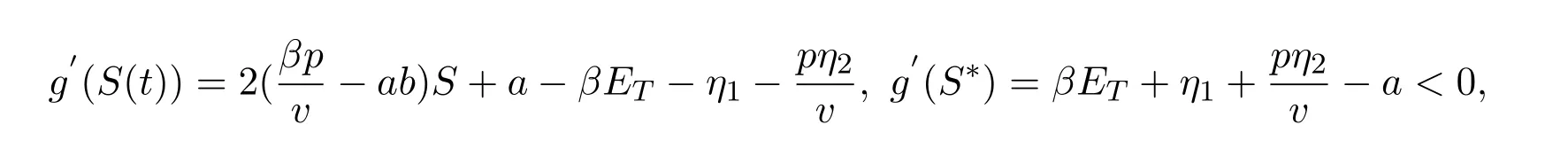
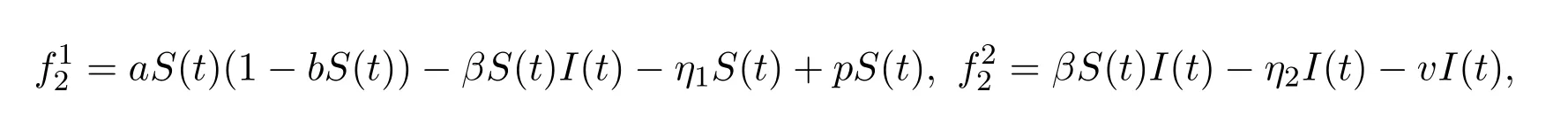
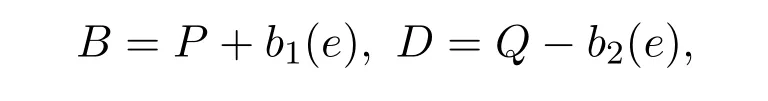
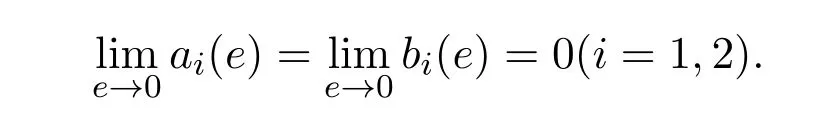
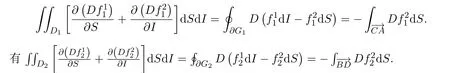

4 結(jié)論

