Xianyong YANG(楊先勇)

School of Preparatory Education,Yunnan Minzu University,Kunming 650500,China School of Mathematics and Statistics,Central south University,Changsha 410205,China E-mail:ynyangxianyong@163.com

Wei ZHANG(張薇)

Department of Mathematics,Yunnan University,Kunming 650500,China E-mail:weizyn@163.com

Fukun ZHAO(趙富坤)?

Department of Mathematics,Yunnan Normal University,Kunming 650500,China E-mail:fukunzhao@163.com

Abstract In this article,we are concerned with the existence of solutions of a quasilinear elliptic equation in RNwhich includes the so-called modi fied nonlinear Schr?dinger equation as a special case.Combining the dual approach and the nonsmooth critical point theory,we obtain the existence of a nontrivial solution.

Key words nontrivial solution;quasilinear elliptic equation;nonsmooth critical point theory;dual approach

1 Introduction

In this article,we consider the existence of a nontrivial solution of the following quasilinear elliptic equation of Schr?dinger type

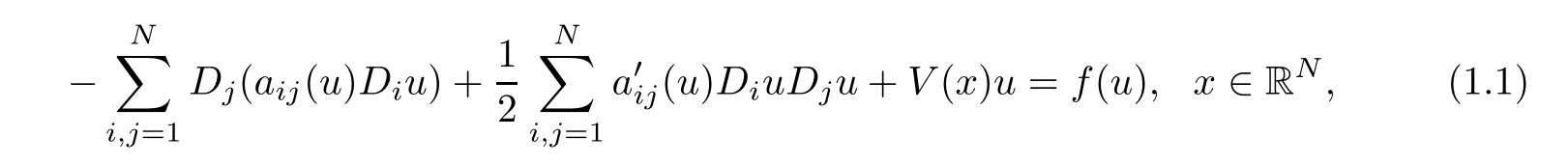
The quasilinear Schr?inger equation(1.3)was derived as models of several physical phenomena,see for example[1,14].

Observe that,formally(1.2)is the Euler-Lagrange equation associated to the following functional

On the other hand,it is worth mentioning that the authors in[23]concerned the following generalized quasilinear Schr?inger equations

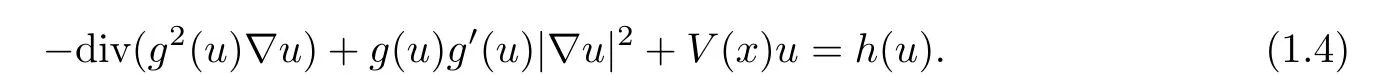
By introducing a new variable replacement(see[7]and[4]),they build the existence of nontrivial solutions of it.Noting that equation(1.4)will reduce to equation(1.2)provided that g2(u)=1+2u2,they extended the results in[5]in some sense since both the problem and the method are more general.The critical exponent was found recently in[7],[9]and[12]and the existence of positive solutions was established.

Recently there has been an increasing focus on the existence of solutions to the quasilinear elliptic equations similar to(1.1).In[19],Liu,Wang and Guo constructed multibump type solutions of an quasilinear elliptic equation with a periodic potential,where the nonsmooth critical point thoery was involved.The existence of in finitely many geometrically distinct solutions was obtained in[20]and[30].In[15],the authors obtained the existence and multiplicity of sign-changing solutions via the invariant set of descend flows theory and the perturbation method.Wu and Wu[29]established the existence results of positive solutions,negative solutions and a sequence of high energy solutions to(1.1)via the perturbation method.We refer to[6]and[31]for the case that the Hardy term was involved.

It is a natural question that whether one can study problem(1.1)via the method of changing of variables?It seems that the first answer to the above question is due to Wu and Wu[28].They introduced the following change of variables

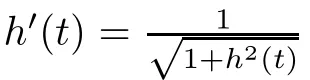
In order to state the main result,we give some assumptions:

(g1)g∈C1(R,R)is a even function and nondecreasing about|t|.Morevoer,for t∈R,g(t)≥g(0)>0.

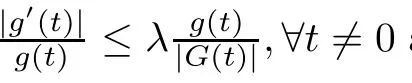
(f1)f∈C(R,R).

(f2)(f3)There exist C>0 andsuch that

(f4)There existsμ>2 such that 0<μg(t)F(t)≤G(t)f(t)for all t∈R{0},whereR

(a1)aij∈C1(R,R)and there exists c>0 such that

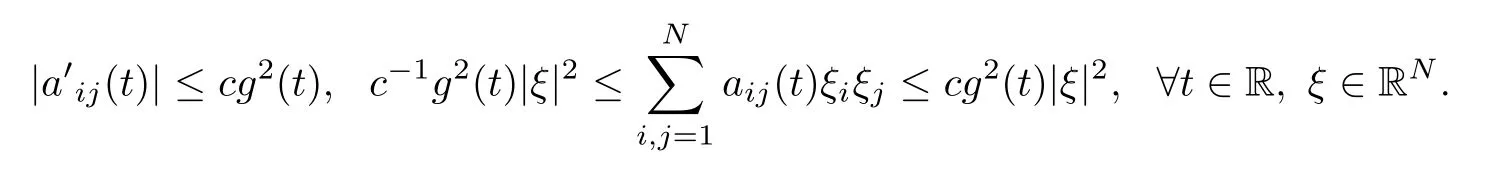
(a2)There exists 0<α<μ?2 such that

for all t∈ R and ξ∈ RN.

In order to avoid some confusion,we appoint that g and G appeared in the rest of our paper denote the functions satisfying our above assumptions without any explanation.

Remark 1.1Let aij(t)=(1+2t2)δij(s),g2(t)=1+2t2and f:RN7→ R be H?lder functional satisfying the above assumptions

(f2)′There exist C>0 and 2≤ p<22?=such that|f(t)|≤ C(1+|t|p?1).

(f3)′There existsμ>4 such that 0< μF(t)≤ tf(t),for all t∈ R{0},where F(t)=

The above hypotheses of nonlinearity f appeared in some works in which the existence and multiplicity results have been obtained(see[5]and[21]).By the de finitions of aijand g as well as the hypotheses of(f1)′–(f3)′,we claim that(g1)–(g2),(a1)–(a2)and(f1)–(f4)also hold.In fact,by a direct calculation,we obtain thatfor allAs the statement of[23],(f1)′–(f3)′imply(f1)–(f4),it is worth noting that(f3)and(f4)seem to be originally used in it.The rest of the conclusions are trivial.

The weak form of(1.1)is

Obviously,E is not well de fined in H1(RN).To overcome this difficulty,inspired by[23],we make a change of variable constructed as

Letting

then

By the following Lemma 2.1 and Sobolev imbedding theorem,it is easy to see that I is well de fined in H1(RN).

Here are the main results of this paper.

Theorem 1.3Under the assumptions of(V),(g1)–(g2),(a1)–(a2)and(f1)–(f4),problem(1.1)has at least a nontrivial solution.Moreover,if,then u∈L∞(RN).

Example 1.40<λ<1 is required in assumption(g2),we gave a example for the case(see Remark 1.1).Takingby a direct calculation,we can see that(g2)is satis fied for,which implies that it also may occur for the case

The article is organized as follows.In Section 2,we will first prove some preliminary lemmas.In Section 3,we give the mountain pass structure of nonsmooth version.In Section 4,we focus on the proof of Theorem 1.3.

Throughout this article,→anddenote the strong convergence and the weak convergence,respectively.H=H1(RN)is the normal Sobolev space with the inner productand the normdenotes the norm in Ls(RN)for 1≤s≤∞.c,C0,C,Cidenote the di ff erent positive constants whose value may change from line to line but are not essential to the analysis of the proof.

2 Preliminaries

Lemma 2.1Under the assumptions(g1)–(g2),(a1)–(a2)and(f1)–(f4),the functions f(t),F(t),g(t),G(t),bij(t)andenjoy the following properties.

(1)G(t)and G?1(t)are odd nondecreasing functions.

(3)For every ?>0,there exists C?>0 such that

for all t∈R.

(4)There exists C>0 such that|bij(t)|≤ C andfor all t∈R.

(5)There exist c1>0 and c2>0 such that

for all t∈ R and ξ∈ RN.

ProofItem(1),(2),(4),(5)can be easily deduced from our assumptions and the de finitions of bij.As for item(6),it can be found in[23]and[24],so we only give the proof of item(3).

By(f2),for every ?>0,there exists δ= δ(?)>0 such that|f(t)| ≤ ?|t|for all 0<|t|< δ.Using(f3),for g(t)|G(t)|p?1≥ 1,we have|f(t)|≤ Cg(t)|G(t)|p?1.Noting thatthere exists M>0 such that A ? [0,M],where A={t∈R|g(t)|G(t)|p?1≤ 1}.This together with the continuity of f,there exists C0>0 such that|f(t)|≤ C0for all t∈ A.So|f(t)|≤ ?|t|for all t∈ {t∈ A|0<|t|< δ}.For t∈ {t∈ A||t|≥ δ},noting that g(t)|G(t)|p?1is an increasing function,we have

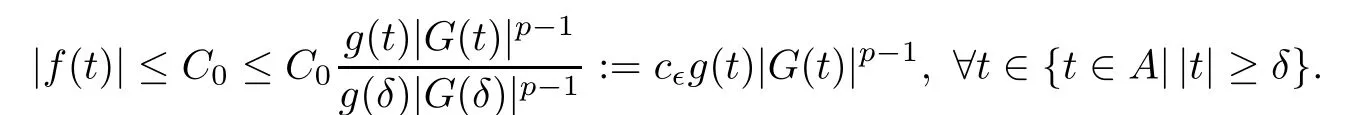
Therefore

Lemma 2.2Assume that(g1)–(g2),(a1)–(a2)and(f1)–(f4)hold,then the functional I∈C(H,R)and the derivatives of I exist along the direction H∩L∞(RN),that is

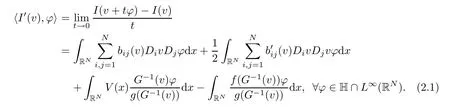
ProofObviously,by Lemma 2.1,(V)and Sobolev imbedding theorem,I is well de fined on H.Assume that{vn}?H be a sequence such that vn→v in H,up to a subsequence,we have vn→ v in Ls(RN)for 2≤ s≤ 2?,in L2(RN),vn(x)→ v(x)a.e.x∈RN,anda.e.x∈RN.By Lemma A.1 in[26],there exist hp∈Lp(RN)and h2∈ L2(RN)such that|vn(x)|≤ hp(x)and|?vn(x)|≤ h2(x)a.e.x∈ RN.Now,by applying Lemma 2.1,(V)and the Lebesgue dominated theorem,we have

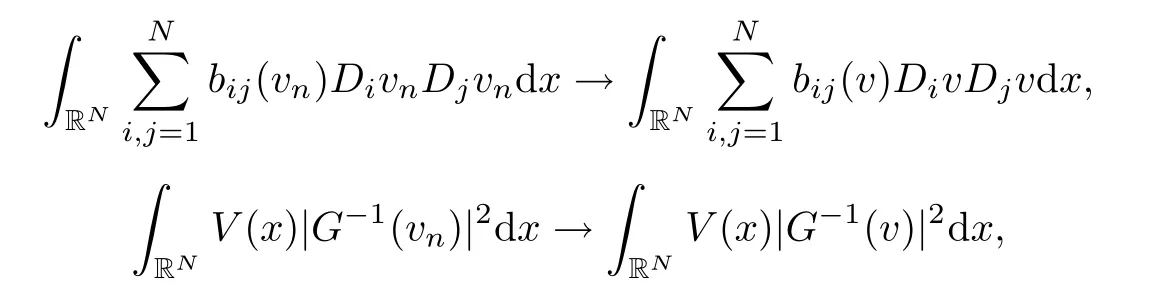
and

These imply that I(vn)→I(v)and I is continuous in H.Letting

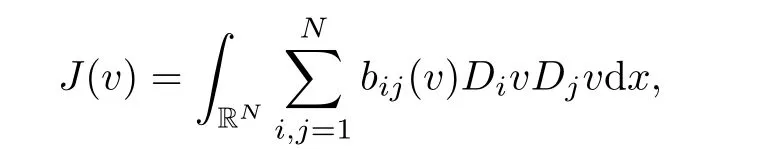
by Lemma 2.1 and the H?lder inequality,we deduce that

It follows from the Lebesgue dominated convergence theorem that

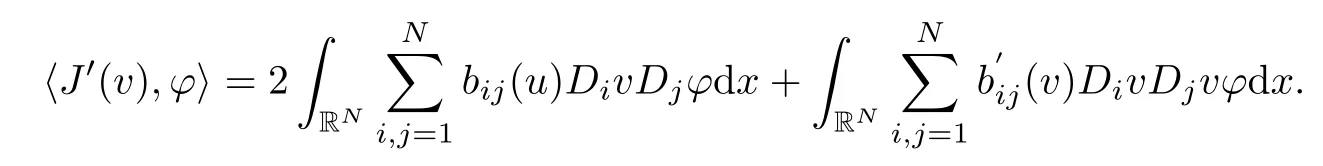
Similarly,we can prove(2.1).As the proof of I∈C(H,R),it can be proved that the functional χ(v):=hI′(v),?i is continuous for each ? ∈ H ∩ L∞(RN). ?

Lemma 2.3If v ∈ H ∩ C2(RN)satis fies hI′(v),?i=0 for all ? ∈ H ∩ L∞(RN),then u=G?1(v)is a solution of(1.1).

ProofhI′(v),?i=0 for all ? ∈ H ∩ L∞(RN)is equivalent to

A standard argument shows that v∈H is a solution of the following equation

where ν denotes the outward normal to ?BR.Consequently,

which implies(2.2).By the de finition of bij,we have

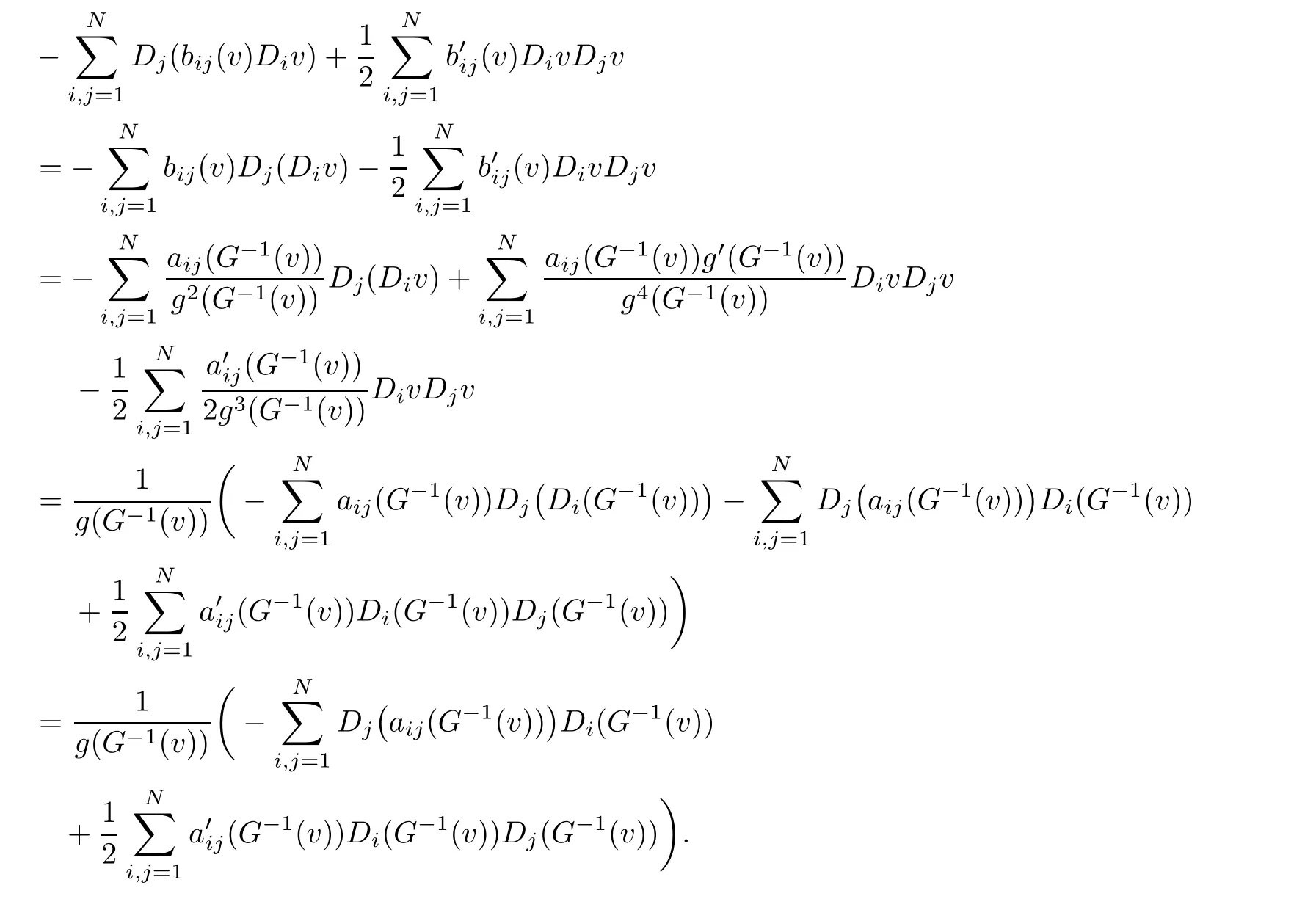
This together with(2.2),we obtain

which implies that u=G?1(v)is a solution of(1.1).The proof is completed.

ProofFor any v∈H,by Lemma 2.1,(a2)and(g2),we deduce that

3 Mountain Pass Framework

Lemma 3.1I satis fies the mountain pass geometry,that is,

(1)There exist ρ,c>0 such that I(v)≥ c for all kvk= ρ.

(2)There exists v∈H satisfying kvk>ρ such that I(v)<0.

Proof(1) If g is bounded,it is clear thatfor all t ∈ R,whereThis together with the(2),(3),(5)of Lemma 2.1 and the Sobolev imbedding theorem,we have

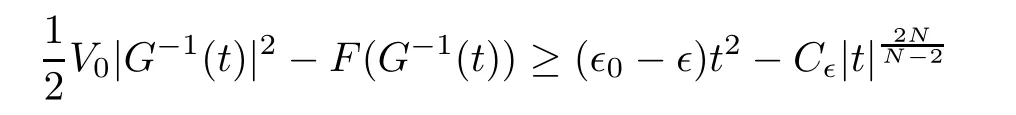
for all t∈R,where(2),(3)of Lemma 2.1 are used.Therefore

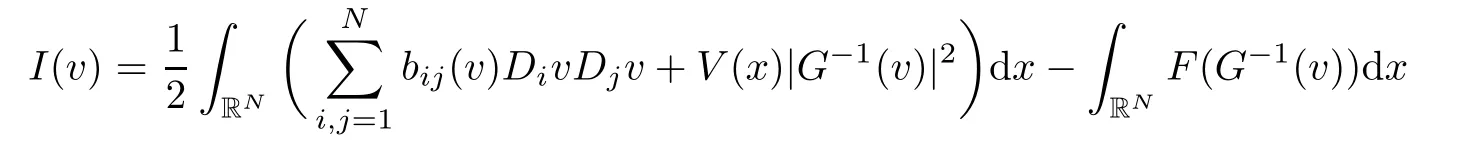
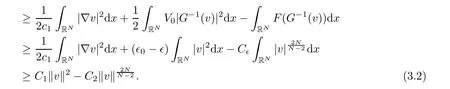
The conclusion follows from(3.1)and(3.2)if we choose ρ small enough.

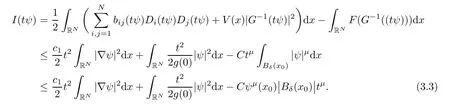
Thus,we can choose v=Tψ with T>0 large enough such that I(v)<0 and the proof is completed. ?

In order to obtain the solution of(1.1),we first introduce the following notation of the weak slope.

De finition 3.2(see[2]and[13]) Let I:X→R be a continuous function and let u∈X.We denote by|dI|(u)the supremum of the σ′in[0,∞)such that there exist δ>0 and a continuous map H:B(u,δ)× [0,δ]→ X satisfying d(H(v,t))≤ t and d(H(v,t),v)≤ t for all(v,t)∈ B(u,δ)× [0,δ].The extended real number|dI|(u)is called the weak slope of I at u.

Lemma 3.3(see[28]) |dI|(u)≥ sup{|hI′(v),?i|:? ∈ H∩L∞(RN),k?k=1}.

By the nonsmooth Mountain Pass theorem without(PS)-condition(see for example[10],[11]),there exists{vn}?H be a sequence satisfying I(vn)→c and|dI|(vn)→0,whereΓ ={γ ∈ C([0,1],H):γ(0)=0,I(γ(1))<0}.

Lemma 3.4The sequence{vn}is bounded in H.

ProofLet{vn}be a sequence with I(vn)→c and|dI|(vn)→0.It follows from Lemma 3.3 that

Hence,

Let T>0,vT=v for|v|≤ T and vT=sign(v)T for|v|≥ T.Settingthen(see Theorem 5.4.4 in[22]).Consequently,

Letting T→∞and using Lemma 2.4,we have

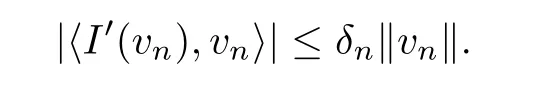
This together with(g1),(a2),and(f4),for n large enough,we have

(3.4)–(3.6)imply that{vn}is bounded in H.

Lemma 3.5There exist τ,R>0,and{yn} ? RNsuch that

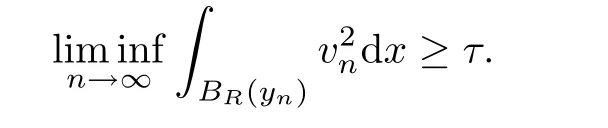
ProofAssume by contradiction,for all R>0,there holds

By using Lemma 1.21 in[26]and its proof,we have vn→ 0 in Ls(RN)for s∈ [2,2?).By Lemma 2.1,we have

and

(3.8)leads to

Passing to a subsequence,we can assume that

and

Moreover,by Lemma 2.1 again,we obtain

Combining(3.7)and(3.10)–(3.11),we have I(vn)→ 0,which contradicts that I(vn)→ c>0.?

4 Proof of Theorem 1.3

ProofIn view of the boundedness of{vn}in H,up to a subsequence,we can assume thatin H,vn→v infor s∈ [2,2?),and vn(x)→ v(x)a.e x∈ RN.Using these facts and|dI|(vn)→0,a standard argument shows that

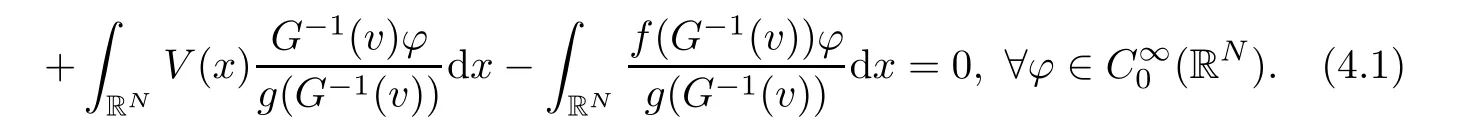
Claim 1v is nontrivial.

Case 1V(x)=V∞.Because I and I′are invariant up to a translation,we can easily deduce thatby using Lemma 3.5.

Case 2.Assume by contradiction,passing to a subsequence,we can assume that

Let the function I∞:H→R de fined by

It is easy to see that

and

Let wn(x)=vn(x+yn),where{yn}is the sequence obtained in Lemma 3.5,then

As the proof of Lemma 3.4,there exists w∈H{0},passing to a subsequence,we can assume that

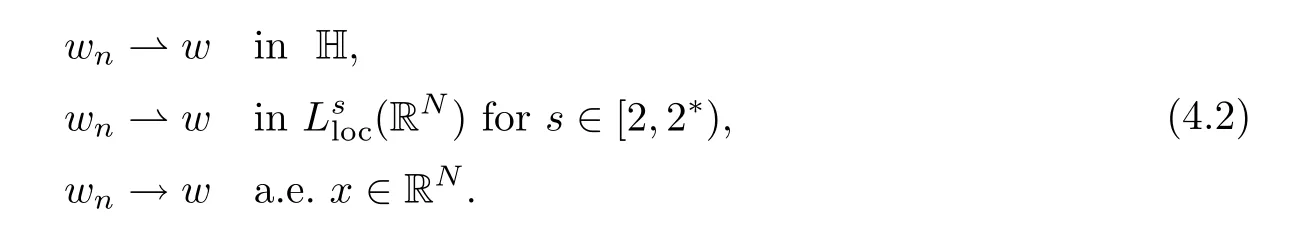
It is easy to see that w is a solution of the following equation

Using the regularity theory in[18],we have the following Pohozaev identity

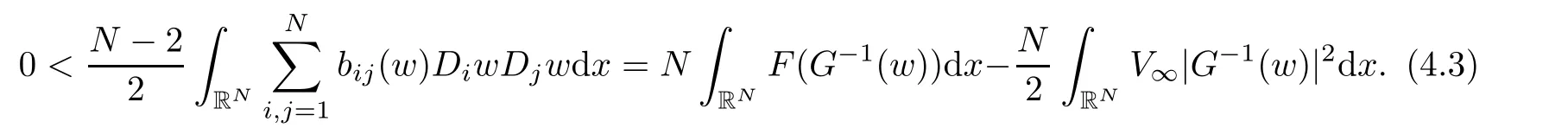
Thus

This implies that

De fine

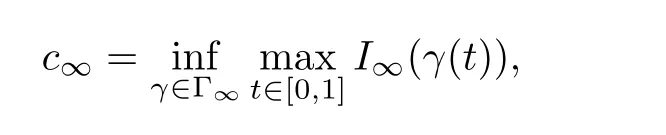
Letting

By the H?lder inequality,the Lebesgue dominated convergence theorem and(4.2),we have

(4.5)–(4.7)imply that

In the following,we might as well suppose{yn}obtained in Lemma 3.5 satisfying|yn|→ ∞,as n→∞.Otherwise,{|yn|}is bounded.Then,by using the fact that vn→v inwe haveand the conclusion holds.|yn|→∞deduce that

Hence c≥c∞,which leads to a contradiction.Consequently,

Claim 2If,then v∈L∞(RN).Obviously,v satis fies the following equation

Let T>0,vT=v for|v|≤ T and vT=sign(v)T for|v|≥ T.

We claim that

Similarly,as T→∞,we have

Together with(4.10)–(4.13),for r>0,we have

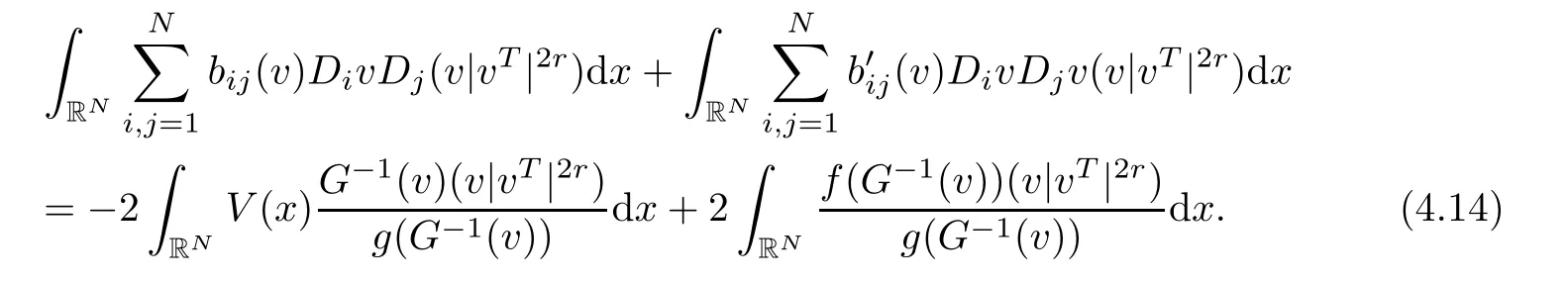
Combining Lemma 2.1 and Lemma 2.4,we have

Lemma 2.1 and the H?lder inequality imply that

Letting T→∞,then

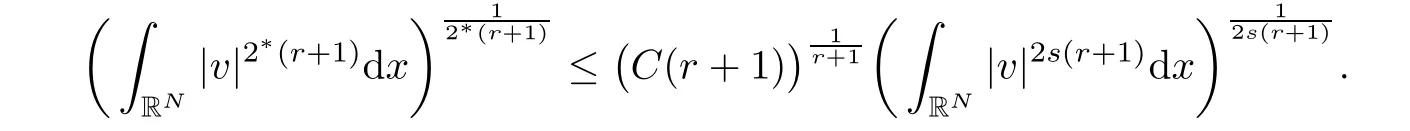
Taking r0=0 and 2s(rk+1+1)=2?(rk+1),we obtain

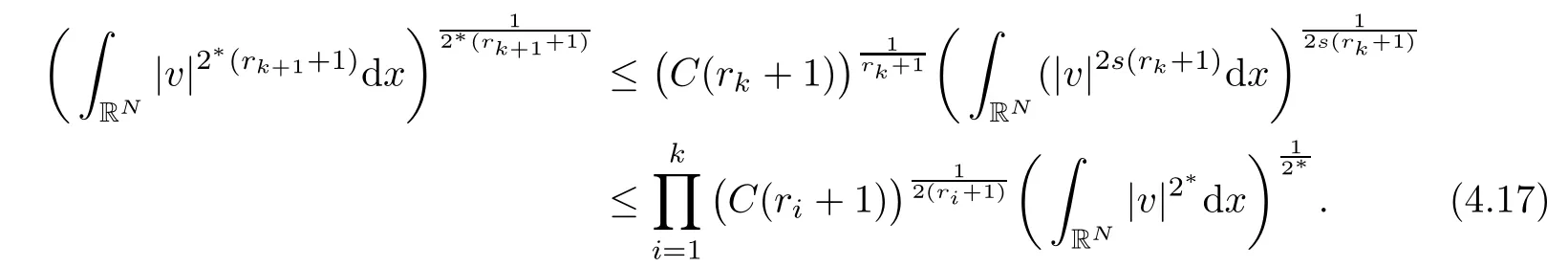
Letting k→∞,there holds

By the regularity theory,we have v∈C2(RN).This together with Lemma 2.3 deduce that u=G?1(v)is a solution to problem(1.1).By applying Claim 2 and the continuity of G?1(t),u∈L∞(RN)as?

AcknowledgementsThe authors would like to thank Dr.Ke Wu for helpful suggestions on the present article,as well as bringing their attention to[28]and[23].