Iz-iddine EL-FASSI

Department of Mathematics,Faculty of Sciences,Ibn Tofa?l University,B.P.133,Kenitra,Morocco E-mail:izidd-math@hotmail.fr;izelfassi.math@gmail.com

Hamid KHODAEI

Department of Mathematics,Malayer University,P.O.Box 65719-95863,Malayer,Iran E-mail:hkhodaei.math@gmail.com

Themistocles M.RASSIAS

Department of Mathematics,National Technical University of Athens,Zografou Campus,15780,Athens,Greece E-mail:trassias@math.ntua.gr

Abstract In this paper,using the Brzd?k’s fixed point theorem[9,Theorem 1]in non-Archimedean(2,β)-Banach spaces,we prove some stability and hyperstability results for an p-th root functional equation

Key words fixed point theorem;p-th root functional equation;stability;non-Archimedean(2,β)-normed spaces

1 Introduction and Preliminaries

Throughout this paper,N and R denote the sets of all positive integers and real numbers,respectively;we put N0:=N∪{0},R0:=R{0},and R+=[0,∞),and let F denote the field of real or rational numbers,and we write BAto mean the family of all functions mapping from a nonempty set A into a nonempty set B.In the rest of this paper,unless otherwise explicitly stated,we assume that k ∈ N{1},p ∈ {1,···,5},a1,···,akare fixed nonzero reals when p∈{1,3,5}and are fixed positive reals when p∈{2,4}.

The theory of 2-normed spaces was first developed by G?hler[21]in the mid 1960s,while that of 2-Banach spaces was studied later by G?hler[22]and White[38].In 1897,Hensel[26]introduced a normed space which does not have the Archimedean property.It turns out that non-Archimedean spaces have many nice applications(see[28,30,33]).

De finition 1.1By a non-Archimedean field,we mean a field K equipped with a function(valuation)|·|?:K → [0,∞)such that for all r,s ∈ K,the following conditions hold

(1)|r|?=0 if and only if r=0;

(2)|rs|?=|r|?|s|?;

(3)|r+s|?? max(|r|?,|s|?)for all r,s ∈ K.

Clearly,|1|?=|? 1|?=1 and|n|?? 1 for all n ∈ N.The function|·|?is called the trivial valuation if|r|?=1,?r ∈ K,,and|0|?=0.

De finition 1.2Let E be a vector space over a scalar field K with a non-Archimedean non-trivial valuation|·|?.A function k ·k?:E → R+is non-Archimedean norm(valuation)if it satis fies the following conditions

(1)kxk?=0 if and only if x=0;

(2)krxk?=|r|?kxk?for all r∈ K and x ∈ E;

(3)kx+yk?? max(kxk?,kyk?)for all x,y ∈ E.

Then(E,k ·k?)is called a non-Archimedean space or an ultrametric normed space.

Due to the fact that

in which n>m,the sequence{xn}is Cauchy if and only if{xn+1?xn}converges to zero in a non-Archimedean normed space.In a complete non-Archimedean space,every Cauchy sequence is convergent.

Example 1.3Fix a prime number p.For any nonzero rational number x,there exists a unique positive integer nxsuch that,where a and b are positive integers not divisible by p.Then|x|p:=p?nxde fines a non-Archimedean norm on Q(the set of rational numbers).The completion of Q with respect to the metric d(x,y)=|x?y|pis denoted by Qp,which is called the p-adic number field.In fact,Qpis the set of all formal series,where|ak|?p?1.The addition and multiplication between any two elements of Qpare de fined naturally.The normis a non-Archimedean norm on Qpand Qpis a locally compact field.

Now,we give some basic concepts concerning the non-Archimedean(2,β)-normed space.

De finition 1.4Let X be a real vector space with dimX?2 over a scalar field K with a non-Archimedean non-trivial valuation|·|?and β be a fixed real number with 0< β ? 1.A function k·,·k?,β:X × X → R+is called a non-Archimedean(2,β)-norm on X if and only if it satis fies

(N1)kx,yk?,β=0 if and only if x and y are linearly dependent;

(N2)kx,yk?,β=ky,xk?,β;

(N4)kx+y,zk?,β? max{kx,zk?,β,ky,zk?,β}

for all x,y,z ∈ X and λ ∈ K.The pair(E,k·,·k?,β)is called a non-Archimedean(2,β)-normed space.

If x ∈ X and kx,yk?,β=0 for all y ∈ X,then x=0.Moreover;the functions x → kx,yk?,βare continuous functions of X into R+for each fixed y∈X.

The basic de finitions of a non-Archimedean(2,β)-Banach space are given as follows

(a)A sequence{xn}in a non-Archimedean(2,β)-normed space X is called a convergent sequence if there is an x∈X such thatfor all y ∈ X.In this case,we write

(b)A sequence{xn}in a non-Archimedean(2,β)-normed space X is called a Cauchy sequence if and only if{xn+1?xn}converges to zero in X.

(c)A non-Archimedean(2,β)-normed space in which every Cauchy sequence is a convergent sequence is called a non-Archimedean(2,β)-Banach space.

We remark that the concept of a non-Archimedean(2,β)-normed space is a generalization of a non-Archimedean 2-normed space(β=1).

Example 1.5Let K be a non-Archimedean field equipped with a non-trivial valuation|·|?.For λ ∈ K and x=(x1,x2),y=(y1,y2) ∈ X=K2with x+y=(x1+y1,x2+y2)and λx=(λx1,λx2),the non-Archimedean(2,β)-norm on X could be de fined by

where β is a fixed real number with 0< β ? 1.

The concept of stability of a functional equation arises when one replaces a functional equation by an inequality which acts as a perturbation of the equation.In 1940,Ulam[37]posed the first stability problem.In the next year,Hyers[27]gave the first affirmative answer to the question of Ulam for Banach spaces.Hyers theorem was generalized by Aoki[4]for additive mappings and by Rassias[34]for linear mappings by considering an unbounded Cauchy di ff erence.The concept of the Hyers-Ulam-Rassias stability originated from Rassias paper[34]for the stability of functional equations(see also[1,6,11,12,20,23,24,32,35,36,39]).

The first hyperstability result appears to be due to Bourgin[5].However,the term hyperstability was used for the first time in[31].Numerous papers on this subject have been published and we refer to[7,10,13,14,16,19].Recently,the stability problem and hyperstabilty results for the functional equations of the radical type in 2-Banach spaces and in some other generalized spaces has been also studied,for example see[2,3,14–18,29].In 2017,Brzd?k[8]gave some remarks on solutions to the functional equations of the radical type.

Let X be a vector space over F.We say that a function f:R→X satis fies the p-th root functional equation if

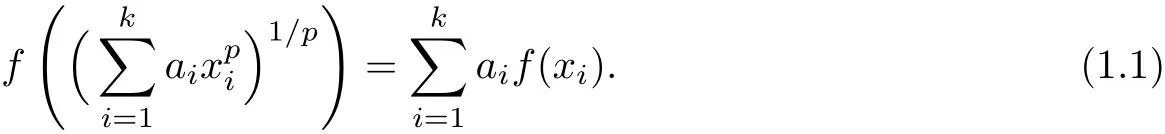
In 2014,Gordji et al.[25]studied the general solution and some stability results for the functional equation(1.1)in β-Banach spaces.

Theorem 1.6(see[25,Theorem 3]) Let X be a vector space over F.If a mapping f:R→X satis fies the functional equation(1.1)and,then for each p=1,···,5,f is Cauchy-additive,quadratic,cubic,quartic and quintic,respectively.

The aim of this paper is to study the generalized stability and hyperstability for the the p-th root functional equation(1.1)by using the fixed point theorem[9,Theorem 1]in non-Archimedean(2,β)-Banach space.At the end of this article we will give some important consequences from our main results.Our results are improvements and generalizations of many works referenced in[2,3,14–16,29].

2 Fixed Point Theorem

In this section,we rewrite the fixed point theorem[9,Theorem 1]in non-Archimedean(2,β)-Banach space.For it we need to introduce the following hypotheses.

(H1)W is a nonempty set and X is a non-Archimedean(2,β)-Banach space.

(H2)f1,···,fj:W → W and K1,···,Kj:W × X → R+are given maps.

(H4)T:XW→XWis an operator satisfying the inequality

for all ξ,μ ∈ XW,x ∈ W and y ∈ X.

The basic tool in this paper is the following fixed point theorem.

Theorem 2.1Assume that hypotheses(H1)–(H4)are satis fied.Suppose that there are functions ε:W ×X → R+and ? :W → X such that

and

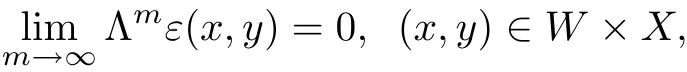
then for every x∈W the limit

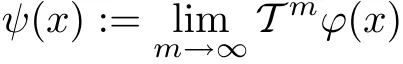
exists and the function ψ∈XW,de fined in this way,is a fixed point of T with

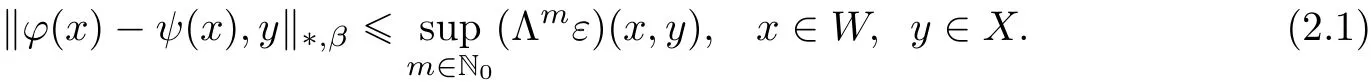
Moreover,if

then ψ is the unique fixed point of T satisfying(2.1).

3 Stability Result for Eq.(1.1)

The following theorem is the main result of this paper.It was motivated by the issue of Ulam stability,which concerns approximate solutions of a functional equation(1.1)in non-Archimedean(2,β)-Banach spaces by applying the fixed point Theorem 2.1.

Theorem 3.1Let X be a non-Archimedean(2,β)-Banach space.Let f:R → X,c:R0→R+and L:×X→R+be functions satisfying the following three conditions

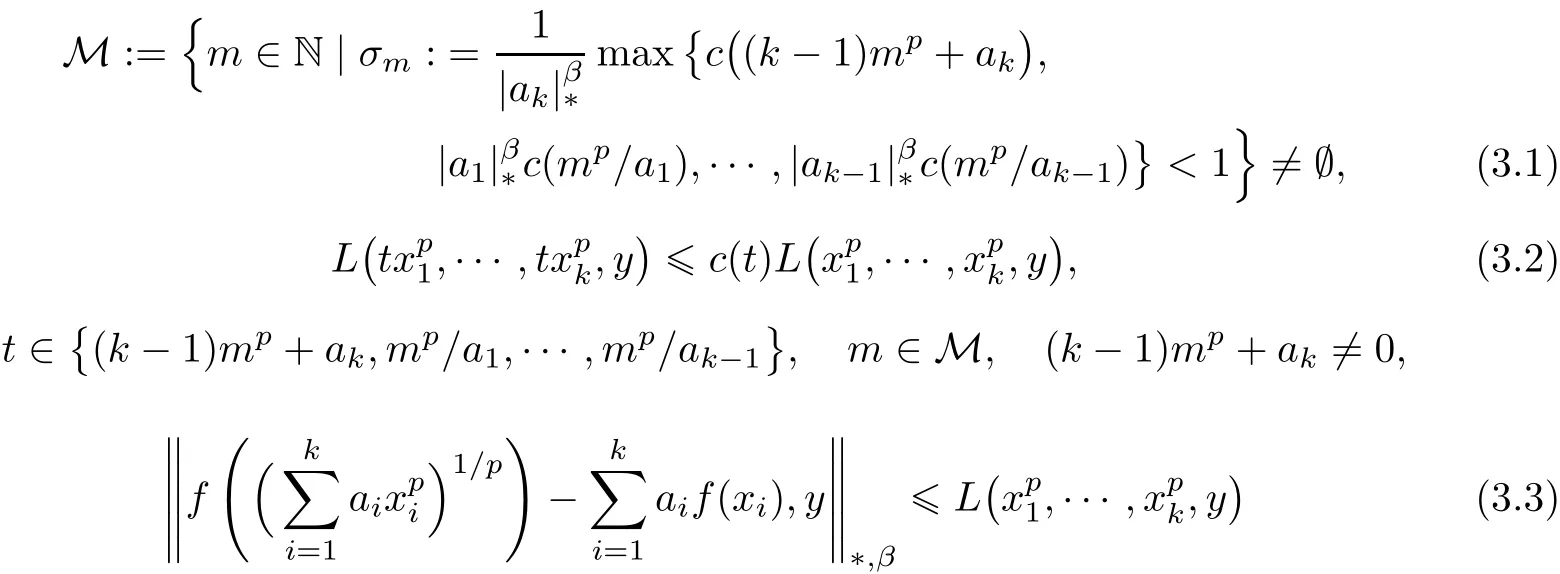
for all x1,···,xk∈ R0and y ∈ X,where f(0)=0.Then there exists a unique function Fp:R → X satisfying(1.1)for all x1,···,xk∈ R and such that

ProofFor i=1,···,k ? 1,replacing(xi,xk)byin(3.3),we get

for all x∈R0and y∈X with m∈N.For each m∈N,we de fine operator Tm:XR→XRby

Then

and inequality(3.5)takes the form

for all x∈R0,y∈X and m∈N.

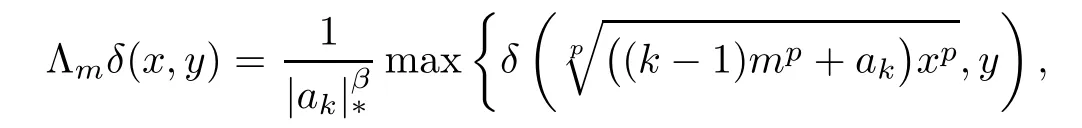
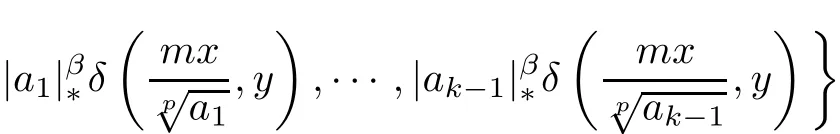
Moreover,for every ξ,μ ∈ XR0,m ∈ N,x ∈ R0and y ∈ X,we obtain

where(ξ? μ)(x)≡ ξ(x)? μ(x).So,(H4)is valid for Tmwith m ∈ N.Note that,in view of(3.2),we have

By using mathematical induction,we will show that for each x∈R and y∈X,we have

for all n∈N and m∈M.From(3.7),we obtain that inequality(3.8)holds for n=1.Next,we assume that(3.8)holds for n=r,where r∈N.Then,we have

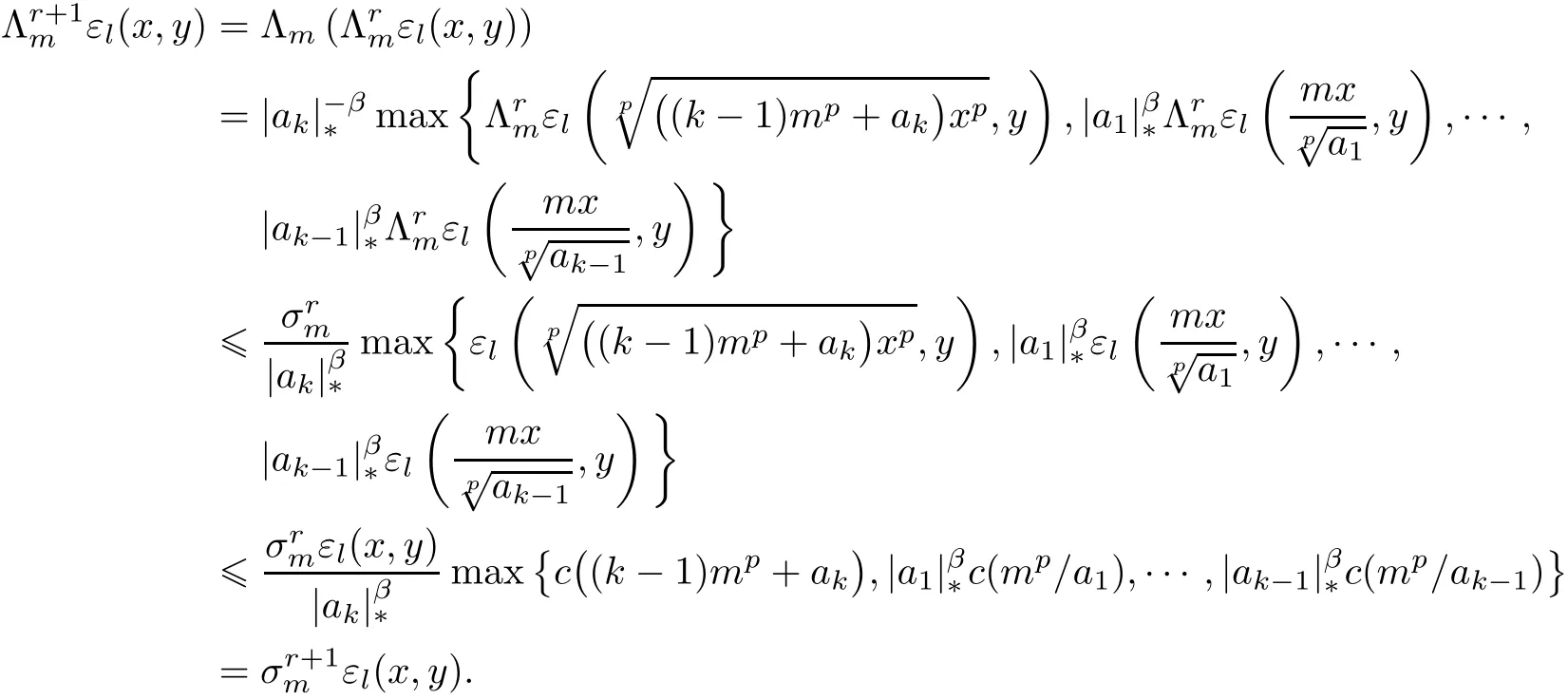
This shows that(3.8)holds for n=r+1.Now we can conclude that inequality(3.8)holds for all n∈N.Therefore,by(3.8),we obtain that

for all(x,y)∈R0×X and m∈M.Further,for each n∈N0,m∈M and(x,y)∈R0×X,we have

Consequently by Theorem 2.1(with W=R0and ? =f),for each m ∈ M the mapping:R0→X,given byfor x∈R0,is a fixed point of Tm,i.e.,

for all x∈R0and m∈M.Moreover,

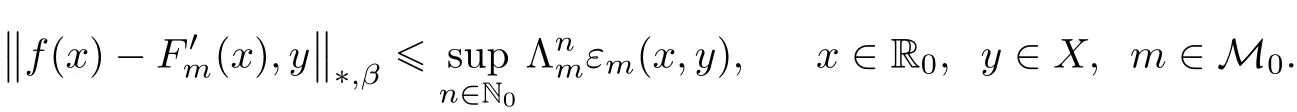
De fine Fm:R→X by Fm(0)=(0)and Fm(x)=(x)for x∈R0and m∈M.Then it is easily seen that,by(3.6),

Next,we show that

for every x1,···,xk∈ R0,y ∈ X,n ∈ N0and m ∈ M.

Clearly,if n=0,then(3.10)is simply(3.3).So, fix n∈N0and suppose that(3.10)holds for n and every x1,···,xk∈ R0and y ∈ X.Then,for every x1,···,xk∈ R0and y ∈ X,

Thus,by induction,we show that(3.10)holds for all x1,···,xk∈ R0,y ∈ X and for all n ∈ N0.Letting n→∞in(3.10),we obtain that

So,we have proved that for each m∈M there exists a function Fm:R→X satisfying(1.1)for x1,···,xk∈ R0and such that

for all x∈R0,y∈X and m∈M.

Now,we show that Fm=Flfor all m,l∈ M.So, fix m,l∈ M.Note that Flsatis fies(3.11)with m replaced by l.Hence,for i=1,···,k ? 1,takingin(3.11),we get TmF?=F?for ?=m,l and

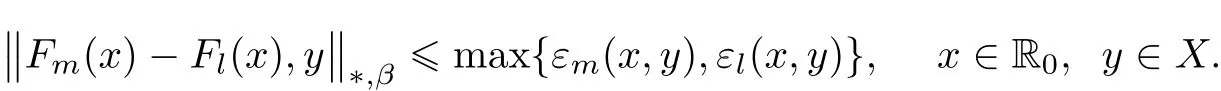
Whence,by(3.8),

for all x∈R0,y∈X and n∈N0.Letting n→∞we get Fm=Fl=:Fp,where p∈{1,2,3,4,5}.Thus,in view of(3.12),we prove that

Since(in view of(3.11))it is easy to notice that Fpis a solution to(1.1).So,we derive(3.4).

It remains to prove the statement concerning the uniqueness of Fp.So,let Gp:R→X be also a solution of(1.1)and

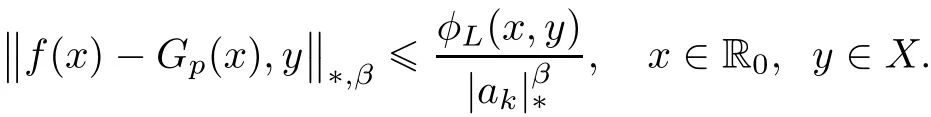
Then

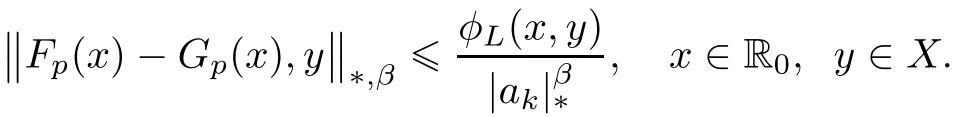
Further TmGp=Gpfor each m∈N.Consequently,with a fixed m∈M,

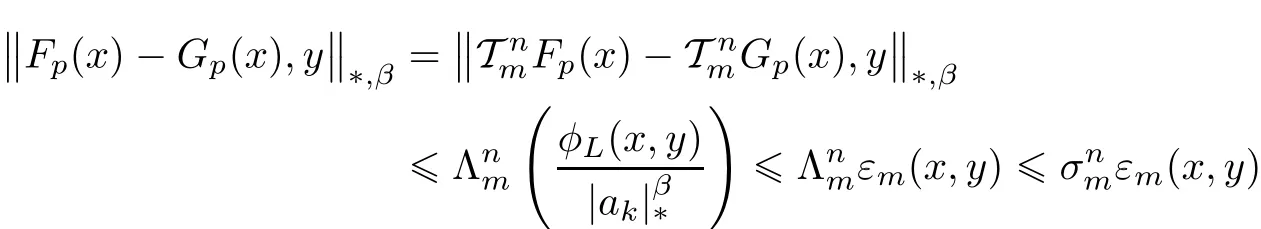
for all x∈R0,y∈X and n∈N0.Letting n→∞we get Fp=Gp.This con firms the uniqueness of Fp.The proof of Theorem 3.1 is completed. ?

The following hyperstability result can be deduced from Theorem 3.1.

Corollary 3.2Let X be a non-Archimedean(2,β)-Banach space.Let f:R → X,c:R0→R+and L:×X→R+be functions and the conditions(3.1),(3.2)and(3.3)be valid,with f(0)=0.Assume that

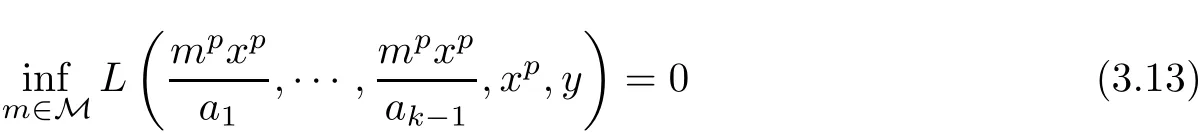
for all x ∈ R0and y∈ X.Then f satis fies(1.1)for all x1,···,xk∈ R.

Corollary 3.3Let X be a non-Archimedean(2,β)-Banach space.Let c:R0→ R+and L:×X→R+be functions and conditions(3.1),(3.2)and(3.13)be valid.Let f:R→X and F:Rk→X be two functions such that

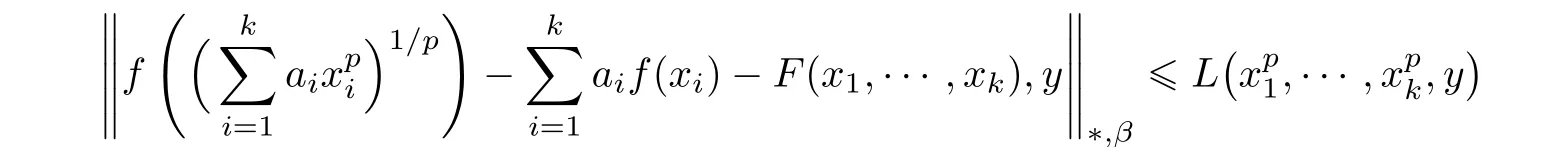
for all x1,···,xk∈ R0and y ∈ X,with f(0)=0.Assume that the functional equation

admits a solution f0:R → X for x1,···,xk∈ R0with F(0,···,0)=f0(0)=0.Then f is a solution of(3.14)for all x1,···,xk∈ R.

ProofLet g(x):=f(x)?f0(x)for x∈R.Then

It follows from Corollary 3.2 that g satis fies the functional equation(1.1)for all x1,···,xk∈ R.Therefore,

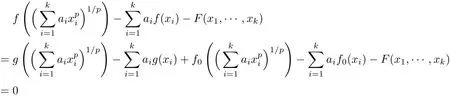
for all x1,···,xk∈ R.

4 Applications

From Theorem 3.1 and Corollaries 3.2,3.3,we derive two natural examples of functions L and c satisfying conditions(3.1)and(3.2).Namely,for

for all x1,···,xk∈ R0,y ∈ X and for some arbitrary element z ∈ X and ε,pi,s ∈ R such that,s<0 and αi>0 for i=1,···,k.

Corollary 4.1Let X be a non-Archimedean(2,β)-Banach space and ε,p1,···,pk∈ R,with ε ? 0 and.Suppose that f:R→X satis fies the inequality

for all x1,···,xk∈ R0and y ∈ X and for some arbitrary element z∈ X,where f(0)=0.Then the following two statements are valid.

ProofLetandin Theorem 3.1 for all x1,···,xk∈ R0and y ∈ X and for some arbitrary element z ∈ X,where t∈ R0and p1,···,pk,ε∈ R such that ε? 0 and,then we get that condition(3.2)is valid.Obviously,(3.13)holds ifand.On the other hand,we have

So we obtain(3.1),as well.Then,by Theorem 3.1 and Corollary 3.2,we get the desired results.?

Corollary 4.2Let X be a non-Archimedean(2,β)-Banach space and ε,p1,···,pk∈ R,such thatand.Let f:R→X and F:Rk→X be two functions such that

for all x1,···,xk∈ R0and y ∈ X and for some arbitrary element z ∈ X,where f(0)=0.Assume that the functional equation

admits a solution g0:R → X for x1,···,xk∈ R0with g0(0)=F(0,···,0)=0.Then f is a solution of(4.1)for all x1,···,xk∈ R.

Corollary 4.3Let X be a non-Archimedean(2,β)-Banach space and ε,s,αi∈ R such that ε? 0,s<0 and αi>0 for i=1,···,k.Suppose that f:R → X satis fies the inequality

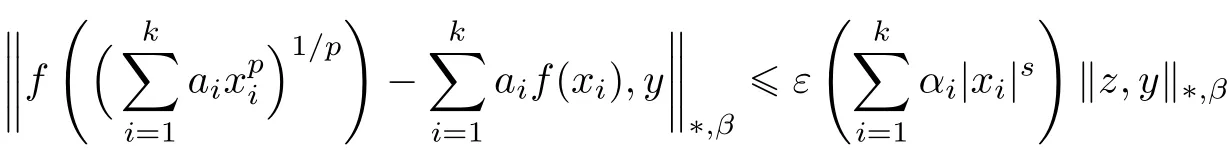
for all x1,···,xk∈ R0and y∈ X and for some arbitrary element z∈ X,where f(0)=0.Then there exists a unique function Fp:R → X satisfying(1.1)for all x1,···,xk∈ R and such that

for all x∈R0,y∈X and for some arbitrary element z∈X.

ProofLetand c(t)=|t|s/pin Theorem 3.1 for all x1,···,xk∈ R0and y ∈ X and for some arbitrary element z ∈ X,where t∈ R0and ε,αi,s ∈ R such that s<0,αi>0 and ε? 0 for i ∈ {0,1,2,···,k}.Then we get that the condition(3.2)is valid.Obviously,

On the other hand,we have

Thus,there exists m0∈N such that

So we obtain(3.1),as well.Then,by Theorem 3.1,we get the desired results.