Ji-Lin You (游擊林) Qing-Dong Wu (吳慶東) Xiao-Ping Zhang (張小平) and Qi-Jun Zhi (支啟軍)?

1School of Physics and Electronic Sciences, Guizhou Normal University, Guiyang 550001, China

2Guizhou Provincial Key Laboratory of Radio Astronomy and Data Processing, Guizhou Normal University,Guiyang 550001, China

3State Key Laboratory of Lunar and Planetary Sciences, Macau University of Science and Technology, Macau 999078,China

(Received September 13, 2018; revised manuscript received October 11, 2018)

Abstract We have systematically analyzed the experimental β?-decay half-lives of waiting point heavy nuclei around neutron number N=126.A new set of parameters for the exponential formula of β?-decay half-lives is proposed.The forbidden transition effects are included in the new set of parameters self-consistently.Theoretical β?-decay half-lives of nuclei around N=126 are compared with recent theoretical results and experimental data.It is found that the new theoretical results are in better agreement with experimental data.The unknown β?-decay half-lives of some nuclei in this region are predicted for studies on nuclear structure far from stability and the nucleosynthesis in stars.

Key words: β?-decay half-lives, waiting point nuclei, nucleosynthesis

1 Introduction

Theβ-decay half life is one of the most important weak interaction reaction rates.It is of great significance for not only nuclear structure research, but also for astrophysics.[1?5]From astrophysical point of view, theβ-decay half-lives are much important for nuclei synthesis (thus star elements abundance)and evolution of stars.It is the competition betweenβ-decay rates and neutron capture rates that determines by which ways (rapid neutron capture process (rprocess)or the slow neutron capture process(sprocess))the heavier nuclei in universe are produced.Forrprocess, in which theβ-decay rates is smaller than the neutron capture rates, seed nuclei can capture a neutron and hence make heavier nuclei before they decay byβ-transition.It is believed that half of the neutron-rich atomic nuclei heavier than iron are made by therprocess.Nucleus lighter than Fe is produced though thermonuclear reactions.Now, it is generally accepted thatrprocess occurs in these environment, high temperature and high neutron density, although the actual site ofr-process is hard to be determined.[6?8]Under these conditions, neutron captures are dominant in comparison withβ-decays,and ther-process path moves along a chain of extreme neutron-rich nuclei.Along these paths, the so called waiting point nuclei with magic numberN= 50,82,and 126 are of great interest because the large neutron separation energies of these nuclei maker-process matter flow slow down when it reaches these neutron magic nuclei.It waits for someβ-decays to occur before further neutron captures are possible.The mass flow are carried to heavier nuclei and consequently the matter is gathered,which leads to the so called peaks in abundance distribution ofr-process.Thus, theβ-decay half-lives of the waiting point nuclei are very important because it is the key to understand the thirdr-process peak of heavy nuclei with mass numbersA ～200.From the point of view of nuclear science,β-decay half-lives of waiting point nuclei are also of great importance, because the decay rates are mainly determined by theQvalues and the transition matrix elements, which are strongly affected by the nuclear structures and thus are very important quantity for nuclear structure study, especially the shell structure far from stability.

Despite their importance for astrophysics and nuclear physics,a few experimental data of half-lives are obtained only for waiting point nuclei withN= 50 and 82.[3,9?11]ForN= 126, experimental data are very absent.Thus,for astrophysicalr-process simulations, the needed halflives only rely on theoretical estimates.The situation of half-lives for nuclear structure study is also the same.Therefore, theoretical calculations of half-lives are very important.Since Fermi[12]first proposedβ-decays theory in the 1930s, many scientists have done a lot of theoretical research on the calculation ofβ-decay half-lives.Because theQ-values are much low, these studies have considered mainly on allowed transitions.The Quasiparticle Random Phase Approximation (QRPA)either on top of semi-empirical global models[13?16]or the Hartree-Fock-Bogoliubov method or the shell model is applied to these calculations, which reproduces well the experimental half-lives of waiting point nuclei inr-process.[17?19]The calculations can give a reasonable account of the few experimental data, however, some of these microscopic calculations are time-consuming and model dependent.Therefore, besides the microscopic calculations, there exist other phenomenological methods.Sargent[20]proposed a law that theβ-decay half-lives is proportional to the fifth power ofβ-decay energies (T1/2∝E5).Recently, we analyzed the experimental data of nuclearβ-decay half-lives and found an exponential law ofβ-decay half-lives for nuclei far from stability,which was similar to the relation betweenα-decay half-lives andα-decay energies.[21?23]The results calculated with an empirical formula based on this exponential law reproduce the experimental data.

Very recently, the forbidden transitions are included in the QRPA and the shell model calculations.The first forbidden transitions are considered and half-lives are calculated for waiting point nuclei around neutron numberN= 50, 82, and 126.[24?25]It was pointed out that the forbidden transitions become very important and must be considered for waiting point nuclei aroundN= 126.As we know,the available experimental data aroundN=126 are very poor.In addition, microscopic calculations including forbidden transitions are very time-consuming.Therefore, it is of great importance to give another theoretical calculations of the waiting point nuclei aroundN= 126.In this paper, we will re-exam the formulae in the literature[22]by taking into account the forbidden transitions and the shell effects with the aim to give better description ofβ-decay half-lives for waiting point nuclei aroundN= 126, which are very useful for nuclear structures and the third peak elements production in stars.

The paper is organized in the following way.In Sec.2,we propose a new set of parameters for empirical formula for calculating theβ?-decay.In Sec.3, we utilize the formula to calculate half-lives ofβ?-decays, and to predict theβ?-decay half-lives of waiting point nuclei aroundN=126.A summary is given in Sec.4.

2 The Theoretical Formula

Zhanget al.[21?22]systematically analyzed the experimentβ-decay half-lives of nuclei and discovered an exponential relationship betweenβ?-decay half-lives (in log10scale)and the nucleon numbers of parent nuclei.They proposed an exponential formula to calculate theβ-decay half-lives of nuclei far from stability:

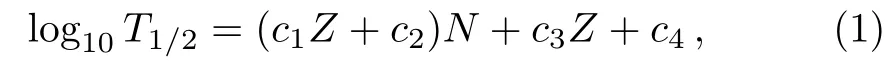
whereT1/2isβ?-decay half-life (in seconds)andZis the proton number of parent nucleus.By a least-squares fit,the values ofc1,c2,c3andc4are: 2.65×10?4,?0.2275,0.3652, and?0.8852, respectively.[22]If the shell effects are included, the formula has the form:

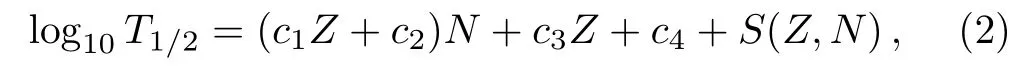
whereS(Z,N)is a term of shell effect correction and can be written as:

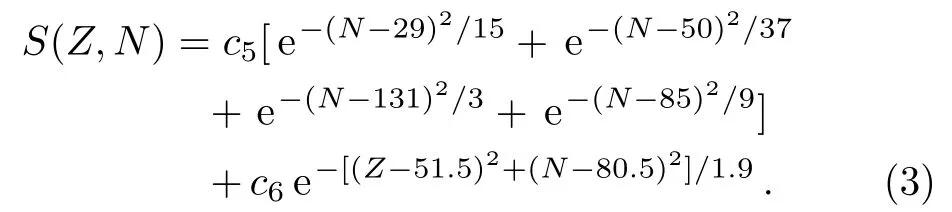
Zhanget al.[22]have tested the accuracy and reliability of the two formulae.For the chosen center ofN=131 in the Gaussian function in Eq.(3), Zhanget al.has given an explanation.[22]On the one hand,β?-decay half-lives depend on the decay energies, which are affected by the shell effects near proton or neutron “magic number”.On the other hand,theβ?-decay half-lives also depend on the energy level structure of the parent and daughter nuclei.According to the selection rule forβ-transitions, forbidden transition plays an important role near the region of proton or neutron “magic number”.The superposition of these two effects causes the deviation of the Gaussian center fromN= 126.It is interesting to see from the data that a bigger correction is needed nearN=131, instead ofN= 126.As pointed out in Refs.[24–25] that the contributions of forbidden transitions, which were not fully considered by a global fit in Ref.[22], are large and must be considered separately for nuclei aroundN=126.Therefore,we re-examine Eq.(2)and write it in the form:

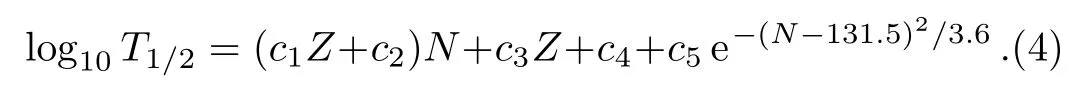
By a least-squares fit to the available experimental data of 27 nuclei withZ=73–83,N=117–136,we obtain a new set of parameters:c1=?0.002 87,c2= 0.041 88,c3= 0.785 26,c4=?37.1312 andc5= 0.635 56, respectively.Here, the Gaussian centerN= 131.5 in Eq.(4)is a little bit different from the center ofN= 131 in Eq.(3).The reason is that the fit for Eq.(3)is a global fit from light nuclei to heavy nuclei, while the parameters for Eq.(4)are obtained from a local fit aroundN=126.Because the fit is mainly concentrated on nuclei aroundN=126,the forbidden transitions are described more accurately in the new set of parameters.In the following,we will test the reliability of this new set of parameters, and use Eq.(4)with its new parameters to calculate and predict the half-lives of neutron-rich nuclei aroundN=126,which is important forrprocess.

3 Results for β?-Decay Half-Lives of Nuclei around N= 126

In Table 1,we compared calculated results from Eq.(4)with experimental data.Theoretical results from Eqs.(1)–(2)and from FRDM model are also listed for comparison.From Table 1,one can see that the calculated results from Eqs.(1)–(2)with old parameters have larger deviations from experimental data.For example, the deviation of190Ta is about 5 times with old parameters for Eq.(1).However,calculatedβ?-decay half-lives from Eq.(4)with the new set of parameters agree with experimental data quite well.It can be seen in Table 1 that, the calculated results of Eq.(4)are much closer to the experimental data when compared with the FRDM model with or without forbidden transitions.These show that the influence of forbidden transitions are very important and must be considered for nuclei aroundN=126.

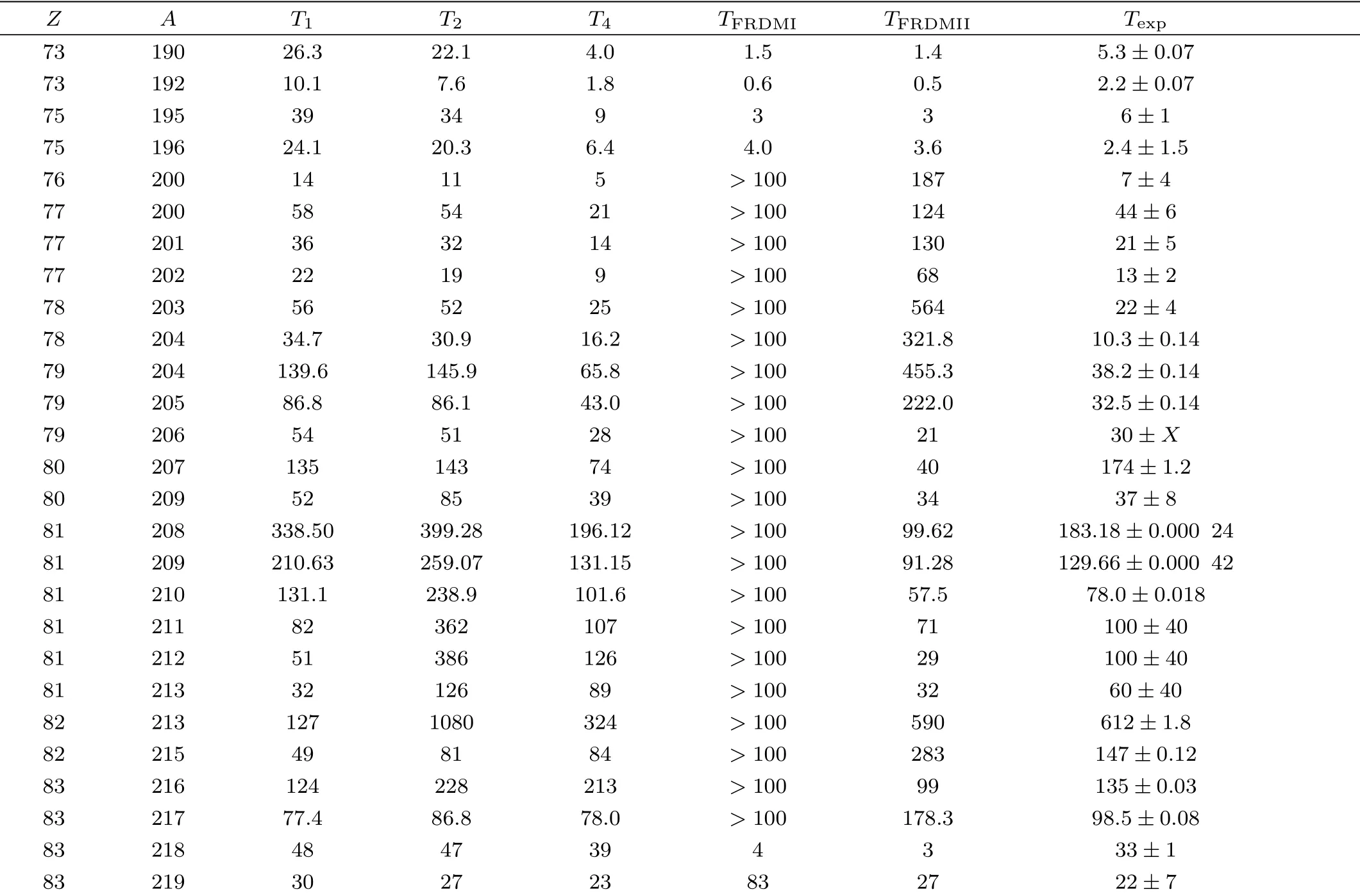
Table 1 β?-decay half-lives (in seconds)for nuclei with Z= 73–83 and N= 117–136 from calculated and experimental results.The first column and second column represent the proton number and mass number of a parent nucleus, respectively.Calculated half-lives from Eq.(1)and Eq.(2)with old parameters[22] are represented as T1 and T2 in column 3 and column 4, respectively. T4 in column 5 represents the theoretical values from Eq.(4)with the new set of parameters. TFRDMI and TFRDMII in the sixth and seventh columns represent theoretical values from FRDM model without and with contributions of forbidden transitions, respectively.[15?16] The last column represents experimental data.[26] The symbol X represents unknown error bar.

In Figs.1 and 2,the logarithms of the ratios between calculated values and experimental ones are plotted versus the proton and neutron numbers of parent nuclei for various models and formulae.In the two figure, it can be seen that theoretical value from Eqs.(1)–(2)are larger than experimental data for the smallerZandNin general.Theoretical resultsTFRDMIIfrom FRDM model have the largest deviations from experimental data, while resultsT4from Eq.(4)with the new set of parameters have the smallest deviations.For example, the largest deviation is about 32 times forTFRDMII, but the deviations ofT4are less than 5 times, which shows that the new formula Eq.(4)can give good description of theβ?-decay half-lives of nuclei aroundN=126 region where the contribution of forbidden transitions are important.

Based on the above formulae, we calculated the half-lives of 76 nuclei withZ= 73–82 andN= 121–139 for both nuclear and astrophysical purposes.The results together with theoretical calculations from FRDM models with and without forbidden transitions are listed in Table 2.It is clear seen that the calculated results with forbidden transitions are smaller than those without forbidden transitions, which shows the importance of forbidden transitions.It can bee seen in Table 2 that, in general, results from two models have small deviations and in general our results are smaller than the FRDM model results.More experimental data in future could be valuable to verify the predictions from different models.

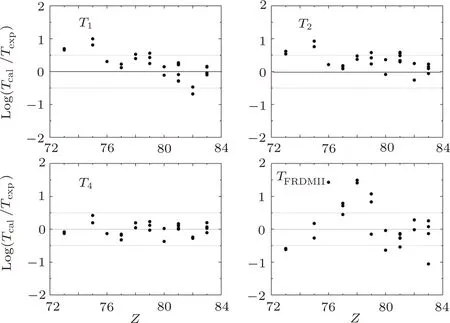
Fig.1 The logarithms of the ratios between calculated values from T1 (Eq.(1)with old parameters), T2 (Eq.(2)with old parameters), T4 (Eq.(4)with new parameters), and TFRDMII and experimental ones plotted versus the proton numbers of parent nuclei with Z=73–83.Experimental data are taken from Ref.[26].

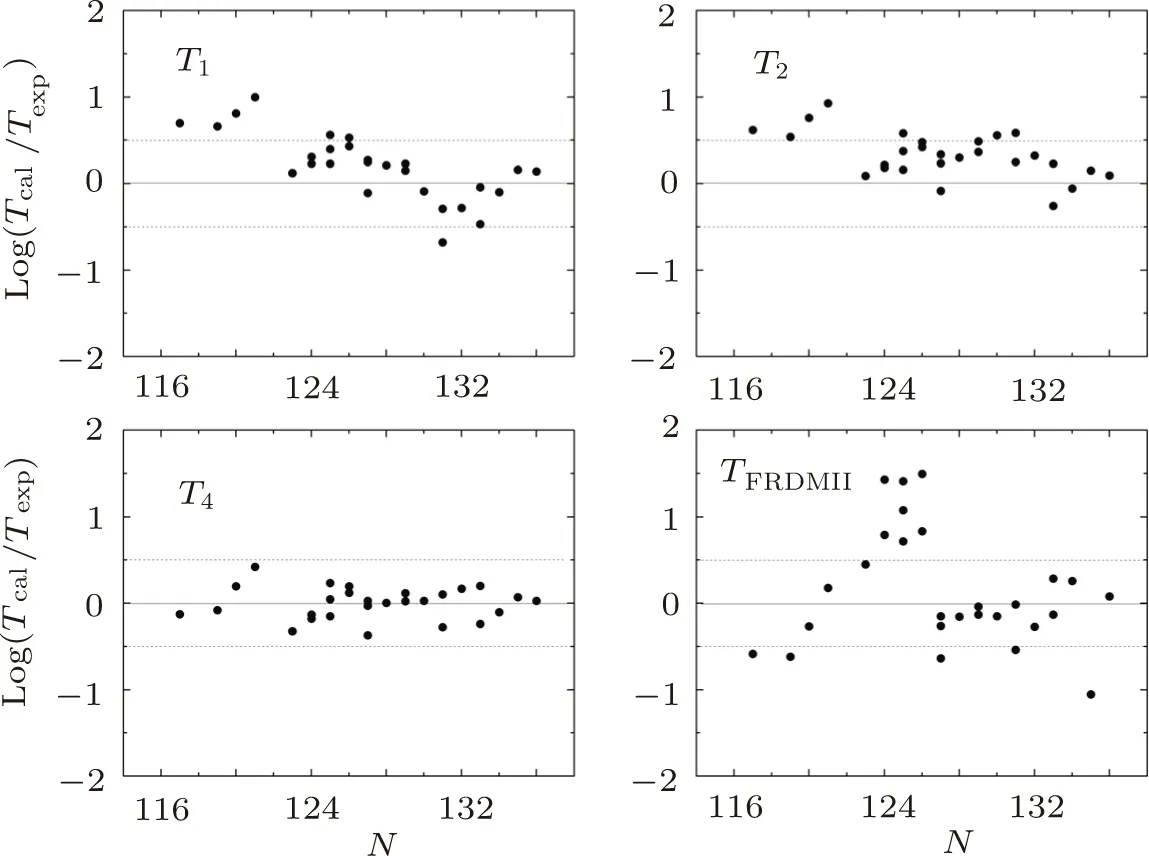
Fig.2 The same as Fig.1, but the results plotted versus N.

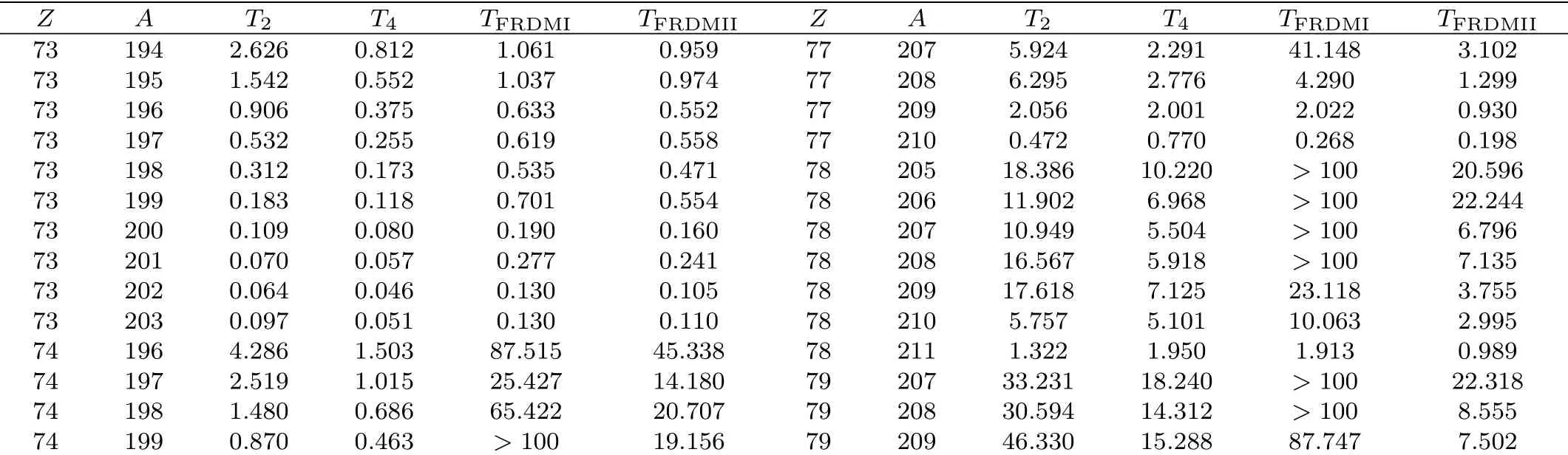
Table 2 Predicted β?-decay half-lives (in seconds)for nuclei with Z=73–82 and N=121–139.The first column and second column represent the proton number and mass number of a parent nucleus, respectively.Calculated half-lives from Eq.(2)with old parameters[22] are represented as T2 in column 3. T4 in column 4 represents the theoretical values from Eq.(4)with the new set of parameters. TFRDMI and TFRDMII in the fifth and sixth columns represent theoretical values from FRDM model without and with contributions of forbidden transitions, respectively.[15?16]

Table 2 (continued)

4 Summary

In summary, by considering the contributions of forbidden transitions, theβ?-decay half-lives for nuclei aroundN= 126 are studied and a new set of parameters for the exponential law have been proposed.With the new set of parameters,theβ?-half-lives of 27 nuclei for nuclei withZ=73?83 are calculated and compared with other theoretical results and experimental data.It is found that theoretical results considering the forbidden transitions agree well with experimental data.Meanwhile, we predict theβ?-half-lives of some unknown neutron-rich nuclei aroundN=126 for future nuclear and astrophysical study, especially forrprocess nucleosynthesis in stars.