L.Bruno Chandrasekar?M.Karunakaran and K.Gnanasekar

1Department of Physics, The American College, Madurai 625002, India

2Department of Physics, Alagappa Govt.Arts College, Karaikudi 630003, India

(Received August 10, 2018; revised manuscript received September 21, 2018)

Abstract Using the matrix method, spin-dependent tunneling properties such as barrier transparency, the degree of resonance polarization, and tunneling lifetime of electrons are examined in the non-magnetic/diluted magnetic semiconductor heterostructure.The effects of the double δ-potential and the magnetic field are discussed on the transport properties of the electrons.The introduction of double δ-potential shifts the resonance peak of polarization to the higher energy value.Both height and position of the δ-potential influence the degree of resonance polarization in the considered heterostructure.The increasing magnetic field enhances the spin-polarization.

Key words: matrix method, heterostructure, δ-potential

1 Introduction

Spin-transport properties in low dimensional systems have been attracted worldwide due to its technological important applications such as spin-quantum computers and spin-transistors.[1?2]Moreover, the basic physical characteristics of spin-dependent charge carriers through the heterostructures such as Hartmann effect, dwell time, spinflip scattering, BGKC observation and delay time encourage this research.[3?6]The effective spin injection in semiconductors is still a challenge out of few.Spin injection in semiconductor from a ferromagnetic conductor is one of the choices for the effective injection.But the growth of ferromagnetic conductor on semiconductor and the conductivity mismatch leads the research community to find another possibility.Later, the spin injection from the semiconductor to the semiconductor is proposed.After the proposal given by von Ortenberg, Mn-based superlattices are examined by various research groups.[7?12]

Pappet al.reported the spin-dependent tunneling of electrons in asymmetrical heterostructures using transfer matrix method.In the multilayer heterostructure ZnSe/Zn1?yBeySe/ZnSe/ZnxMn1?xSe sharp resonance peaks for spin-up electrons and suppressed transmission for spin-down electrons are observed with zero bias, whereas in ZnSe/Zn1?zCdzSe/ZnSe/ZnxMn1?xSe heterostructures wide resonance peaks for spin-down electrons and suppression for spin-up electrons are observed.These structures with the suitable fields are proposed for spin filter and spin diode.[13]Saffarzadehet al.analyzed the effect of bias voltage and barrier thickness in ZnSe/Zn1?xMnxSe symmetrical and asymmetrical heterostructures.The transmission coefficients for the electron energies,which are near the Fermi energy increase as the bias voltage increases.The current density for spin-up electrons increases when the thickness of the non-magnetic ZnSe layer increases.Moreover, the current density for spin-up electrons in the asymmetrical heterostructure is higher than the symmetrical one, but for the spin-down electrons, it does not change considerably.[14]Gnanasekaret al.reported the effect of induced-Rashba due to the external electric field in ZnSe/Zn1?xMnxSe double-barrier heterostructure.The spin-up electrons are completely blocked and spin-down electrons are almost transmitted when the CBO is either zero or positive values.Four times enhanced current density is also observed in the heterostructure when the electric field induced Rashba is accounted.[15]

Minget al.examined the ballistic transport of electrons through ZnMnSe/ZnSe/ZnBeSe heterostructures.The negative differential conductance in the triple barrier heterostructure is observed, and it disappears when the bias voltage is large.Moreover, the polarization rate exhibits high values of the degree of spin polarization.[17]

This paper reports the effect of magnetic field andδ-potential on the spin-transport in ZnSe/Zn1?xMnxSe symmetrical double-barrier heterostructure.The effect ofδ-potential in non-magnetic semiconductor heterostructure is reported in the literature.[18?20]But from our best of knowledge, the effect ofδ-potential on spintransport in non-magnetic/diluted magnetic semiconductor heterostructure with the magnetic field is not available.This induces us to find the barrier transparency,polarization efficiency, and tunneling time of electrons in ZnSe/Zn1?xMnxSe heterostructure with doubleδpotential as a function of the height of theδ-potential and its position.The theory and the formalism are given in Sec.2.The observed results and the discussions are in Sec.3 followed by the conclusion.

2 Theory and Formalism

We consider spin-dependent electrons tunneling through double paramagnetic barriers with the external magnetic field.It is assumed that the magnetic field is applied along the motion of the incident electrons, i.e.,along thez-direction.

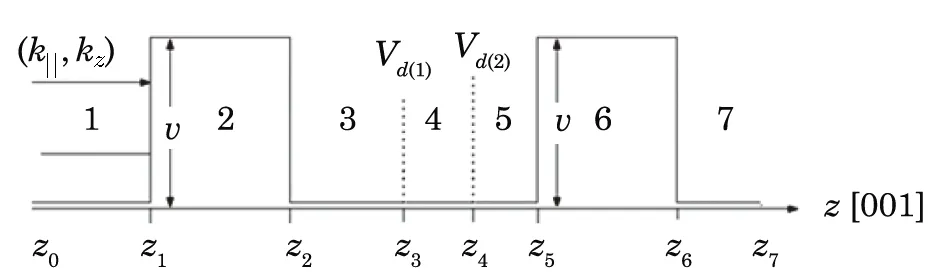
Fig.1 Representation of heterostructure.

The effective Hamiltonian of the system can be written as

wherePis the momentum operator,Ais the vector potential,mis the electron effective mass,HDis the Hamiltonian corresponds to Dresselhaus spin-orbit interaction andVeff(B,z)is the effective potential of the barriers with external field.The Dresselhaus Hamiltonian is

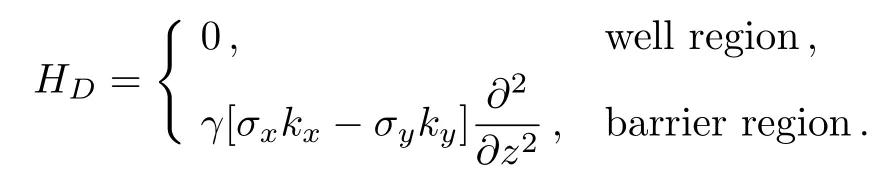
The effective potential of the heterostructure when the external field is applied is given asVeff(B,z)=V0(z)+Vz(B)+VGZ(B).Since the paramagnetic barrier considered here is Zn1?xMnxSe, the giant Zeeman effect is also accounted in this work.This is because of the sp-d interaction between the spin of the injected electrons and spin of 3d electrons in Mn ions.The potential in the heterostructure is given as

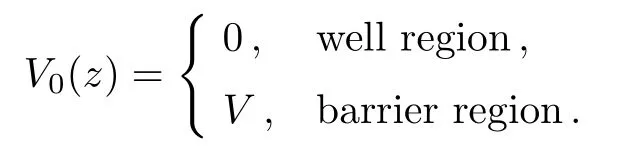
VZ(B)is the Zeeman splitting andVGZ(B)is the giant Zeeman splitting and is given as, respectively, (1/2)gμσBand(?1/2)N0αxeff﹤Sz﹥σ[Θ(zj)Θ(a?zj)+Θ(zj ?a?(b+c+d))Θ(a+(b+c+d)+e ?zj)].Here, Θ(z)Heaviside function,σis +1 for spin-up electrons and?1 for spin down electrons, “g” is the effective Landegfactor,μBis the Bohr magenton,N0αis the electronic sp-d exchange constants in the diluted magnetic semiconductors,xeffis the effective “Mn” concentrations and﹤Sz﹥is the thermal average of the z-component of the Mn2+spin.[15]TheSzis found from the expression

whereTeff=T+T0.The electron wave function in the different regions is given as

As if these things were of any consequence! Why did he not leave them alone? Who would trouble themselves about such trifles? especially at a comedy, where every one is expected to be amused

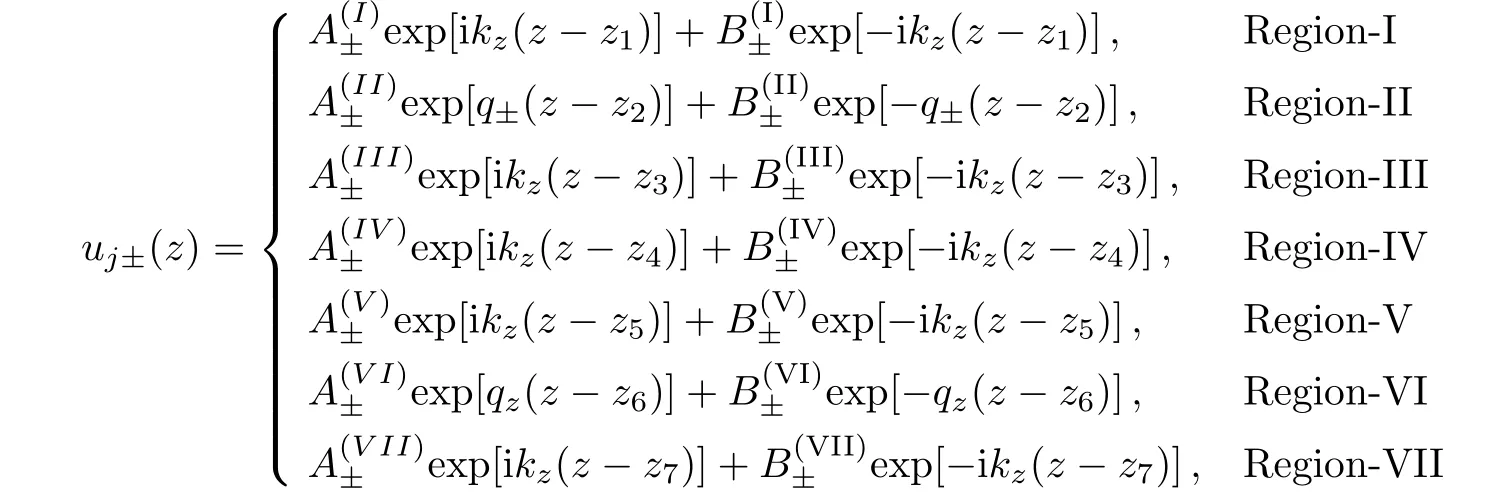
wherekz,q±are the wave vectors in the well region and the barrier region, respectively.The wave vectors are given as

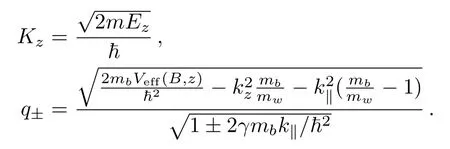
The spin-dependent bounday conditions are[21]

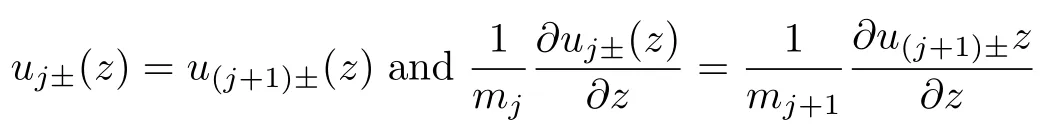
forj=1,2,5,6,

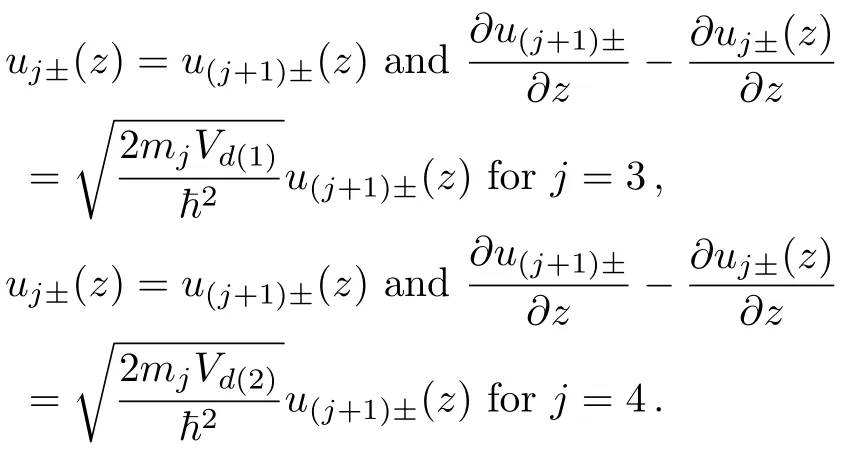
According to the boundary conditions, the coefficients are related as

Mjis the interface matrix in thejthregion.the transfer matrix is

The transmission coefficient of electroncs in the heterostructures isThe polarization efficiency of the transmited electrons can be written as

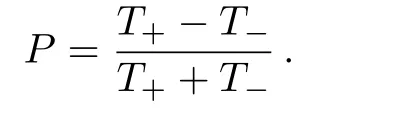
The full-width at half maximum of the barrier transparency peaks are found and the tunneling life time of spin-dependent electrons are calculated using the Heisenberg’s uncertainty principle.

3 Results and Discussions

ZnSe/Zn1?xMnxSe double barrier heterostructure is considered with identical barriers in terms of barrier width and barrier height.The parameters used in this work are listed:m?= 0.16m0,V= 0 meV,a=d= 15 nm,N0α= 0.26 eV,x= 0.05,xeff= [x(1?x)]12,T= 4.2 K,T0=1.7 K, andg=1.1.[10]

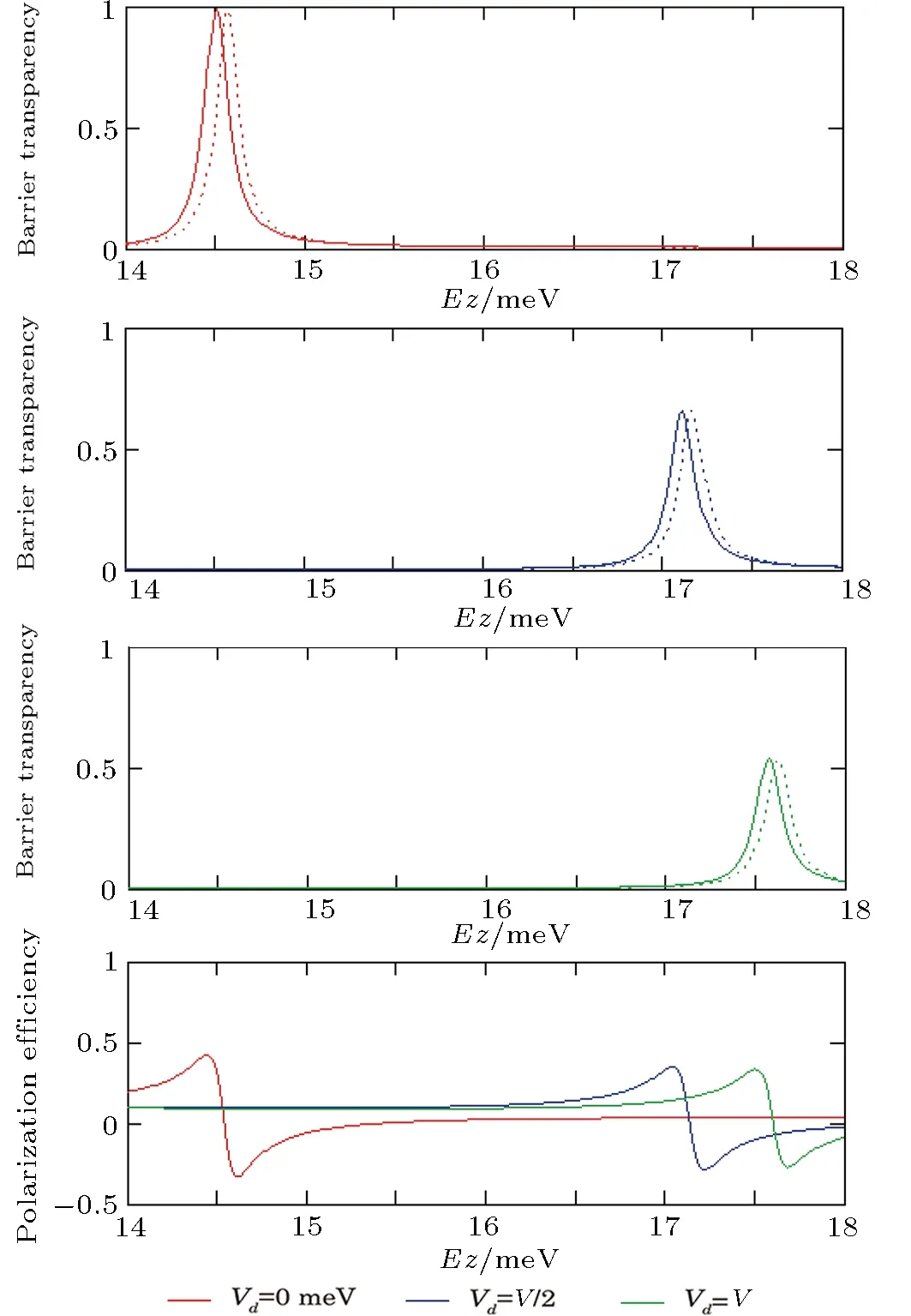
Fig.2 Barrier transparency and polarization efficiency for various height of delta potential.

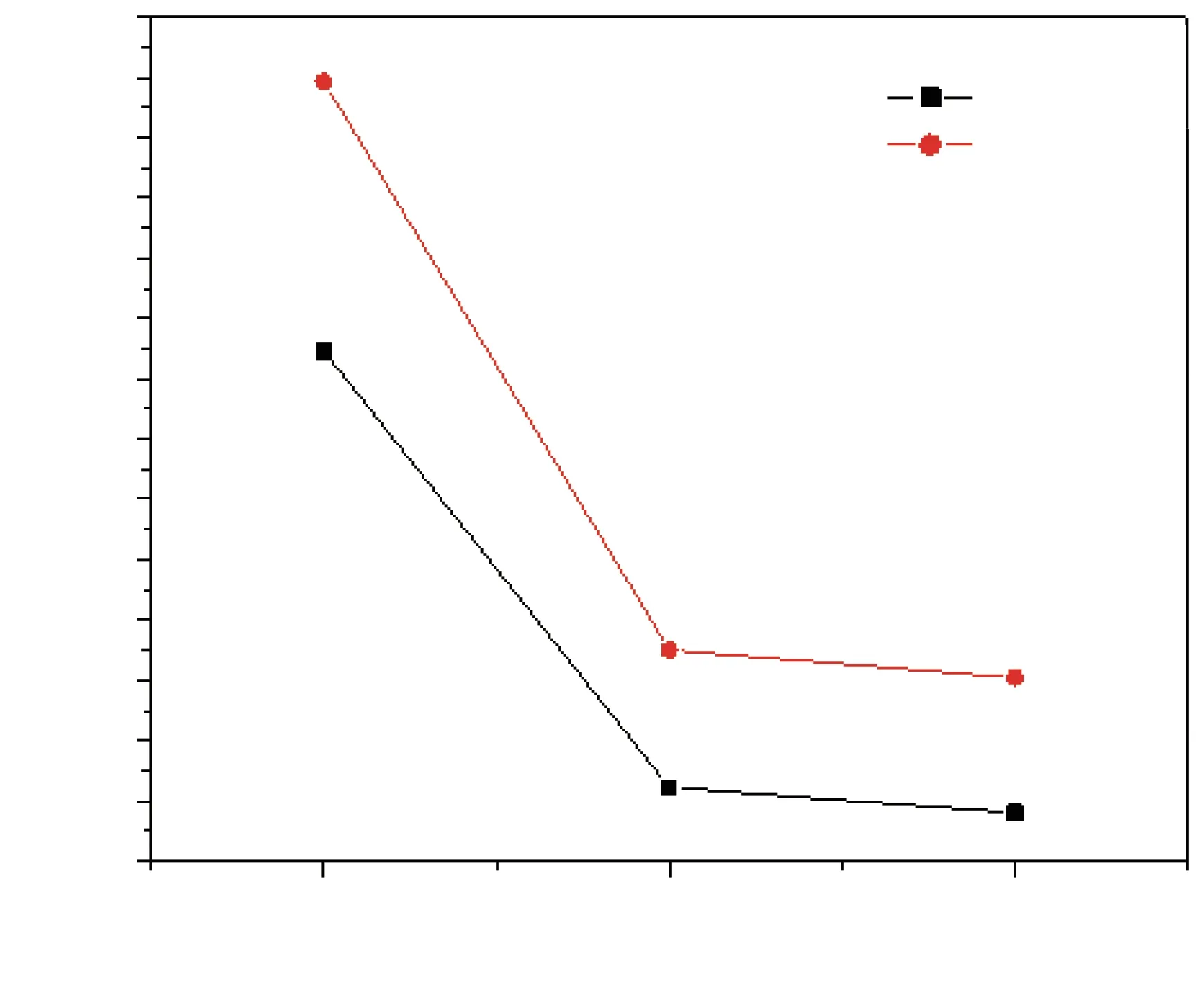
Fig.3 Tunneling lifetime of electrons for various δ-potential.

Figure 2 shows the barrier transparency (continuous line represents the spin-up transparency and dotted line represents spin-down transparency)and polarization efficiency for various height of the delta potential.The height of the barrier transparency peaks,the energy of resonance polarization and polarization efficiency strongly depends on the height of the delta barrier.As mentioned above, it is assumed that the height of both the barriers is identical.The transmission of electrons through the heterostructure is highly suppressed as the height of the delta potential increases.Moreover, it is observed that the transparency peak shifts to the high value on the energy scale.As the degree of resonance polarization is maximum when there is no delta potentials are present in the well region and the degree of resonance polarization decreases as the height of the delta potential increases.Luet al.reported the role of the height of single delta potential in InAs/GaAs double-barrier heterostructure with the in-plane magnetic field.Our results about the effect of the height of the delta potential are in agreement with the results presented by Lu.[18]

The introduction of theδ-potential in the nonmagnetic semiconductor/diluted magnetic semiconductor heterostructure influences the tunneling lifetime of the charge carriers.Exactly speaking, the introduction of theδ-potential reduces the tunneling lifetime of electrons in the ZnSe/Zn1?xMnxSe heterostructure, whereas it is almost the same in the case of non-magnetic semiconductor heterostructure.[20]Figure 3 shows the variation of tunneling lifetime as a function of the height of theδ-potential.Now, we have no other reports to compare the role ofδ-potential on tunneling lifetime between nonmagnetic semiconductor/diluted magnetic semiconductor heterostructure, it needs further investigations.

Figure 4 shows the barrier transparency and polarization efficiency of electrons for various positions of the delta barriers.As the delta barrier approaches each other, that is the distance between delta barriers decreases from 3 nm to 1 nm, the barrier transparency peaks shifts to the lower energy of incident electrons.The most notable point is that the barrier transparency becomes shaper and it is enhanced as the barrier approaches each other.Moreover,the polarization efficiency of electrons highly depends on the distance between the delta barriers.One can obtain the high polarization efficiency when the distance between the delta barriers is very small.As theδ-potential approaches each other, the tunneling lifetime of electrons decreases linearly and is shown in Fig.5.

The application of the magnetic field increases the effective potential of the heterostructure due to the giant Zeeman effect.The barrier transparency and the polarization as a function of the applied magnetic field are given in Fig.6.

Fig.4 Barrier transparency and polarization efficiency for various position of delta potential.

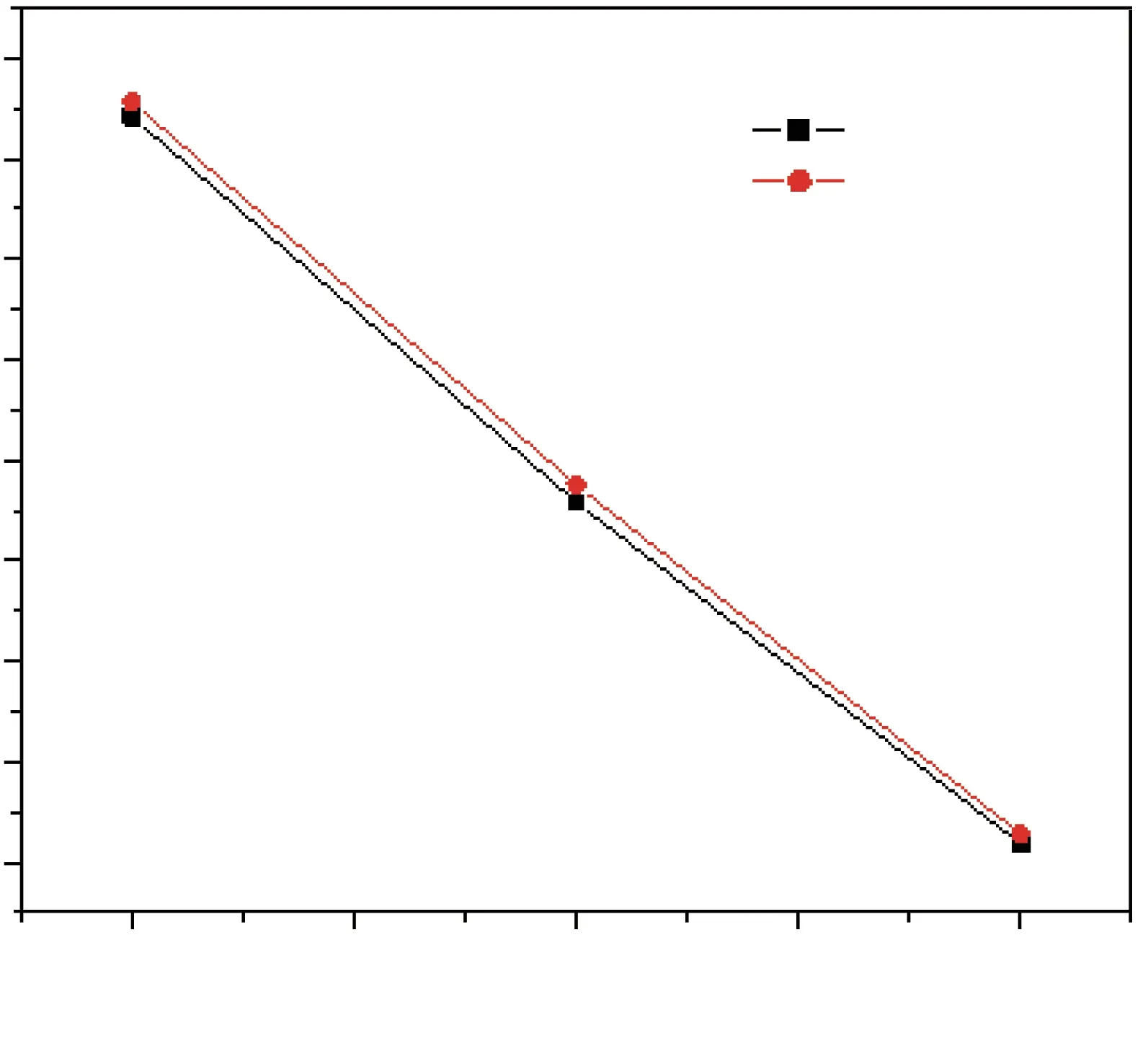
Fig.5 Tunneling lifetime of electrons for various distances between delta potentials.

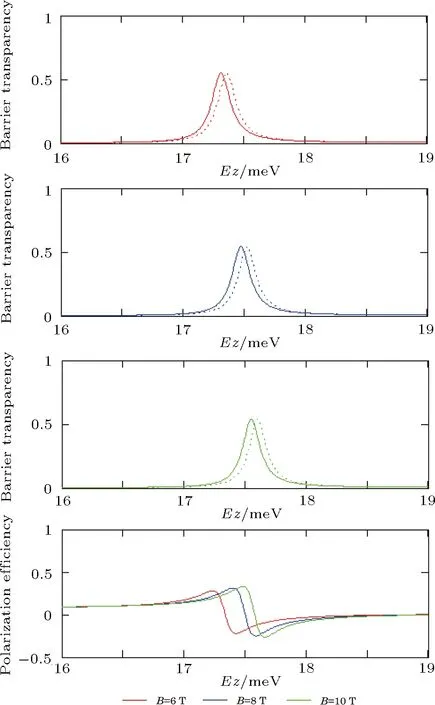
Fig.6 Barrier transparency and polarization efficiency for various magnetic fields.

The increasing magnetic field shifts to the resonance energy to the higher energy.Moreover, the enhanced polarization efficiency is achieved due to the high magnetic field.The tunneling lifetime of spin-up electrons is 3.528 ps and for spin-down electrons is 3.586 ps, when the applied field is 6 T.From these numerical values, it is observed that the tunneling time of spin-down electrons are higher than spin-up electrons.But the difference is very small.The tunneling of spin-electrons increases as the magnetic field increases.When the applied field is high,the effective potential increases due to the enhancement of Zeeman and giant Zeeman effect.Hence the tunneling lifetime of electrons is also increased,but the variation is very small.This is in agreement with the reported results.[22]

In short, the degree of resonance polarization (i)decreases as the height of the delta increases, (ii)increases as the distance between the delta potential decreases and(iii)increases as the magnetic field increases.

4 Conclusion

The spin-dependent transport properties are reported using the transfer matrix method.Suppressed barrier transparency is observed due to the introduction of theδ-potential and it leads to the reduced polarization efficiency.High polarization efficiency is achieved when the distance betweenδ-potential is minimum.The tunneling lifetime of the electrons highly is influenced by theδ-potentials.These results can be useful for the fabrication of spin-based devices.