Dan Wen(文丹),Kai Lin(林凱),and Wei-Liang Qian(錢衛(wèi)良),3,?

1Faculdade de Engenharia de Guaratinguetá,Universidade Estadual Paulista,12516-410,Guaratinguetá,SP,Brazil

2Hubei Subsurface Multi-Scale Imaging Key Laboratory,Institute of Geophysics and Geoinformatics,China University of Geosciences,Wuhan 430074,China

3Escola de Engenharia de Lorena,Universidade de S?o Paulo,12602-810,Lorena,SP,Brazil

AbstractIn this work,we study the scalar quasinormal modes of a planar black hole metric in asymptotic anti-de Sitter spacetime derived from a particular Lovelock theory.The quasinormal frequencies are evaluated by adopting the Horowitz-Hubeny method as well as a matrix formalism.Also,the temporal evolution of small perturbations is studied by using finite difference method.The roles of the dimension of the spacetime,the parameter of the metric k,as well as the temperature of the background black hole,are discussed.It is observed that the particular form of the metric leads to quasinormal frequencies whose real parts are numerically insignificant.The black hole metric is found to be stable against small scalar perturbations.

Key words:quasinormal modes,Lovelock theory,Horowitz-Hubeny method,matrix method

1 Introduction

Quasinormal mode,in general,is defined as an eigenmode of a dissipative system.A familiar example is the ringing noise of a wine glass when struck lightly on the side by a hard object.In the context of general relativity,small perturbations of a black hole metric may also lead to quasinormal modes.[1?3]Owing to the recent development of the holographic principal regarding the anti-de Sitter/conformal field theory(AdS/CFT)correspondence,the latter has been recognized as an essential tool for exploring the properties of a strongly coupled system.[4]In particular,one may be used to extract important physical quantities,such as the transport coefficients of the dual system,namely,viscosity,conductivity,and diffusion constants.The first detection of gravitational wave[5]has further pushed the frontier of the study into a new era related to precise measurements.

The study of black hole quasinormal mode was initiated by investigating the perturbations of the metric itself,[6?9]Subsequently,it is extened to the perturbations of scalar,[10?12]electromagtic tensor,[13?15]as well as Dirac spinor[16?20]residing outside the black hole horizon. The calculations have been carried out for asymmpototically flat,[21?24]AdS,and de Sitter(dS)spacetimes.[25?30]Moreover,modified gravity,such as Gauss-Bonnet and Dilaton theories,[31?36]squashed Kaluza-Klein black hole,[37?39]Lifshitz black brane[40]have also been extensively studied.

Besides analytic solutions for quasinormal frequencies,[41?43]it is often necessary to resort to numerical techniques.[44]Mathematically,the analysis of the quasinormal mode involves the solution of non-Hermitian eigenvalue problems in terms of coupled linear differential equations with the associated boundary conditions.Numerical methods have proposed.To name a few,these include the WKB method,[45?47]continued fraction method,[48?49]Poshl-Teller potential approximation,[50]Horowitz and Hubeny(HH)method for AdS black hole,[25]and finite difference method for the study of temporal evolution of the small perturbations.[51?52]Recently,some of us have proposed a matrix method[53?54]where the spatial coordinate is discretized so that the differential equation,as well as its boundary conditions,are transformed into a homogeneous matrix equation.A vital feature of the method is that the eigenfunction is expanded in the vicinity of all grid points,and therefore the precision of the algorithm is improved.[55]

As mentioned,the usefulness of the AdS/CFT correspondence lies in the relationship between the classical gravity system in the bulk and the strongly interacting gauge field theory on its low dimensional boundary.In this regard,the study of the properties of gravity in asymptotically AdS spacetimes has aroused considerable attention,with many applications such as those in holographic superconductors.[56?59]Recently,Gaete and Hassa?ne obtained a planar AdS black hole solution for a particular class of Lovelock gravity.[60]The theory concerns a nonminimally self-interacting scalar field,where the specific form of the interaction is determined by the spacetime dimensiond as well as a model parameter k.The latter results from the requirement for the theory to have a unique AdS vacuum.The Lovelock gravity with the presence of the scalar field is explored,and the authors found two classes of black hole solutions with planar event horizon topology.In particular,the theory is shown to restore to its general relativity counterpart when k=1,namely,the AdS vacuum with vanishing scalar field.Subsequently,the thermodynamics of the black hole solution[61]has been investigated.The background metric has also been employed to study the p-wave holographic superconductor in the dual space.[62]Many intriguing features related to the specify black hole metric have thus been discovered.It is therefore also interesting to investigate the stability of the metric in question regarding quasinormal modes.

In the present work,we study the scalar quasinormal modes of the planar black hole metric for a particular Lovelock theory.The paper is organized as follows.In the following section,we derive the master equation for scalar perturbations.Sec.3 presents the numerical results on the quasinormal frequencies by using the HH method and the matrix method.The temporal evolution of the perturbations is studied in Sec.4.The concluding remarks are given in the last section.

2 The Master Equation for Scalar Perturbations

In Ref.[60],two classes of planar AdS black hole solutions were obtained.It is further shown that these two classes of solutions are related to each other through a Kaluza-Klein oxidation.Therefore,in what follows,we will only consider the first family of the solutions.The black hole metric for d≥5 dimensional spacetime reads

where the integer k is related to the nonminimal coupling of the scalar field.The latter demands k≥2,as the scalar field vanishes for k=1.

The temperature of the black hole is given by

where rh=Mk/(d?2)is the radius of the black hole horizon.

By using coordinates transformation v=t+x and dr?=dr/f(r),we can rewrite Eq.(1)as

To discuss the stability of the above metric against perturbation of a massless scalar field Ψ,one writes down the Klein Gordon equation

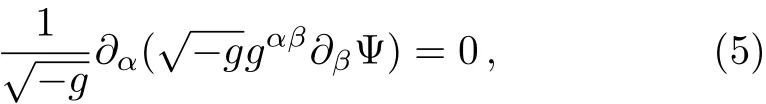
which can be rewritten explicitly in terms of individual components as

where ?randare shorthands for?/?r and ?2/?r2respectively.We make use of the method of separation of variables by assuming

subsequently the radial part of the equation is found to be

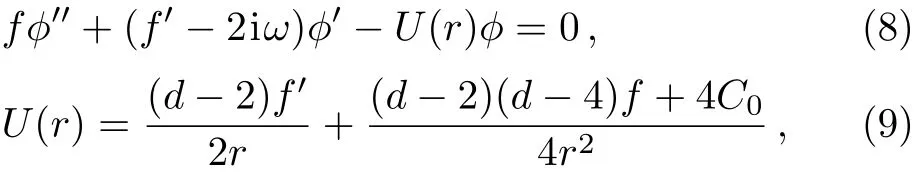
where C0is a constant and it is chosen to be 0 in in the following disscusions.

Following Ref.[53],we first introduce the variable z=(rh/r)1/2to replace the radial coordinate r,with the range z∈[0,1]corresponding to r∈[rh,∞].Then one defines σ(z)=(z ? 1)?(z)with the boundary condition σ(0)= σ(1)=0,and express the following equation of σ in matrix form

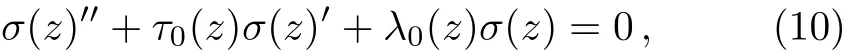
with

The obtained quasinormal frequencies will be presented in the next section in Table 1,Figs.1 and 2.

To employ the HH method,[25]we make use of the coordinate transformation x=1/r,and denote x+=1/rh.It is straightforward to show that Eq.(8)can be rewritten as

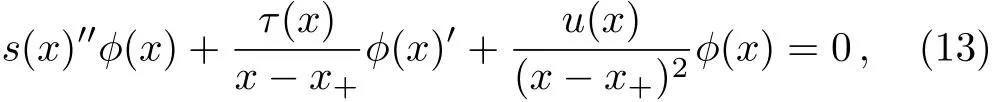
where

By expanding s(x),τ(x),and u(x)as follows

one deduces the recurrence relation

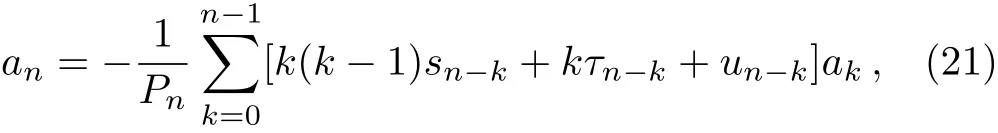
where Pn=n(n?1)s0+nτ0.By considering the boundary condition,as U(r)divergence at in finity,we require ?(x)→0 as r→∞(x→0),we set a0=1,thus one has

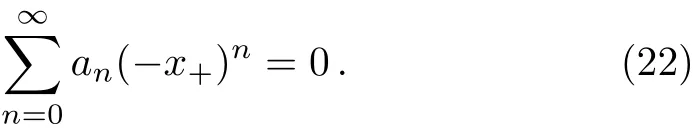
The numerical results of ω by solving Eq.(13)is presented in the following section in Table 1.

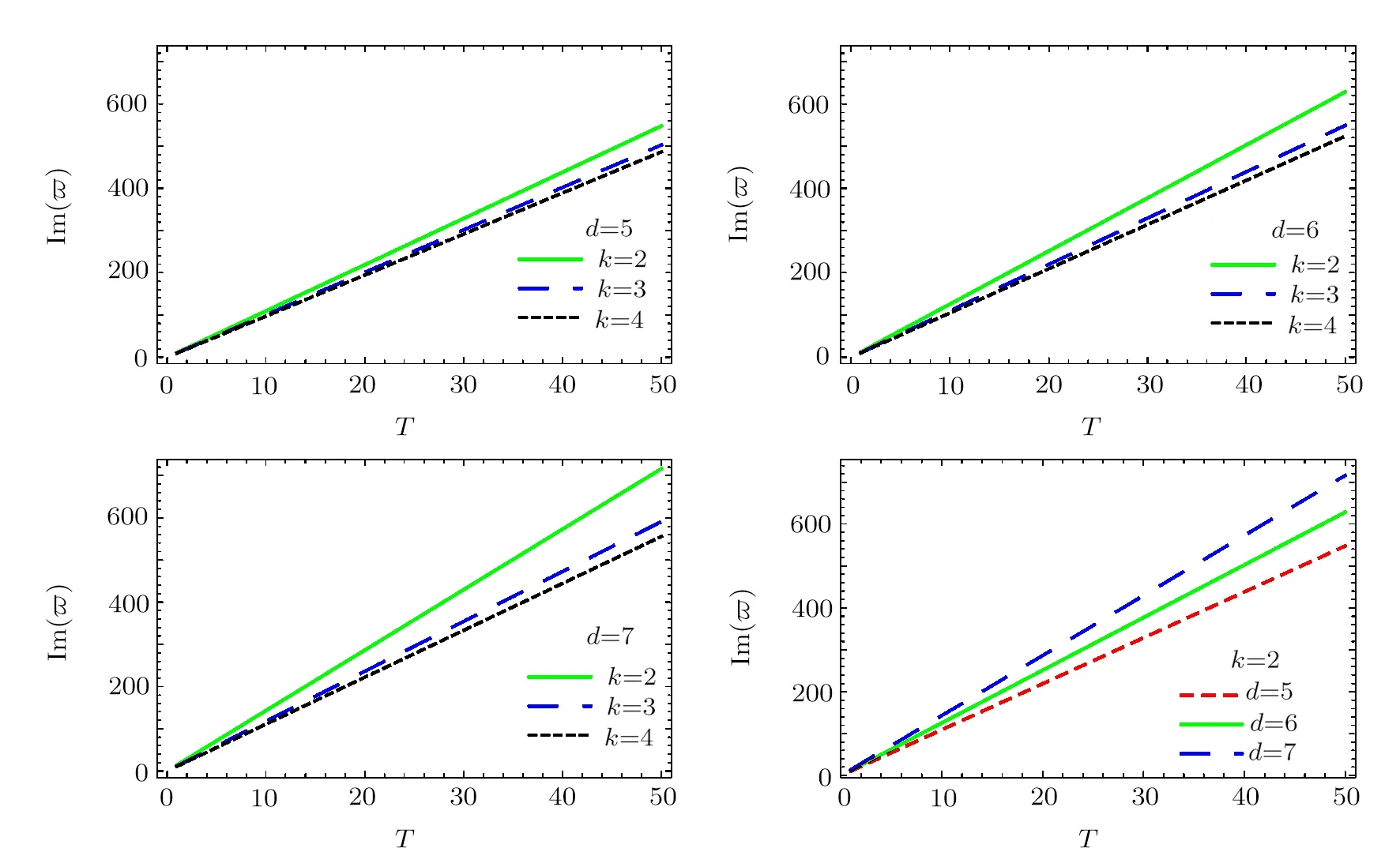
Fig.1 (Color online)The calculated imaginary part of the quasinormal mode frequency as a function of the temperature for d=5,6,7 dimensional planar AdS black holes.The calculations are done by using different model parameters k=2,3,4.

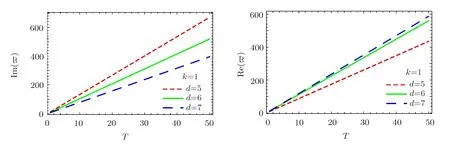
Fig.2(Color online)The calculated imaginary as well as real parts of the quasinormal frequencies as a function of the temperature for different model parameter k=1.The calculations are carried out for black holes with dimensions d=5,6,7.

3 Quasinormal Frequencies

In this section,we present the numerical results of the quasinormal frequencies obtained by using the methods described in the previous section.In Table 1,we show the evaluated quasinormal frequencies for different values of model parameter k.In particular,the case k=1 corresponds to that of the AdS vacuum in general relativity without the presence of the scalar hair and therefore can be compared to the known numerical values.[25]We have also carried out the calculations by using different radii of black hole horizon.It is found that the real part of the quasinormal frequency numerically vanishes when k>=2,different from the case when k=1.Therefore,one concludes that this characteristic is closed related to the existence of nonminimally coupled scalar hair for the present version of Lovelock gravity.Also,for a given value of rh,the imaginary part of the quasinormal frequency decreases as k increases.For a given k,the imaginary part of the quasinormal frequency is mostly proportional to the radius of the black hole horizon.All the calculations are carried out by both the HH method and the matrix method.As shown in Table 1,both methods give consistent results with a precision of five significant figures in most cases.

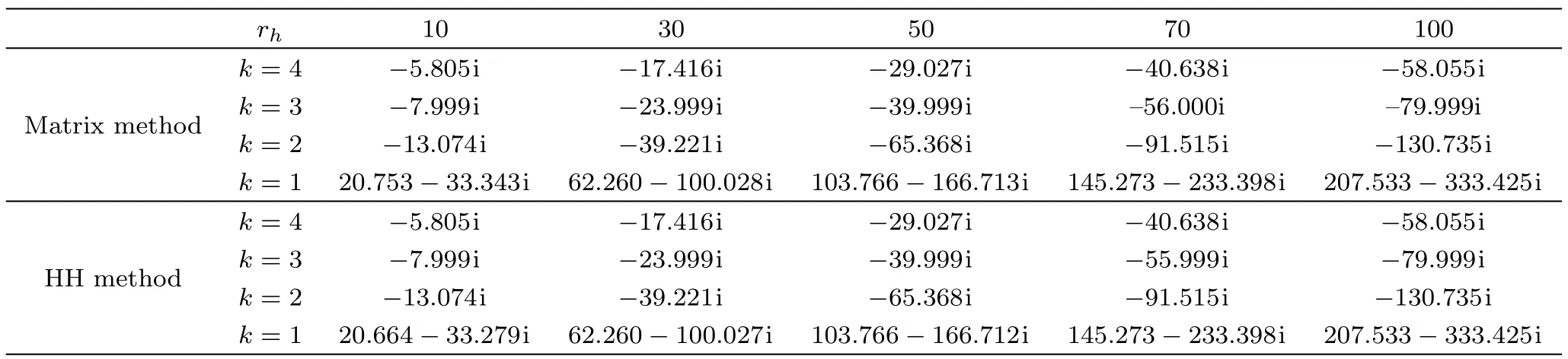
Table 1 The calculated quasinormal mode frequencies for d=5 dimensional planar AdS black hole and the corresponding limit case of AdS vacuum obtained by taking k=1.

In order to study the properties of the quasinormal frequencies,we present in Figs.1 and 2 the calculated imaginary and real parts of the frequencies.It is found that both the imaginary and real parts of the frequency are mostly linear as a function of the temperature of the black hole,similar to those obtained previously.The left panel of Fig.1 illustrates that imaginary part of the frequency decreases with increasing k.Moreover,the right panel of Fig.1 shows that for given k=2 the slope increases with the spacetime dimension.In Fig.2,we observe that in the case of AdS vacuum corresponding to k=1,in contrast,the imaginary part of the quasinormal frequency decreases as the dimension increases,which is similar to the case of Schwarzschild AdS black hole.[25]These results show that the presence of nonminimal scalar hair indeed modifies the properties of the quasinormal mode.

We further assume

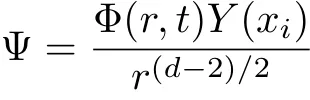
and introduce the tortoise coordinate dr?=dr/f(r).Then the eqution governing the temporal evolution reads

where V(r)=f(r)U(r).

The above equation can be solved numerically by employing the finite difference method.By dividing the spatial and temporal coordiantes into small grids,namely,t=t0+i?t and r?=r?0+j?r?,Eq.(24)can be discretized.One finds

4 Temporal Evolution of Small Perturbations

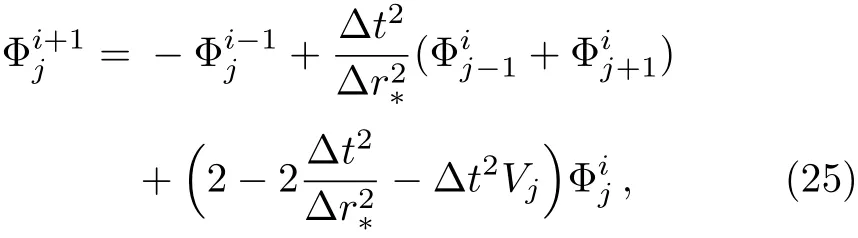
Now we are in a position to study the temporal evolution of the perturbations of a massless scalar field.By using the specific form of the metric,Eq.(1),the master field equation Eq.(5)can be expressed as

which we solve by using the following initial conditions

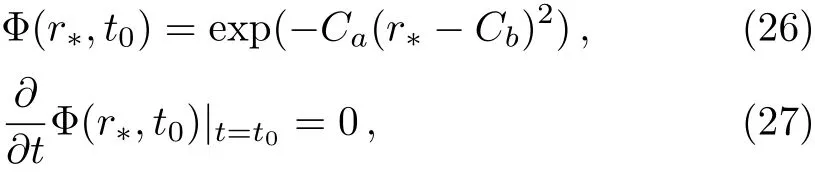
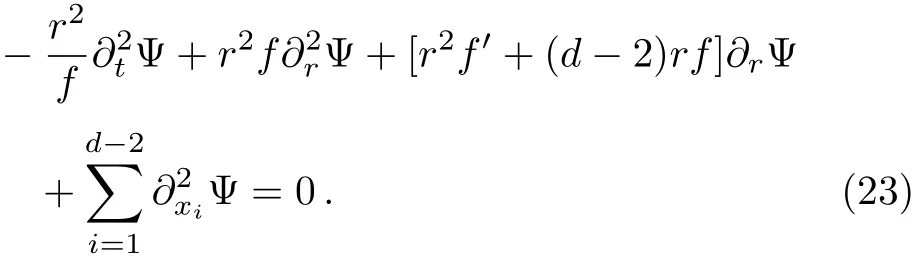
together with the Dirichlet conditions at anti-de Sitter boundary is Φ(r?,t0)|r?=0=0.Also,the Von Neumann stability is guaranteed by requiring

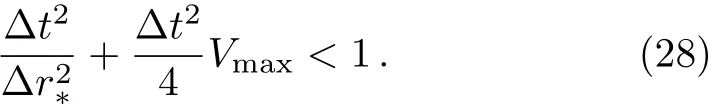
Fig.3 The temporal evolutions of the perturbations of a massless scalar field for different model parameters.

From Fig.3,it is found when k≥2,the decay of the perturbation increases with decreasing k,the oscillation is heavily quenched shortly after the initial phase.This is consistent with what was obtained in the preceding section,particularly concerning the results that the real part of the quasinormal frequency is numerically vanishing.For k=1,the decay is even faster than any other case where k≥2,temporal oscillations are also observed.Comparing the temporal evolution of perturbations for spacetimes with different dimensions,as shown in the right panel of Fig.3,one finds that the decay is more rapid as d increases.This is also in agreement with the findings in Sec.3.

5 Concluding Remarks

The proposed AdS/CFT correspondence has signi ficantly promoted many applications in various areas.In this context,the background black hole metric corresponds,in the dual system,a system in near thermodynamic equilibrium with its temperature related to the surface gravity of the black hole.As the quasinormal modes are closely associated with the AdS/CFT correspondence,its calculations have become increasingly important in particle physics.In this work,we numerically studied the quasinormal modes of the planar AdS black hole of a particular Lovelock theory.The calculations of quasinormal frequencies are carried out by using both the HH method and matrix methods.Temporal evolution of scalar perturbations is also studied by using the finite difference method.Both methods are shown to lead to consistent results.It is found that the presence of the nonminimally couple scalar hair non-trivially modifies the properties of the quasinormal frequencies.The real part of the quasinormal frequency is found to be numerically insignificant,and as a result,during the temporal evolution of the scalar perturbation,the oscillation is not observed after the initial phase.This feature is qualitatively different from that of AdS vacuum,which is restored in the present model by taking k=1.Besides,the dimension dependence of the decay rate also shows different characteristic for k≥2 cases in comparison to that with k=1.Our present study finds that the black hole metric in question is stable against scalar perturbations.