Guang-Han Peng(彭光含), Shu-Hong Yang(陽樹洪), and Hong-Zhuan Zhao(趙紅專)

1College of Physics and Electronics,Hunan University of Arts and Science,Changde 415000,China

2College of Physical Science and Technology,Guangxi Normal University,Guilin 541004,China

3School of Computer Science and Communication Engineering,Guangxi University of Science and Technology,Liuzhou 545006,China

4College of Architecture and Transportation Engineering,Guilin University of Electronic Technology,Guilin 541004,China

AbstractA feedback control model of lattice hydrodynamic model is proposed by taking the information of the historic optimal velocity into account for the traffic system.The modern control theory is applied for the linear stability condition with feedback control signal.The result shows that the stability of traffic flow is closely related to the information of the historic optimal velocity.Furthermore,numerical simulations conform that the new feedback control did increase the stability of traffic flow efficiently,which is in accord with theoretical analysis.

Key words:traffic flow,lattice hydrodynamic model,control method,traffic jam

1 Introduction

Traffic jams have been more and more attracted people’s attention.To solve the traffic jams,a considerable number of traffic models,such as the car-following models,the cellular automation models,the lattice hydrodynamic models,and coupled map models etc.,have been put forward.[1?22]These models of traffic flow can reproduce some complex phenomena of traffic flow.Furthermore,some scholars brought forward control method to improve traffic congestion. Firstly,a decentralized delayed-feedback control was introduced into the coupledmap(CM)car-following model proposed by Konishi,Kokame,and Hirata(called for KKH model).[23]Subsequently,a simple feedback control involving relative velocity was considered into CM model to suppress the traffic congestion.[24]Following this,a feedback control concerning multiple relative velocities was inserted into CM model.[25]Moreover,some other control patterns[26?29]have been drawn into car-following model to restrain traffic jam.In view of different perspectives,Ge et al.[30]applied the control theory into lattice hydrodynamic model to investigate the traffic jam.Hereafter,Redhu et al.[31]testified that the delayed-feedback control of traffic flux could stabilize the traffic flow in lattice hydrodynamic model.Also Li et al.[32]proposed a new control method by considering the density change rate difference in lattice hydrodynamic model.Zhu et al.[33]put forward the control signal with the consideration of the variation rate of the optimal velocity in lattice hydrodynamic model.However,up to present,the effect of the historic optimal velocity difference has not been debated in the lattice hydrodynamic model.In real,the historic optimal velocity usually exerts an important in fluence on traffic flow.Therefore,a new feedback control pattern including the historic optimal velocity will be designed to increase the stability of traffic flow for the lattice hydrodynamic model.

The outline will be arranged as follows:In Sec.2,a new feedback control pattern will be proposed with the consideration of the historic optimal velocity difference.In Sec.3,we apply the control theory to get the linear stability of the extended model.In Sec.4,numerical simulations are carried out for the lattice hydrodynamic model with control signal.Finally,the conclusions are derived in Sec.5.

2 Lattice Model with New Control

The original lattice hydrodynamic model was put forward by Nagatani[18?19]as follows:

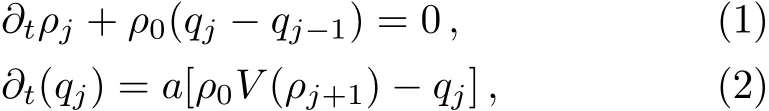
where ρ0, ρj,and qjexpress the average density,the local density,and local flux on site j,respectively.a=1/τ means the sensitivity of a driver.And the optimal velocity function V(ρ)is chosen as below:

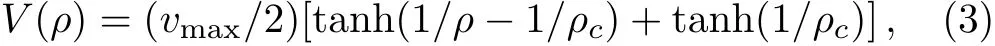
where ρcrepresents the safety density.We suppose that the density and flux of the traffic flow system have the steady-state uniform flow solution with the form as below:

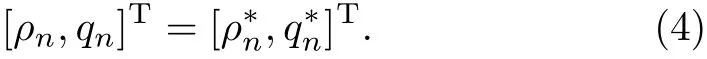
In real traffic flow,the historic information often plays an important role on drivers’behaviors.And the optimal velocity represents the desired state of traffic flow.Incorporating these two aspects,the state of traffic flow can be adjusted according to the difference between the current optimal velocity and historic optimal velocity on site j+1 when traffic congestion aggravates.Therefore,based on this reason,we adopt a new control signal Ajas below:

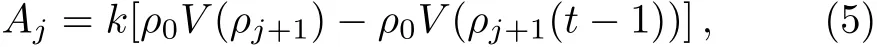
where k shows the feedback gain derived from site j+1.It is clear that the control signal is resulted from the difference between the current optimal velocity and historic optimal velocity on site j+1.That is to say,drivers’behavior will be adjusted by historic information of optimal flow on site j+1.Therefore,we deduce a new lattice hydrodynamic model with control signal Ajas follows:

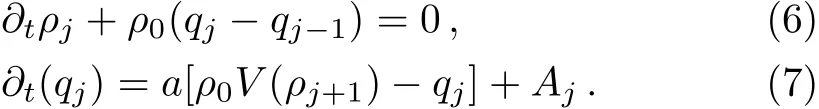
Then,Eqs.(6)and(7)can be rewritten as follows:

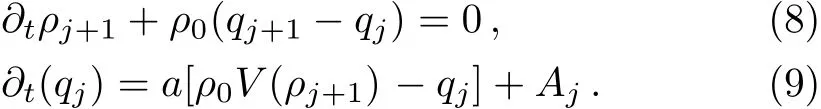
3 Linear Stability Analysis

In this section,we utilize control theory to implement the linear stability analysis.The steady-state uniform flow solution is supposed as[ρn,qn]T=[ρ?,q?].By linearizing the system of Eqs.(8)and(9)around the steady state,we derive whereand Λ2=By taking Laplace transform for Eqs.(10)and(11),one obtains

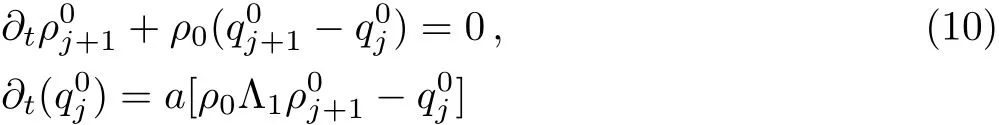
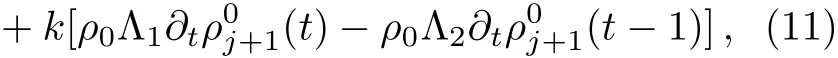
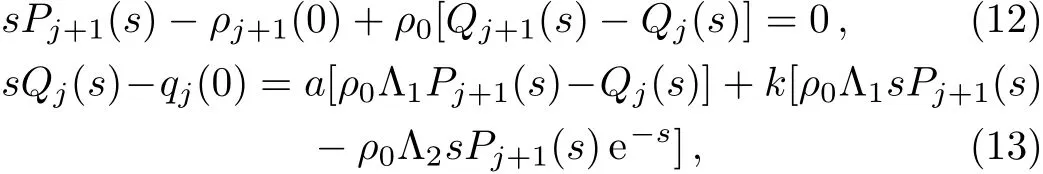
where Pj+1(s)=L(ρj+1),Qj(s)=L(qj),Qj+1(s)=L(qj+1),L represents the Laplace transform.By incorporating Eqs.(12)and(13),we win the Laplace transform equation of traffic flux as below:

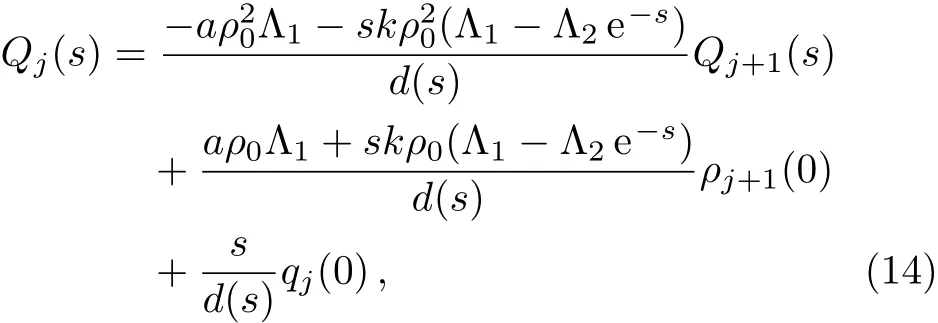
where d(s)is the characteristic polynomial:

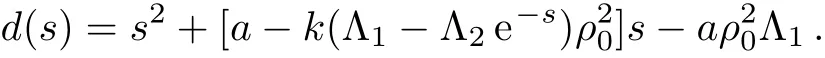
And the transfer function G(s)is derived by

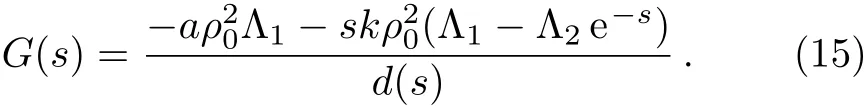
By applying Taylor’s formula and linearizing Eq.(15),we can rewrite it as below:

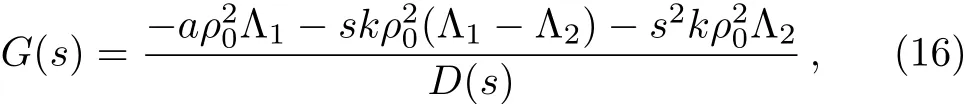
where

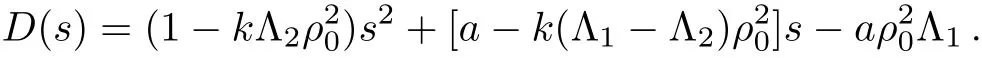
According to Definition 1,[23]thetraffic congestion never appears when the characteristic polynomial D(s)is stable and the transfer function ∥G(s)∥∞=supw∈[0,∞)|G(jw)| ≤ 1. From the Hurwitz stability criterion,[29]if[a ? k(Λ1? Λ2)>0 and>0 are satisfied the polynomial D(s)is stable.According to∥G(s)∥∞=supw∈[0,∞)|G(jw)|≤ 1,the result can be described by

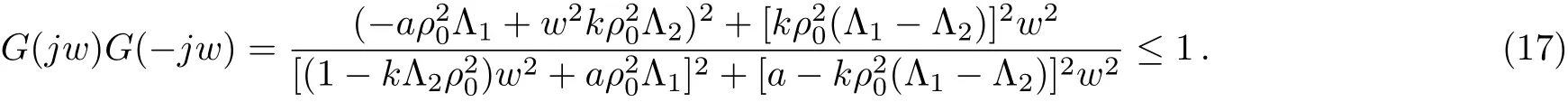
Obviously,G(0)=1.In the light of|G(jw)|≤1,w ∈[0,∞),one receives the sufficient condition as below:

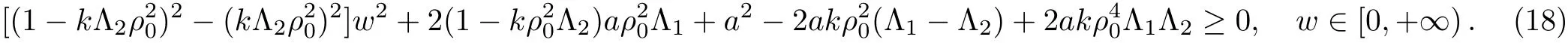
Therefore,we acquire the sufficient condition corresponding to Eq.(18)as below:

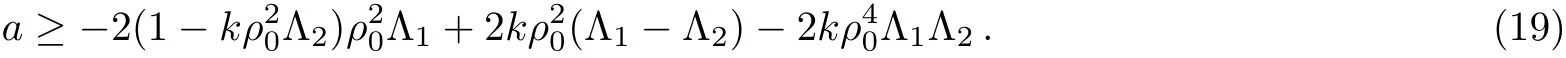
It indicates that the traffic disturbance is not amplified when the above stability conditions are satisfied,which means that the traffic jams are suppressed.It is clear that the sufficient condition is bound up with the feedback gain.Thus we can design the feedback gain for the lattice hydrodynamic model to restrain the traffic congestion on the basis of the sufficient condition.

4 Numerical Simulation

Numerical simulation in this section will be considered to investigate the effect of the new control method for the lattice hydrodynamic model.Analogously,the parameters will be same as that in Ref.[30]:N=140,ρ0=0.25 and vmax=2.And the lattice density of the number 50 to 55 is 0.5 and the number 56 to 60 is 0.2.The following results are mainly the numerical simulation for the temporal density and flux of the first,25th,55th,and 80th lattice.

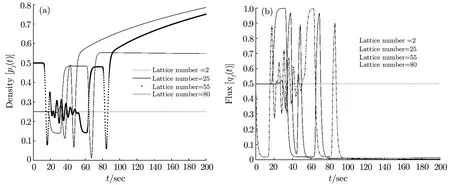
Fig.1 The diagrams of density and flux without control signals when a=0.7 and k=0.

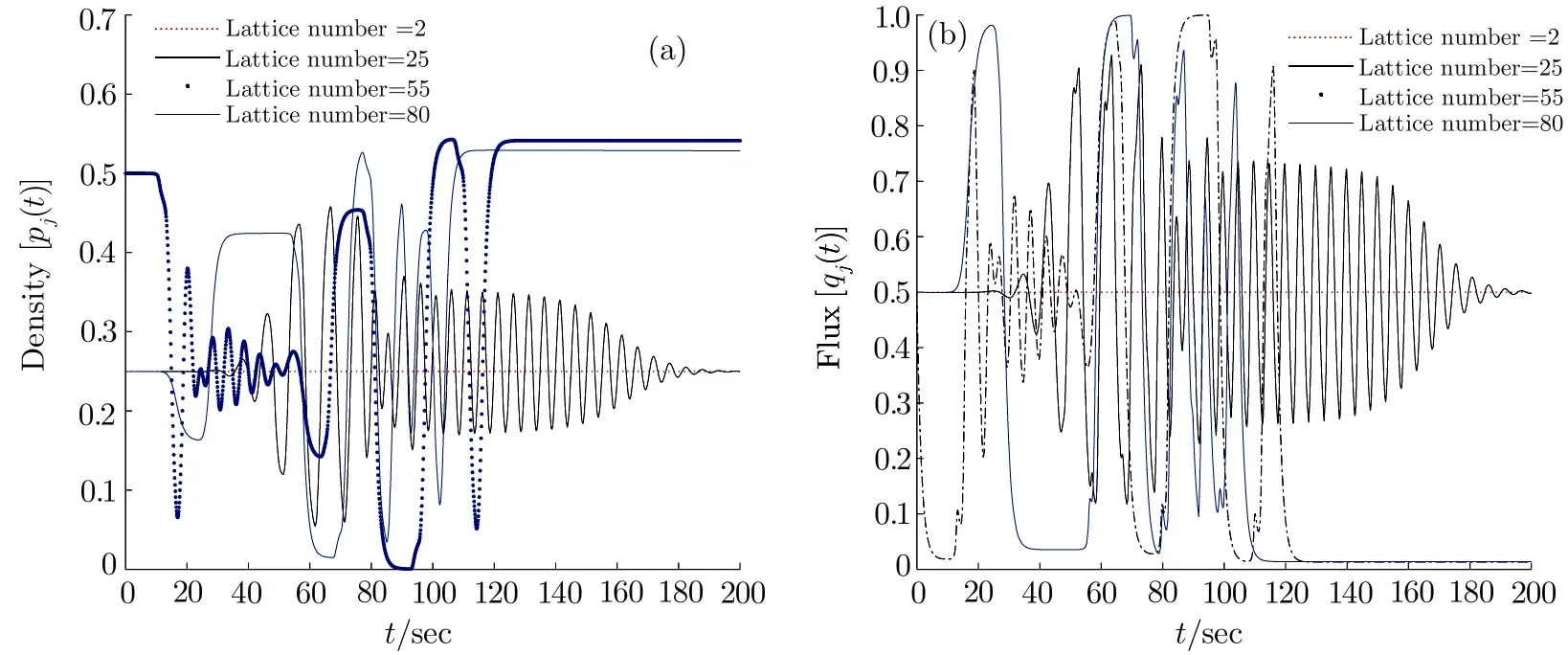
Fig.2 The diagrams of density and flux without control signals when a=0.7 and k=0.5.

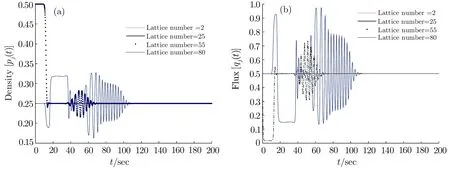
Fig.3 The diagrams of density and flux without control signals when a=2.6 and k=0.

Figures 1 and 2 show the diagrams of density and flux without and with control signals in instability condition,where a=0.7.Figure 1 is same as that in Ref.[30].From Figs.1 and 2,there appears the traffic congestion under the stable condition.It is shown the distinction between Figs.1 and 2 that traffic congestion becomes smoother with the new control signal.Figure 3 reveals the diagrams of density and flux without control signal under the stability condition.And Figs.4–6 emerge the diagrams of density and flux with control signals under the stability condition for the feedback gain k=0.3,0.5,and 0.8,respectively.where a=2.6.It is found that the traffic flow evolves gradually into the steady state with the increase of the feedback gain k from Figs.3 to 6.It is obvious that the new control signal can alleviate traffic congestion and relieve the oscillating effectively via numerical simulation.In a conclusion,the feedback control signals of the historic optimal velocity difference improve the steady of traffic flow.

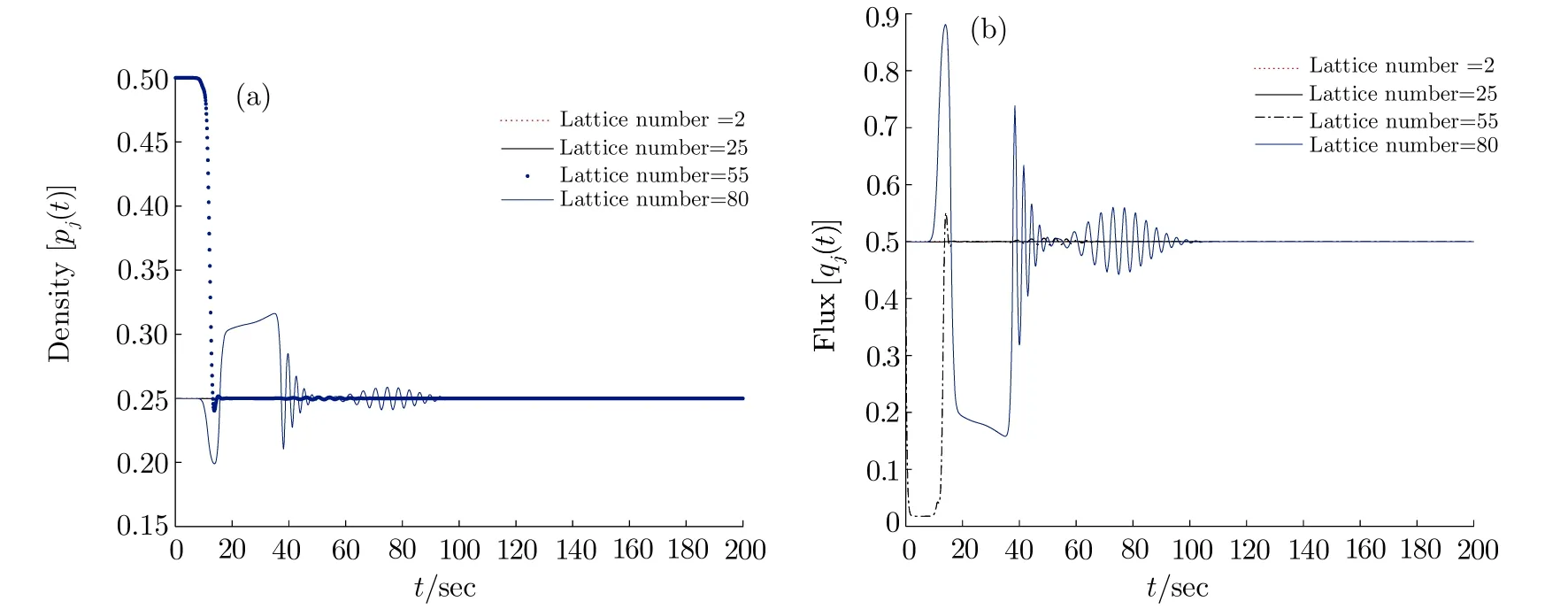
Fig.5 The diagrams of density and flux without control signals when a=2.6 and k=0.5.

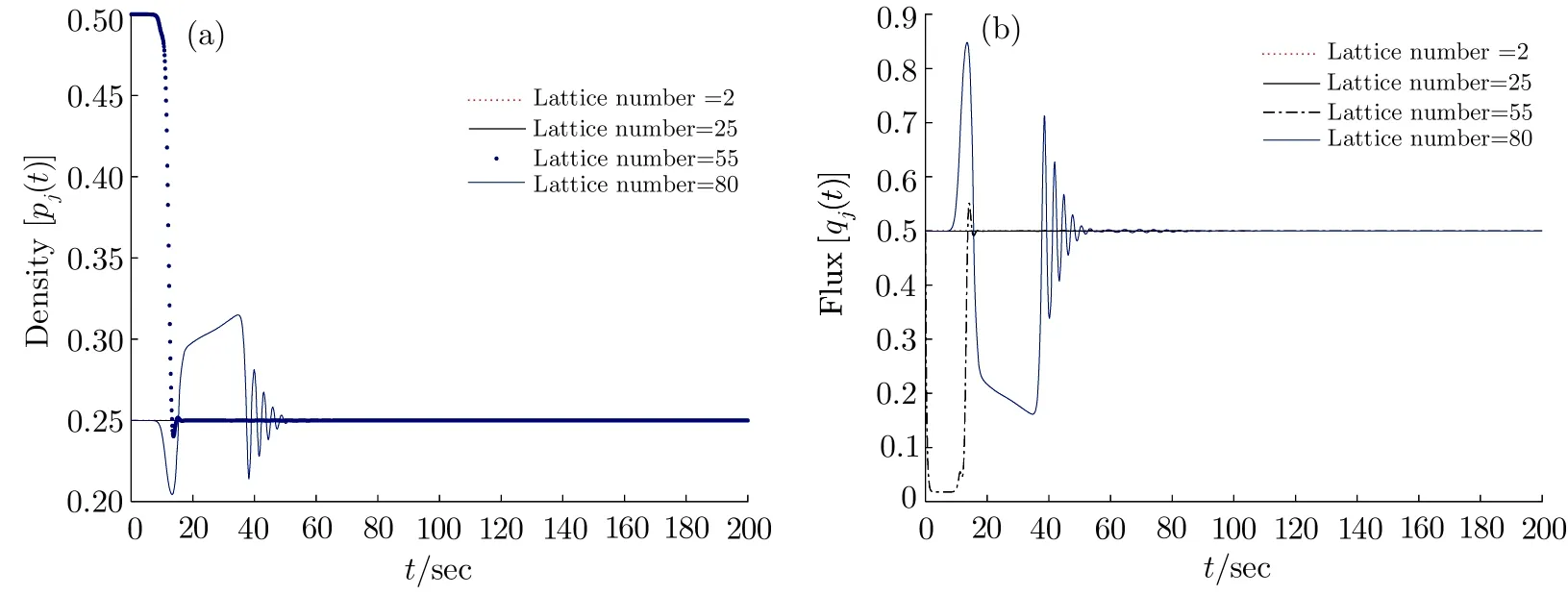
Fig.6 The diagrams of density and flux without control signals when a=2.6 and k=0.8.

5 Conclusion

In this paper,we apply the control theory to improve traffic model.A new control strategy is adopted with the consideration of the historic optimal velocity difference.The sufficient condition of stability is obtained and the feedback gain can be designed according to the control method.Numerical simulations provide the evidence that the new feedback control signal can restrain the traffic congestion,which implies that the historic optimal velocity difference effect can improve the stability of traffic flow.Certainly,how to design relevant parameters is what we will study in the future.