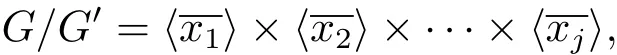薛海波,張 鈺,呂 恒

(1.重慶人文科技學(xué)院機(jī)電與信息工程學(xué)院,重慶合川 401524)

(2.西南大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,重慶 400715)

1 引言

設(shè)G為群,H是G的子群.則H在G中的正規(guī)閉包HG定義為G中包含H的最小正規(guī)子群.于是H是G的正規(guī)子群的充要條件就是|HG:H|=1.因此從某種意義上來說,|HG:H|可以反映出子群H 的正規(guī)性.|HG:H|越接近1,那么H的正規(guī)性越強(qiáng).眾所周知所有子群都是正規(guī)子群的群是Dedekind群.如果一個群G的任意非正規(guī)子群H的閉包滿足|HG:H|=p,其中p是一個素?cái)?shù),那么這類群就與Dedekind群越接近.文獻(xiàn)[1–3]分別對這類有限p-群或有限可解群進(jìn)行了詳細(xì)的研究,證明了這類群的換位子群的階存在一個上界.

一個群G的任意非正規(guī)子群H的閉包滿足|G:HG|=1或者素?cái)?shù)p,則可以看作是子群的正規(guī)性比較弱的情況.顯然所有單群就滿足這樣性質(zhì).除單群外,讓人感興趣的是滿足這類條件的冪零群與可解群.對于冪零群,Janko首先在文獻(xiàn)[4]中研究了有限p-群G,其任意非正規(guī)子群H的正規(guī)閉包HG滿足|G:HG|=p,得到了

定理1.1 對于一個非Dedekindian p-群G,如果G的任意非正規(guī)循環(huán)子群H,都有|G:HG|=p,那么G為下列群之一

(a)|G|=p3.

(b)G=ha,b|ap2=bp2=1,ab=a1+pi是唯一階為p4非交換亞循環(huán)群且exp(G)=p2.

(c)G是極大類2-群.

(d)G=hh,z|h4=z2n=1,n>2,zh=z?1+?2n?1,?=0,1i.

作為Janko研究工作的繼續(xù),本文將研究滿足下面性質(zhì)的有限可解群G:對任意的x∈G,若hxi不是G的正規(guī)子群,則都存在一個素?cái)?shù)p使得|G:為了敘述方便,下文稱滿足這個條件的群為MC-群.由引理2.2,若MC-群為冪零群時,則一定為p-群.鑒于Janko已經(jīng)完成了這類群的分類,本文將研究可解但非冪零的MC-群,主要得到如下的結(jié)果.

定理1.2 設(shè)群G是有限可解群.如果G是非冪零的MC-群,那么G/G0是階為p1m的循環(huán)群與階為p2n的循環(huán)群的直積,其中p1,p2分別是素?cái)?shù),m≥1,n=0或1.更進(jìn)一步,

(1)若n=0,則G=A o hyi,其中yp1m=1,A=G0是Hall p10-群,且有下列(1.1)–(1.3) 結(jié)論成立.

(1.1)若m=1且G0交換,則G0是初等交換p3-群;或G0=其中o(a1)=p3n,o(a2)=p3,n≥2;或G0是所有子群均正規(guī)于G的p10-群.

(1.2)若m=1且G0非交換,則G0是特殊p3-群,即G00=Z(G).故G0的冪零類為2.特別地,若p3≥3,則exp(G0)=p3;若p3=2,則exp(G0)≤22.

(1.3)若m≥2,則G0是所有子群均正規(guī)于G的p10-群.

(2)若n=1,則G/G0是兩個不同素?cái)?shù)方冪階的循環(huán)群的直積,|G/G0|=p1mp2.此時G0中每個子群均正規(guī)于G,且有下列(2.1)–(2.3)結(jié)論成立.

(2.1)若p1=p2,則G=Gp1n Gp10,其中Gp1為G的Sylow p1-子群,Gp10為G 的Hall p01-子群,且Gp106 G0,而且Gp1=hx1i×hx2i,o(x1)=p1m,o(x2)=p1或Gp1同構(gòu)于定理1.1 Janko所分類的亞循環(huán)群.

(2.2)若m=1且p16=p2,則G=()n G0,其中o(x1)=p1,o(x2)=p2.

(2.3)若m≥2且p16=p2,則G=(Gp1n G0)×其中Gp1是p1m階循環(huán)群,G0是一個p01-子群,o(x2)=p2.

2 主要結(jié)論及證明

引理2.1[6]設(shè)π0-群H 作用在交換π-群G上,則G=CG(H)×[G,H].

引理2.2設(shè)G是MC-群,則G是冪零群當(dāng)且僅當(dāng)G是p-群.

證 僅需證明必要性.因?yàn)槿篏 是冪零群,所以G=Sp1×Sp2×···×Spk,其中Spi∈Sylpi(G),i=1,···,k是Slyow pi-子群.不妨設(shè)x∈Sp1且不是G 的正規(guī)子群.顯然hxiG

引理2.3設(shè)G是交換p-群.若a∈GGp且a是aGp中階最小的元,則存在子群G0使得G=hai×G0,其中Gp=hgp|g∈Gi.

引理2.4設(shè)有限群G是MC-群.若|G|=pmqn,p>q都是素?cái)?shù),且G/G0～=Cp×Cq,則|G|=p2q或者|G|=pq.

證 顯然G0中所有子群都是正規(guī)子群.令G0=M×N,其中M,N分別是G0的Sylow p-子群和Sylow q-子群.考慮商群ˉG=G/M,易得的Sylow q-子群與G的Sylow q-子群同構(gòu)且G/G0.因此不妨假設(shè)G的Sylow p-子群是p階循環(huán)群.此時G的Sylow q-子群是正規(guī)子群.

下面證明G的Sylow q-子群Q是階小于或者等于q2的初等交換群.

先假設(shè)Q是交換群.證明Q是階小于或者等于q2的初等交換群.由引理2.1可知Q=CQ(hxi)×,Q],且[hxi,Q]=G0.因?yàn)镚0是Q的真子群,所以CQ是q階循環(huán)群.此時顯然G0∩CQ(hxi)=1.若G0=1,則Q是q階循環(huán)群,結(jié)論顯然成立.假設(shè)|G0|>1.任意取q階元b∈G0,則hbi E G.于是hai×hbi E G.由于[a,x]=1,[b,x]6=1,故(ab)x=abk,其中(k,q)=1.此時易得habi不是群G的正規(guī)子群.從而說明habiG=Q是階為q2的初等交換子群.

下面證明Q一定是交換群.假設(shè)Q是非交換q-群.因?yàn)镚0的所有子群均正規(guī)于G,所以對任意的g∈G0都有hgiEG.又由G/CG(hgi)～=Aut(hgi),即G/CG(hgi)是交換群.于是G0≤CG(hgi)且g∈Z(G0),故G0是交換群.設(shè)z∈QG0.若hzi是G的正規(guī)子群,類似可得G0≤CG(hzi).而Q=hz,G0i,于是得Q是交換群,與假設(shè)相矛盾.故hzi不是G的正規(guī)子群.因此有Q=hziG.考慮商群=G/Q0.顯然=也是MC-群.由前面Q是交換的情況的討論可知=q2,故Q=

若q≥3,由于|Q:G0|=q且G0中所有子群均正規(guī)于G,則G0是交換群且存在x0∈QG0使得Q=G0·hx0i.任取g∈G0都有hgiEQ,[xq0,g]=1,因此[x0,g]∈Z(Q)是q階元.故Q0≤Z(Q).于是cl(Q)=2,從而得到Q是正則q-群.

顯然hzqi≤G0是正規(guī)子群.因此hzi∩hzxi=hzqi.假設(shè)o(z)≥q2,利用Q的正則性,存在q階元z1∈Q使得Q=hz,zxi=hz,z1i.此時?1(Q)=hg|gq=1,g∈Qi是Q的方次數(shù)為q的真子群.于是得到?1(Q)中所有子群正規(guī),即hz1i≤Z(Q).從而得到Q是交換群,矛盾.

下設(shè)o(z)=q,則exp(Q)=q且|Q|=q3.因此G0≤Q為q2階的初等交換q-群.又因?yàn)镼是非交換群,所以存在z3∈G0使得hz3i不是Q的正規(guī)子群.這與G0的每個子群均正規(guī)于G矛盾.故Q是交換群.

若q=2,由于|Q/Q0|=4以及文獻(xiàn)[7,命題1.6]可知,Q是極大類2-群.當(dāng)|Q|=23時, 則 Q ～=D8或 Q ～=Q8. 若 Q ～=D8, 則 Aut(Q) ～=Aut(D8) ～=D8. 由于 p 6=q, 因此[hxi,Q]=1,即表明G 是冪零群.若 Q ～=Q8,由 Aut(Q)～=Aut(Q8)～=S4可知 p=3,此時可得G0=Q,矛盾.

當(dāng)|Q|≥24時,則存在子群N ≤G0≤Q使得Q/N是階為23的非交換2-群,此時Q/N ～=D8, 從而=G/N=×,其中=xN,=Q/N,這與相矛盾.

綜上所述,Q是交換群.即Q是階小于或者等于q2的初等交換q-群.類似考慮商群=G/N,易得的Sylow p-子群與G的Sylow p-子群同構(gòu)且.因此不妨假設(shè)G的Sylow p-子群是p階循環(huán)群的情況下可得G的Sylow p-子群是階小于或者等于p2的初等交換p-群.

最后證明|Q|=q.假設(shè)|Q|=q2.同樣在商群=G/N中,則的Sylow q-子群階為q2的正規(guī)初等交換q-子群.而|Aut()|=(q2?1)(q2?q)且p>q.由6=1可得p=3,q=2.易得此時即矛盾.故|Q|=q.

定理1.2的證明 由于G/G0是交換群,故存在x1,x2,···,xr∈G使得

其中j是使得直積個數(shù)最多的整數(shù)值.

若j≥3,則對任意x∈G0都有hxi E G.令Hi=hxi,G0i,同樣可得hxii E G.而G=hx1,x2,···,xj,G0i,進(jìn)而得到G是Dedekind群,與G是MC-群相矛盾.因此j≤2,即|G/G0|=p1mp2n,其中p1,p2是素?cái)?shù),m≥1,n=0或1.

情形(1)n=0且G/G0是階為p1m的循環(huán)群,即|G/G0|=p1m.分以下三種情況討論.

(1.1)m=1且G0是交換群.

假設(shè)存在x∈G0使得hxi不是G的正規(guī)子群,則易得G0=hxiG且G0是交換p3-群,其中p3是素?cái)?shù).因?yàn)镚不是冪零群,所以素?cái)?shù)p36=p1.于是存在y∈G使得G=hyi n G0,其中o(y)=p1.又由 G0=hxiG可知x是G0中最高階元素,于是hxp3i E G,則h(xy)p3i∩hxi=hxp3i,故

其中o(x1)=p3,且EG.若o(x)=p3,則|G|≤p3p1且exp是初等交換 p3-群.

若o(x)=p3n>p3,則E G.令子群因?yàn)?/p>

所以H E G.故G0=,其中o(x)=p3n,o(x1)=p3.

假設(shè)G0中所有子群都正規(guī),僅需證明G0是群G的Hall p20-群.設(shè)N 是G0的Hall p20-子群,則G/N 是p2-群,且G/N–(G/N)0～=G/G0是循環(huán)群.故G/N 是循環(huán)群.因此G0=N是G的Hall p20-群.

(1.2)m=1且G0是非交換群.

假設(shè)對任意x∈G0均有hxi E G,則可知G/CG()是交換群.于是G06 CG(),從而得到G0是交換群,矛盾.因此一定存在x∈G0使得不是G的正規(guī)子群,故G0=G.因?yàn)镚是可解群,所以G00的所有子群均正規(guī)于G.于是對任意的a∈G00都有G/CG()是交換群,故G00是交換群且G00≤Z(G0).因此G0是冪零群且cl(G0)≤2.由于G不是冪零群,易得G0是群G的一個Sylowp3-群,進(jìn)而存在y∈G使得G=hyi n G0,其中o(y)=p1,|G0|=p3k,k≥1.

當(dāng)p3≥3時,因?yàn)閏l(G0)≤2,所以G0是正則p3-群.假設(shè)o(x)>p3.則由G0=hxiG可知,一定存在g∈G使得[x,xg]6=1.令H=因?yàn)閤p3∈Φ(G0),所以hxp3iEG.于是h(xg)p3i=hxp3i.故有正整數(shù)k使得

又因H正則,所以(x?kxg)p3=1,于是有H=hx,x?kxgi.記a=x?kxg,則haiG≤?1(G0)

當(dāng)p3=2時,假設(shè)o(x)=2t≥23.對任意g∈G令H=其中[x,xg]6=1.因?yàn)閏(H)≤2,所以H0=.又由x2∈Φ(G0),則hx2i E G,于是x2∈Z(G0).故由G0的冪零類是2可得[x,xg]2=[x2,xg]=1,因此H0是2階子群.且x2=(xg)2.由Hall-Petrescu恒等式(見文獻(xiàn)[7])可知

其中c2∈.令b=x?1xg,則H=hx,x?1xgi=.若hbi不是G 的正規(guī)子群,則G0=.因此對任意的z∈G0,有z=bl1(bg1)l2···(bgn)ln,其中g(shù)i∈G,li是整數(shù),1≤i≤n.又由Hall-Petrescu恒等式,對n歸納可知,o(z)≤4,故exp(G0)≤4,矛盾.因此hbi E G,所以類似可得G0≤CG(hbi),故H是交換群,與[x,xg]6=1相矛盾.因此o(x)≤22,exp(G0)≤22.

假設(shè)G00是Z(G0)的真子群.由文獻(xiàn)[6,定理2.2]存在正規(guī)子群N 使得G00≤N 且G0/G00=Z(G0)/G00×N/G00.由G0非交換,可得|N/G00|≥p32且N 是非交換p-群,又N是G0的真子群,因此N 的每個子群都正規(guī)于G.類似可得N中每個循環(huán)子群包含在Z(G0)中,于是N 是交換群,矛盾.故Z(G0)=G00,從而得到G0是特殊p3-群.

(1.3)m≥2.顯然G0的每一個子群均正規(guī)于G.此時斷言(|G0|,p1)=1.否則不妨設(shè)|G0|=p1nr,令G0=Q×R,其中|Q|=p1n,(|R|,p1)=1.記ˉG=G/R,則ˉG是p2-群且～=G/G0.而G/G0是循環(huán)群,于是ˉG/ˉG0是循環(huán)群.由此表明ˉG是循環(huán)群,故G/R是交換群.進(jìn)而有G06 R,與G0=Q×R相矛盾.所以存在y∈G使得G=hyi n G0,其中o(y)=p2m,m≥2,且G0是所有子群均正規(guī)于G的p20-群.

情形(2)G/G0是階為的循環(huán)群與階為p2的循環(huán)群.依然分以下三種情況討論.

(2.1)若p1=p2,則G=Gp1n Gp10,其中Hall p10-子群Gp106 G0.此時G0的每個子群均正規(guī)于G.若Sylow p1-子群Gp1的每個子群均正規(guī)于G,則G是Dedekind群,與題設(shè)條件相矛盾.若Gp1交換,則G/Gp10交換,于是G0=Gp10.從而存在x1,x2使得Gp1=其中o(x1)=p1m,o(x2)=p1.若m≥2,則hx2i E G,于是x2∈Z(G),從而有G=()n Gp10=(.若m=1.因?yàn)镚0中所有子群都正規(guī),所以不妨設(shè)G0是素?cái)?shù)階循環(huán)群.則|G:CG(G0)|=p1.因此也可以設(shè)x2∈Z(G).如果G0是不是素?cái)?shù)方冪循環(huán)群,那么存在正規(guī)子群N使得G0/N是素?cái)?shù)方冪循環(huán)群.在商群G/N中類似可得x2N∈Z(G/N).于是由hx2,Ni E G可得x2∈Z(G),從而得到G=(hx1i n Gp10)×hx2i.

若Gp1非交換,類似前面設(shè)Gp10是素?cái)?shù)階循環(huán)群,則易得G/CG(Gp10)是循環(huán)群,且CG(Gp10)=Gp10×S1EG,其中S1≤Gp1.顯然S1中所有子群都正規(guī)于G,又G/Gp10～=Gp1也是MC-群.此時Gp1同構(gòu)于定理1.1中Janko所分類的群.如果即Gp1不是亞循環(huán)群,那么由定理1.1可得Gp1只能是方次數(shù)為p1的且階為p31的非交換p1-群.于是S1～=Cp1×Cp1,即是階為p21的初等交換p1-群.又S1中所有子群正規(guī),故S1≤Z(G).從而得到Gp1是交換p1-群,矛盾.故Gp1是亞循環(huán)群.

(2.2)p16=p2且m=1.

因?yàn)镚0中所有子群均正規(guī)于G,所以G0是交換群.故G0=H×K,其中K是G0的Hall{p1,p2}0-子群.不妨設(shè)p1>p2.由引理2.4可得|G/K|=p12p2或p1p2,且當(dāng)|G/K|=p12p2時,由引理2.4的證明可得G的Sylow p1-子群是階為p12的初等交換子群.此時可得G0=K×Cp1.故可得G=n G0,其中o(x1)=p1,o(x2)=p2.

(2.3)p16=p2且m≥2.由于中每個子群均正規(guī)于G,則G,故 G=Gp1n Gp10. 又因?yàn)殡A循環(huán)群.所以Gp1是p1m階循環(huán)群.

令K 是群G的Hall{p1,p2}0-子群,則=Gp2×K 每一個子群正規(guī)于G,其中Gp2是G的Sylow p2-群.又設(shè)x2是G中階最小的元素使得x2G0是商群G/G0中的p2階元.顯然o(x2)=p2n.

下面證明n=1.顯然x2/∈(Gp2)p2.由引理2.3可知,存在子群G1使得Gp2=×G1,G1E G.

由上述定理1.1,可得下面推論.

推論2.5 如果有限可解群G是MC-群,那么G的導(dǎo)長至多是3.

顯然,定理1.2中(1.2)就存在導(dǎo)長是3的例子:G=Q8o C3,即四元數(shù)群Q8與3階循環(huán)群的半直積.