福建省龍海第一中學(xué)新校區(qū) 陳藝平 蘇藝偉

對于導(dǎo)數(shù)壓軸試題中的導(dǎo)函數(shù)零點(diǎn)不可求問題,經(jīng)常虛設(shè)零點(diǎn),整體代換,可以化繁為簡,化抽象為具體,順利實(shí)現(xiàn)轉(zhuǎn)化.本文以全國卷幾道導(dǎo)數(shù)壓軸試題進(jìn)行說明.

例1(2017年全國 II卷理科第21題)已知函數(shù)f(x)=ax2?ax?xlnx,且f(x)≥0.

(1)求a;

(2)證明:f(x)存在唯一的極大值點(diǎn)x0,且e?2＜f(x0)＜2?2.

解析(1)a=1,過程從略.

圖1

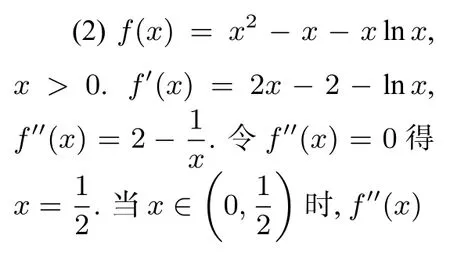
通過上述幾道全國卷高考試題的分析,不難發(fā)現(xiàn)全國卷高考試題偏愛此類導(dǎo)函數(shù)零點(diǎn)不可求問題.對于導(dǎo)函數(shù)零點(diǎn)不可求的問題,在虛設(shè)零點(diǎn),整體代換的過程中必須把握好兩個(gè)原則.原則一:在虛設(shè)零點(diǎn)的過程中,對隱零點(diǎn)的估值區(qū)間要盡量縮小.原則二:在整體代換的過程中,要把握好用什么樣的式子代替什么樣的式子(其依據(jù)是使得計(jì)算簡潔,解題過程流暢).如果忽略了這兩個(gè)原則,不僅會(huì)使得解題過程較為繁瑣,甚至?xí)贸鲥e(cuò)誤結(jié)果.