景書杰,王慧婷,牛海峰,陳 耀

(河南理工大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,河南焦作 454000)

1 引言

考慮如下無約束優(yōu)化問題

其中f(x)是Rn?→R上的連續(xù)可微函數(shù),用非線性共軛梯度法求解無約束優(yōu)化問題(1.1),點列{xk}的迭代格式為

這里的αk為步長.本文選用精確線搜索計算αk,即每步迭代中選擇αk滿足

選取步長因子αk最好的方法就是使目標(biāo)函數(shù)沿著搜索方向dk達(dá)到極小,從理論上來說,精確線搜索所得到的步長因子有著最好的下降量.例如Zoutendijk[1]證明了采取精確線搜索的FR方法對一般非凸函數(shù)總收斂;從文獻(xiàn)[2]中的結(jié)果可知用精確線搜索的PRP方法對一致凸函數(shù)全局收斂;Rivaie[3]提出了一個新算法在精確線搜索下有更好的結(jié)果.

搜索方向dk的迭代格式為

其中g(shù)k=▽f(xk),如果用θk表示向量dk與?gk的夾角,則有

這里的βk為一標(biāo)量,著名的βk公式有(可參看文獻(xiàn)[4–8])

其中‖·‖表示歐式范數(shù).通常情況下,FR和DY方法有很好的收斂性,而PRP和HS方法卻有很好的數(shù)值效果.學(xué)者們?yōu)榱藢ふ壹饶鼙ＷC收斂性又可以有良好數(shù)值效果的算法,在以上公式的基礎(chǔ)上,一方面對βk進(jìn)行改進(jìn)例如文獻(xiàn)[3,9,10],另一方面將不同的βk公式進(jìn)行混合[11–13].最近,文獻(xiàn)[3]中給出了一個新的參數(shù)公式

并得到了該算法在精確線搜索下的全局收斂性.受文獻(xiàn)[12]的啟發(fā),取βNewk為

其中μ為參數(shù)且0＜μ≤1.

2 算法及其性質(zhì)

本文討論一種新的混合共軛梯度法,其中

算法A步驟1給定ε＞0,x1∈Rn,0＜μ≤1,d1=?g1,k:=1.

步驟2若‖gk‖＜ε,則停止;否則轉(zhuǎn)步驟3.

步驟3由精確線搜索計算步長αk,使其滿足(1.3)式.

步驟4令xk+1=xk+αkdk,求gk+1,并用(2.1)式試求βk+1.

步驟5令dk+1=?gk+1+βk+1dk,令k=k+1;轉(zhuǎn)步驟2.

引理2.1對任意k≥1,算法A產(chǎn)生的搜索方向dk滿足,其中C≥0.

證當(dāng)k=1時故結(jié)論成立.

(i)當(dāng)時,若有結(jié)論成立.否則有

因此當(dāng)k＞1時,

因為0＜ μ≤1,故其中C ≥0.

(ii)當(dāng)時,對式(1.3)有

引理2.2同引理2.1中的條件,由式(1.5)和(2.1)可得

證因為

由(2.1)式知,當(dāng)所以

3 全局收斂性

假設(shè)

(H1)目標(biāo)函數(shù)f(x)在水平集L0={x∈Rn|f(x)≤f(x1)}上有下界,其中x1為初始點.

(H2)目標(biāo)函數(shù)f(x)在水平集L0的一個鄰域N 內(nèi)連續(xù)可微,且梯度函數(shù)g(x)滿足Lipschitz連續(xù),即存在常數(shù)L＞0,使

引理3.1若(H1),(H2)成立,考慮一般方法xk+1=xk+αkdk,其中dk滿足步長αk滿足精確線搜索(1.6)式,則有

證由(1.6)式,αk=min{α|?f(xk+αdk)Tdk=0,α ＞ 0},即g(xk+αkdk)Tdk=0.再由 Lipschitz 條件 (3.1),有 ‖g(xk+ αkdk)? g(xk)‖ ·‖dk‖ ≤ Lαk‖dk‖2.由 Cauchy-Schwartz不等式可得

所以即又因為由假設(shè)可知,對一切α＞0都成立

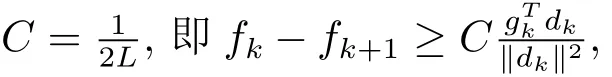
定理3.1設(shè)目標(biāo)函數(shù)滿足假設(shè)(H1),(H2),若存在常數(shù)m ＞0,使得‖g(x)‖≤m,?x∈L0,迭代點列{xk}由算法A產(chǎn)生,則有

證假設(shè)定理不成立,所以存在一個常數(shù)C＞0,有‖g(x)‖≤C.由dk+gk=βkdk?1,對等式兩端取模平方,并移項得到

由引理2.2可知所以

兩邊除以得

又因為

所以

所以

即

與引理3.1中的(3.2)式矛盾,故

證畢.

參考文獻(xiàn)

[1]Zoutendijk G.Nonlinear programming,computational methods[J].Integ.Nonl.Prog.,1970:37–86.

[2]Powell M J D.Restart procedures for the conjugate gradient method[J].Math.Prog.,1977,12(1):241–254.

[3]Rivaie M,Mamat M,June L W,Mohd I.A new class of nonlinear conjugate gradient coefficients with global convergence properties[J].Appl.Math.Comp.,2012,218:11323–11332.

[4]Hestenes M R,Stiefel E L.Methods of conjugate gradients for solving linear systems[J].J.Res.Nat.Bureau Stand.,1952,5(49):409–436.

[5]Fletcher R,Reeves C.Functions minimization by conjugate gradients[J].Comp.J.,1964,7(2):149–154.

[6]Polak E,Ribi′ere G.Note sur la convergence de m′ethodes de directions conjug′ees[J].Rev.Fran.Inform.Rech.Op′erationelle,1969,16(3):35–43.

[7]Polyak B T.The conjugate gradient method in extreme problems[J].USSR Comp.Math.Math.Phys.,1969,9:94–112.

[8]Dai Y H,Yuan Y X.A Nonlinear conjugate gradient method with a strong global convergence property[J].SIAM J.Optim.,1999,10:177–182.

[9]Rivaie M,Mamat M,Abashar A.A new class of nonlinear conjugate gradient coefficients with exact and inexact line searches[J].Appl.Math.Comp.,2015,268:1152–1163.

[10]Xu Z S.A class of new conjugate gradient methods[J].J.Math.,2002,22(1):27–30.

[11]江羨珍,韓麟,簡金寶.Wolfe線搜索下一個全局收斂的混合共軛梯度法[J].計算數(shù)學(xué),2012,34(1):103–112.

[12]戴志峰,陳蘭平.一種混合的HS-DY共軛梯度法[J].計算數(shù)學(xué),2005,27(4):429–436.

[13]景書杰,鄧濤.精確線搜索下具有充分下降性的混合共軛梯度法[J].河南理工大學(xué)學(xué)報(自然科學(xué)版),2010,29(2):266–273.