季海波

(宿遷學院 文理學院, 江蘇 宿遷 223800)

0 引言

k階Erlang分布的隨機變量是k個獨立的同參數(shù)的指數(shù)分布隨機變量的和,它是一種Phase-Type分布,是亞指數(shù)分布的一個特例(各階指數(shù)過程的均值都相等的k階亞指數(shù)分布就是k階Erlang分布),而指數(shù)分布是k階Erlang分布的特例．相比于指數(shù)分布,k階Erlang分布能更好地對現(xiàn)實數(shù)據(jù)進行擬合(更適用于多個串行過程,或者無記憶性假設不顯著的情況下),故在排隊論中被廣泛應用,在保險金融中也被用作索賠分布,在不同損失下對其他分布參數(shù)的研究也不少[1-3],但國內(nèi)對該分布的統(tǒng)計性質進行的研究不多．本文主要研究了在不同損失函數(shù)下k階Erlang分布參數(shù)的Bayes估計．

定義1[4]若X1,X2,…,Xk是一列獨立的隨機變量,且都服從指數(shù)分布E(μ),則隨機變量T=X1+X2+…+Xk具有概率密度

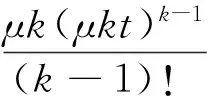
或者等價地,其分布函數(shù)為

稱T服從參數(shù)為μ的k階Erlang分布．

為便于估計,令θ=kμ,則k階Erlang分布的密度函數(shù)和分布函數(shù)分別為

(1)

(2)

其中θ>0．

從k階Erlang分布中抽取容量為n的簡單樣本T1,T2,…,Tn,記T(T1,T2,…,Tn),t(t1,t2,…,tn)為T的觀測值,則樣本t的似然函數(shù)為

(3)

1 不同損失函數(shù)下θ的Bayes 估計

引理1 設T=(T1,T2,…,Tn)是來自分布(1)的一個簡單隨機樣本,若參數(shù)θ的先驗分布取指數(shù)分布E(λ),λ>0,則θ的后驗密度函數(shù)為

(4)

證明設參數(shù)θ的先驗分布為E(λ),λ>0,則

π(θ)=λe-λθ(λ,θ>0),

樣本t=(t1,t2,…,tn)關于θ的條件密度為

則參數(shù)θ的后驗密度函數(shù)為

得證．

而在Bayes估計中,損失函數(shù)的選取將會對參數(shù)估計量的優(yōu)良性有較大影響．下面將取不同的損失函數(shù)來得到參數(shù)θ的Bayes估計．

證明由文[5]及引理1,可得在平方損失函數(shù)L(θ,δ)=(θ-δ)2下

再由文[5],在給定的Bayes決策中,若在給定的先驗分布下,θ的Bayes估計δ0(x)唯一且是容許的．

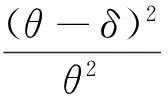
證明由文[3]及引理1,可得在二次損失函數(shù)下

由文[5]知,在給定的Bayes決策中,若在給定的先驗分布下,θ的Bayes估計δ0(x)唯一且是容許的．

證明由文[3]中定理1定理2,可得在平衡損失函數(shù)下

由文[5]知,在給定的Bayes決策中,若在給定的先驗分布下,θ的Bayes估計δ0(x)唯一且是容許的．

定理4 在Linex損失函數(shù)L(θ,δ)=ec(δ-θ)-c(δ-θ)-1,(c∈R,c≠0)下,若參數(shù)θ的先驗分布為E(λ),λ>0,則分布(1)中參數(shù)θ的Bayes估計為

從而

由文[5],在給定的Bayes決策中,若在給定的先驗分布下θ的Bayes估計δ0(x)唯一且是容許的．

證明由文[6]及引理1,可得在熵損失函數(shù)下

由文[5],在給定的Bayes決策中,若在給定的先驗分布下,θ的Bayes估計δ0(x)唯一且是容許的．

證明由文[7]及引理1,可得在對稱熵損失函數(shù)下

由文[5],在給定的Bayes決策中,若在給定的先驗分布下,θ的Bayes估計δ0(x)唯一且是容許的．

2 超參數(shù)λ的估計

對于k階Erlang分布的密度函數(shù)用(1)式,取指數(shù)分布為參數(shù)θ的先驗分布,則其邊緣分布為

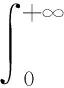
則似然函數(shù)為

令

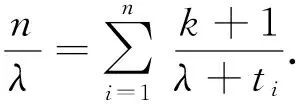
令

且

所以函數(shù)h1(λ)在(0,+∞)是嚴格單調遞減的下凸函數(shù)．

所以函數(shù)h2(λ)在(0,+∞)內(nèi)也是嚴格單調遞減的下凸函數(shù)．

從而方程

在(0,+∞)內(nèi)有唯一解,迭代公式為

(5)

3 Monte Carlo隨機模擬

表1 參數(shù)估計的均值與均方誤差

上述模擬結果表明:

1) 參數(shù)θ的Bayes估計的均方誤差明顯比極大似然估計的均方誤差要小,所以極大似然估計的效果稍差．隨著樣本容量的增大,極大似然估計值越來越靠近真值,而且均方誤差也越來越小,這體現(xiàn)出來了極大似然估計的大樣本優(yōu)越性．

2) 在Linex損失下,參數(shù)c的符號對θ的Bayes估計的差別并不大;從均方誤差看,當樣本容量為30和100時,都是對稱熵損失下的均方誤差最小,而在樣本容量為50時,平方損失下的均方誤差最小;從參數(shù)θ的估計值與真值的接近程度看,平衡損失函數(shù)下θ的估計是最接近的．

因此,由模擬結果所得出的結論可以通過選取的樣本容量的大小來選取不同的估計．當樣本容量不是很大時盡量選取Bayes估計從而提高估計的精度,容量很小或者較大時優(yōu)先考慮對稱熵損失下的Bayes 估計,容量中等時考慮選用平方損失下的Bayes 估計;從估計值與真值的接近程度看,優(yōu)先考慮平衡損失下的Bayes 估計．

[1] 姚惠,謝林.不同損失下Lomax分布形狀參數(shù)的Bayes估計[J].數(shù)學雜志,2011,31(6):1131-1135.

[2] 龍兵.不同損失函數(shù)下艾拉姆咖分布參數(shù)的Bayes 估計——全樣本情形[J].重慶師范大學學報(自然科學版),2013,30(5):96-100.

[3] 孫玉瑩,王德輝.不同損失函數(shù)下偏正態(tài)分布的Bayes估計[J].吉林大學學報(理學版),2012,50(4):638-646.

[4] 胡運權等.運籌學基礎及應用[M].北京:高等教育出版社,1986.

[5] 茆詩松,王靜龍.高等數(shù)理統(tǒng)計[M].北京:高等教育出版社,1998.

[6] 肖小英,任海平.熵損失函數(shù)下兩參數(shù)Lomax分布形狀參數(shù)的Bayes估計[J].數(shù)學的實踐與認識,2010,40(5):227-230.

[7] 周明元. 對稱熵損失函數(shù)下兩參數(shù)Lomax分布形狀參數(shù)的Bayes估計[J].統(tǒng)計與決策,2010(12):161-162.

[8] 茆詩松.貝葉斯統(tǒng)計[M].北京:中國統(tǒng)計出版社,1999.

[9] James O Berger.統(tǒng)計決策論及貝葉斯分析[M].(2版).北京:中國統(tǒng)計出版社,1998.