丁慶紅 肖偉華 馮 夢(mèng)

(1. 北京教育學(xué)院石景山分院,北京 100043; 2. 北京景山學(xué)校遠(yuǎn)洋分校,北京 100040)

·復(fù)習(xí)與考試·

由思維的發(fā)散性到方法的多樣性
——一則運(yùn)動(dòng)學(xué)問(wèn)題的解法欣賞

丁慶紅1肖偉華2馮 夢(mèng)2

(1. 北京教育學(xué)院石景山分院,北京 100043; 2. 北京景山學(xué)校遠(yuǎn)洋分校,北京 100040)

對(duì)于同一個(gè)物理問(wèn)題,由于對(duì)物理概念和規(guī)律的理解不同,采用的方法不同,突破的方式不一樣,解決問(wèn)題的路徑也不一樣．下面的螞蟻出洞問(wèn)題是一個(gè)經(jīng)典問(wèn)題,梳理的解法也很經(jīng)典．雖有的簡(jiǎn)捷,有的較繁雜,有的巧妙,但殊途同歸．從中我們可以體會(huì)到正是由于思維的發(fā)散性導(dǎo)致解決問(wèn)題方法的多樣性,有利于發(fā)展創(chuàng)造性思維;從中我們可以體會(huì)物理學(xué)自洽的內(nèi)在美,感受物理學(xué)的力量,發(fā)展對(duì)科學(xué)的熱愛(ài)．

一只螞蟻從洞口爬出后沿一直線(xiàn)運(yùn)動(dòng),其速度大小與其離開(kāi)洞口的距離成反比,當(dāng)其到達(dá)距洞口為l1的A點(diǎn)時(shí)速度為v1,若B點(diǎn)離洞口的距離為l2(l2>l1),求螞蟻由A運(yùn)動(dòng)到B所需的時(shí)間．

解法1： 微元法.

如圖1,將AB之間的距離等分為N(N→∞)份,則每一份的大小為

圖1

由于N→∞,所以每一份的大小都趨近于0,則螞蟻在每一等份中的運(yùn)動(dòng)都可視為勻速運(yùn)動(dòng)．

下面研究螞蟻在第i份運(yùn)動(dòng)所用的時(shí)間ti．

所以,螞蟻從A爬行到B的總時(shí)間為

當(dāng)N→∞時(shí),有

解法2： 類(lèi)比法1.

將螞蟻的運(yùn)動(dòng)與勻變速運(yùn)動(dòng)進(jìn)行類(lèi)比,問(wèn)題中的t和L分別類(lèi)比為初速為0的勻加速直線(xiàn)運(yùn)動(dòng)中的x和t,而1/k相當(dāng)于加速度a,其類(lèi)比后對(duì)應(yīng)的物理量為

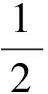
故螞蟻從A運(yùn)動(dòng)到B所需的時(shí)間為

解法3： 積分法.

解法4： 圖像法.

圖2 圖3

解法5： 類(lèi)比法2.

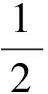
解法6： 中間位置速度法.

將螞蟻從l1的A點(diǎn)爬到距離中心l2的B處這段距離依次分為10小段,取每一小段的中間位置的速度代表該段的平均速度,可以計(jì)算出每一小段的時(shí)間,然后累加,即可得到這種情況下的總時(shí)間．

表1

解法7： 結(jié)論法.

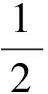
由題意,該段位移中間位置的速度為

可見(jiàn),當(dāng)物體作直線(xiàn)運(yùn)動(dòng)的速度大小與距某點(diǎn)距離的大小成反比時(shí),在這一運(yùn)動(dòng)過(guò)程中,其中間位置的瞬時(shí)速度等于這一運(yùn)動(dòng)過(guò)程中的平均速度．這個(gè)結(jié)論與下面的結(jié)論相對(duì)稱(chēng),當(dāng)物體做勻變速直線(xiàn)運(yùn)動(dòng)時(shí),其中間時(shí)刻的瞬時(shí)速度等于這一運(yùn)動(dòng)過(guò)程中的平均速度．

上面的每一種解法可以說(shuō)都令人拍案叫絕,都令人拍案稱(chēng)奇,有一種“柳暗花明又一村”的感覺(jué)．我們?cè)谛蕾p的同時(shí),可以仔細(xì)體會(huì)物理概念和規(guī)律的魅力,可以感受到物理方法的力量,可以享受到創(chuàng)造性思維帶來(lái)的樂(lè)趣．

2017-08-02)