陳茂源,張立柱

(上海財(cái)經(jīng)大學(xué)數(shù)學(xué)學(xué)院,上海 200433)

Black-Sholes方程的解析解及收斂性分析

陳茂源,張立柱

(上海財(cái)經(jīng)大學(xué)數(shù)學(xué)學(xué)院,上海 200433)

將經(jīng)典的Black-Sholes方程轉(zhuǎn)化為一類特殊的線性偏微分方程,并通過對(duì)其采用Fourier變換方法求得解析解,最后利用優(yōu)核的相關(guān)性質(zhì)對(duì)所得Black-Sholes方程解析解進(jìn)行收斂性分析,證明了該解析解的收斂性.

Black-Sholes方程;Fourier變換;優(yōu)核

1 背景

期權(quán)又稱為選擇權(quán),是一種衍生性金融工具,是指買方向賣方支付期權(quán)費(fèi)后擁有的在未來一段時(shí)間內(nèi)或未來某一特定日期以事先規(guī)定好的價(jià)格向賣方購買或出售一定數(shù)量的特定商品的權(quán)利,但不負(fù)有必須買進(jìn)或賣出的義務(wù).期權(quán)已經(jīng)成為企業(yè)進(jìn)行風(fēng)險(xiǎn)管理的核心工具.對(duì)期權(quán)定價(jià)問題的研究,近年來已有了較為成熟的理論成果.尤其是哈佛大學(xué)的資深教授Robert Merton和斯坦福大學(xué)的榮譽(yù)退休教授Myrn Scholes在1973年提出來的Black-Scholes公式[1],給期權(quán)定價(jià)理論帶來開創(chuàng)性的貢獻(xiàn).在該公式的基礎(chǔ)上,引入各種復(fù)雜參數(shù)的定價(jià)研究發(fā)展迅速[2].除了期權(quán)定價(jià)領(lǐng)域,該公式還適用于其他方面,如公司價(jià)值評(píng)估[3],資源配置中利用該定價(jià)思想,利用電動(dòng)汽車實(shí)現(xiàn)對(duì)電力系統(tǒng)的合理利用[4]等.

Black-Sholes方程把人們引入了一個(gè)風(fēng)險(xiǎn)中性的世界,它的定價(jià)理論不依賴于每個(gè)投資人的偏好以及對(duì)未來風(fēng)險(xiǎn)資產(chǎn)的期望值,因此通過求解Black-Sholes方程所得到的價(jià)格是一個(gè)風(fēng)險(xiǎn)中性價(jià)格.通過隨機(jī)微分方程的推導(dǎo)得原始的Black-Sholes方程：

其中s為股票的現(xiàn)價(jià),V(s,t)是衍生品的價(jià)格,是時(shí)間和股票價(jià)格的函數(shù),r是無風(fēng)險(xiǎn)年利率,σ為波動(dòng)率.方程(1)與傳統(tǒng)的偏微分方程定解問題不同.首先,盡管方程是線性的,但是其系數(shù)不是常系數(shù)的.其次,問題(1)的定解條件并不是給定t=0時(shí)刻的函數(shù)值V(s,0),而是個(gè)定最終時(shí)刻t=T時(shí)刻的函數(shù)值V(s,T),因此是一類倒向偏微分方程定解問題.

Fourier分析方法目前廣泛應(yīng)用于求解偏微分方程定解問題,如對(duì)熱傳導(dǎo)方程,波動(dòng)方程及流體中的相關(guān)方程都有成功求解案例[8,11].許多對(duì)復(fù)雜期權(quán)定價(jià)的研究都可以借助Fourier變換的方法來求解[5-6,9].近幾年對(duì)于美式期權(quán)的研究,由于其復(fù)雜的初始條件,也出現(xiàn)了新的采用同倫分析方法求解的方法[7].

本文首先采用Fourier分析方法求解一類特殊的正向線性偏微分定解問題,其次通過變量代換將經(jīng)典的Black-Sholes方程(1)轉(zhuǎn)換成這類可求解的定解問題,最后借助Fourier變換中的優(yōu)核[10-11]性質(zhì)對(duì)所得解析解進(jìn)行收斂性分析,并證明解析解的收斂性.

2 一類線性偏微分方程的解

考慮如下線性偏微分方程：

注意到u(x,t)在方程中關(guān)于x的偏導(dǎo)數(shù)部分與常微分方程中的Euler方程類似,可以考慮做變換

記

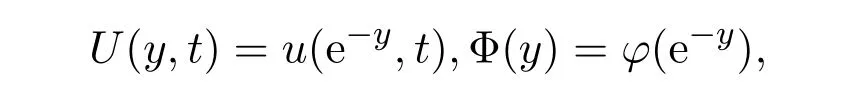
于是

類似地有

將其代入原定解問題(2)中,得到

這是一個(gè)常系數(shù)偏微分方程初值問題,當(dāng)a=1時(shí),問題就是經(jīng)典的熱傳導(dǎo)定解問題.受此啟發(fā),考慮采用Fourier變換法求解.對(duì)方程兩邊做Fourier變換,并記對(duì)U和Φ的Fourier變換為：

得到定解問題(2)的解：

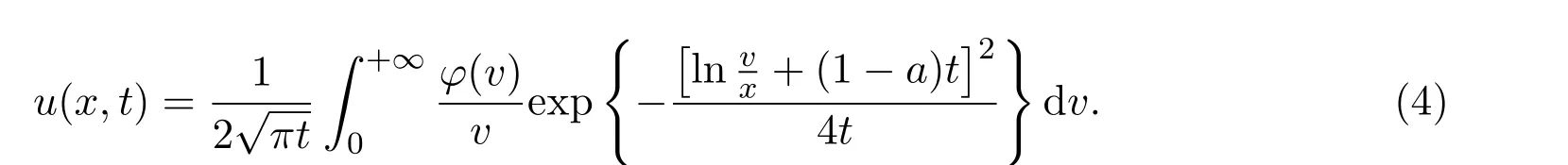
3 解的收斂性分析

在上述求解過程中可看出,定解問題(3)的解實(shí)際上就是利用初始條件與核函數(shù)

做卷積.由文獻(xiàn)[10-11]可知,當(dāng)Kt(y)為實(shí)數(shù)域(t→0)上的優(yōu)核時(shí),得到的解U(y,t)是收斂的,從而定解問題(2)的解(4)也是收斂的.優(yōu)核定義如下：

定義 3.1[10-11]核函數(shù)Kt(x)稱為優(yōu)核,如果Kt(x)滿足如下三個(gè)條件：

1.對(duì)任意的t＞0,有

2.存在 M ＞0,對(duì)任意的t＞0,有

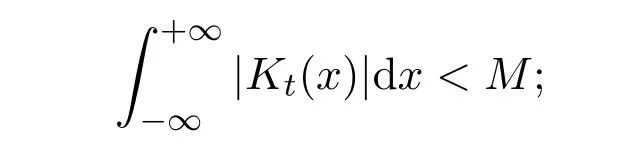
3.對(duì)任意 η＞0,當(dāng)t→0時(shí),有

下面證明Kt(x)滿足優(yōu)核條件

定理3.1核函數(shù)

是優(yōu)核.

證明1.對(duì)于任意的t＞0,有

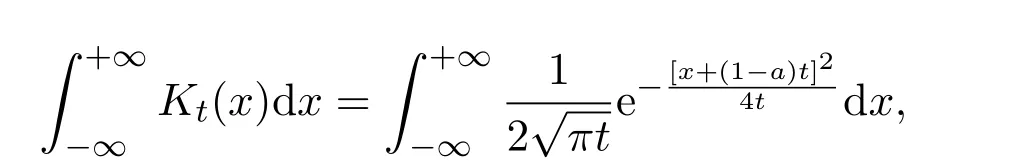
令

可得

即優(yōu)核的條件1滿足.

2.由Kt(x)的表達(dá)式可知,對(duì)任意的x,Kt(x)恒為正,即

從而存在M ＞1,使得對(duì)任意t＞0,都有

即優(yōu)核的條件2滿足.

3.對(duì)任意η＞0,有

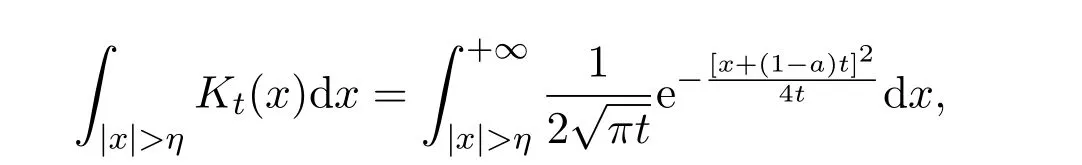
做變換

可得

當(dāng)t→0時(shí),顯然有上式趨于0,即優(yōu)核的條件3滿足.

綜上可知,

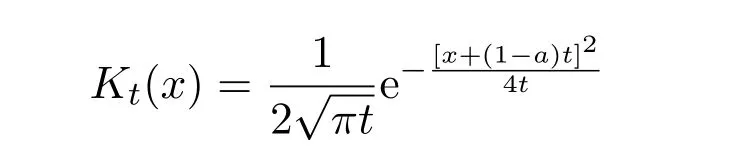
是優(yōu)核.

4 Black-Sholes方程的解析解及收斂性

首先做變換

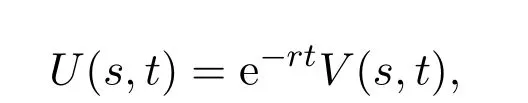
對(duì)方程(1)兩邊同乘e?rt,方程可化為：

為將倒向微分問題化為正向初值問題,再做變換

令

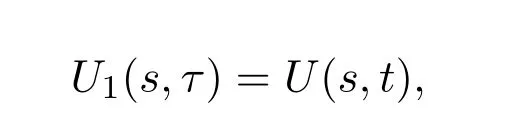
從而將方程(5)化為：

其對(duì)應(yīng)的初值條件為：

定解問題(6)(7)與定解問題(2)形式上完全一致,因此可類似求得問題(6)(7)的解為：

最后,將

回代,并利用

就得到Black-Sholes方程(1)的解析解

最后討論Black-Sholes解析解(9)的收斂性.由以上分析可知,Black-Sholes方程是一類特殊的線性偏微分方程,根據(jù)在第3節(jié)中收斂性分析的結(jié)果,取特殊情況,令

就是Black-Sholes方程的解析解.更具體一點(diǎn)說就是,利用Fourier變換法求解Black-Sholes方程時(shí)所采用的核函數(shù)依舊是

而根據(jù)定理3.1知其是優(yōu)核,從而所得解析解(9)就是收斂的.

5 結(jié)論

本文首先采用傅里葉變換的方法,求解一類非常系數(shù)的線性偏微分方程定解問題.之后將經(jīng)典的Black-Sholes方程轉(zhuǎn)化為這類可求解的線性偏微分方程,從而得到其解析解.最后利用優(yōu)核性質(zhì)對(duì)所得解析解進(jìn)行收斂性分析,證明了所得解析解是收斂的.

參考文獻(xiàn)

[1]Black F,Sholes M.The pricing options and corporate liabilities[J].Journal of Political Economy,1973,81：637-659.

[2]姜禮尚.期權(quán)定價(jià)的數(shù)學(xué)模型和方法[M].2版.北京：高等教育出版社,2008．

[3]鄭常德.布萊克─肖爾斯期權(quán)定價(jià)模型在公司價(jià)值評(píng)估中的應(yīng)用[J].中國管理科學(xué),1997,7(1)：1-6.

[4]黃守軍,楊俊,陳其安.基于 B-S期權(quán)定價(jià)模型的 V2G備用合約協(xié)調(diào)機(jī)制研究 [J].中國管理科學(xué),2016,24(10)：10-21

[5]Scott,Louis.Pricing stock options in a jump-di ff usion model with stochastic volatility and interest rates：application of Fourier inversion methods[J].Mathematical Finance,1997,7：413-426.

[6]Bakshi,Gurdip,Chen Zhiwu.An alternative valuation model for contingent claims[J].Journal of Financial Economics,1997,44(1)：123-165.

[7]Heston,Steven.A closed-form solution for options with stochastic volatility with applications to bond and currency options[J].Review of Financial Studies,1993,6：327-343.

[8]Zhang L Z,Tang H S,Maa J P Y,et al.Exact solutions and analysis for a class of extended Stokes′problems[J].Discontinuity Nonlinearity and Complexity,2013,2(1)：85-102.

[9]Cheng Jun,Zhu Songping,Liao Shijun.An explicit series approximation to the optimal exercise boundary of American put options[J].Communications in Nonlinear Science and Numerical Simulation,2010,15：1148-1158.

[10]王志珍.Fourier分析中的幾個(gè)核函數(shù)研究[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2015,31(3)：238-244.

[11]Stein E M,Shakarchi R.Fourier Analysis,an Introduction[M].Princeton：Princeton Univ.Press,2011.

Analytical solution and convergence analysis of Black-Sholes equation

Chen Maoyuan,Zhang Lizhu
(School of Mathematics,Shanghai University of Finance&Economics,Shanghai200433,China)

In this paper,the classical Black-Sholes equation is translated into a special class of linear partial di ff erential equations whose analytic solutions can be found by using Fourier transform method.Furthermore,the convergence of the analytical solution is discussed by using the properties of good kernel.The analytical solution is proved to be convergent.

Black-Sholes equation,Fourier transform,good kernel

O29

A

1008-5513(2017)04-0352-07

10.3969/j.issn.1008-5513.2017.04.003

2017-05-03.

國家自然科學(xué)基金(11201284).

陳茂源(1994-),碩士研究生,研究方向：Fourier分析.

2010 MSC:35K08