(School of Mathematics and Statistics ,Hainan Normal University, Haikou 571158, China)

1 Introduction

Suppose thatX1,…,Xnare nonnegative independent and identically distributed random variables with density functiong(x), whereg(x) is determined by underlying densityf(x) such that

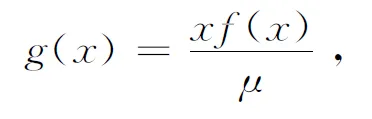
(1.1)

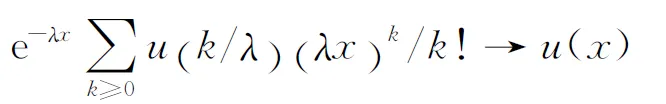
Survival analysis is a branch of statistics. In engineering, economics or sociology, it is referred as to reliability theory. In survival analysis, the MRL function

m(x)=EfX-xX>x

(1.2)

also has some important applications[1]. In some situations, it is more useful than hazard function[2]. The standard nonparametric estimator of MRL function is based on the kernel density estimator. Since the kernel density has a fallacy of boundary issue, which is partially caused by symmetric kernels, the kernel method might not be proper to be applied to estimate the MRL function using length- biased data. Inspired by Hille’s lemma 1.1, we will proposed a smooth MRL function estimator with Poisson weights.

The paper is organized as the following. In section 2, we will present the smooth estimator and investigate its asymptotic properties. Some demonstration examples and conclusions are given in the section 3.

2 Smooth Estimator of Mean Residual Life Function

In this section, we propose a smooth estimator of MRL function and investigate its asymptotic properties, one being its strong consistency and the other being its asymptotic normality.

If we define

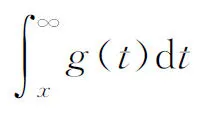
(2.3)

and

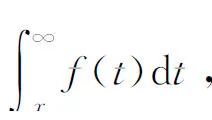
(2.4)

then the mean residual life function is given by

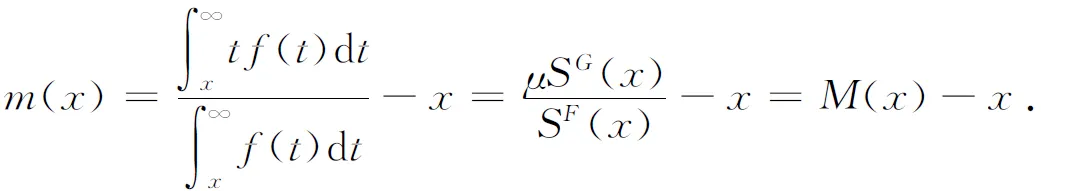
(2.5)

The empirical estimators ofSG(x) andSF(x)/μare given by, respectively,

and

Using Hille’s lemma, we can obtain the following two smooth estimators

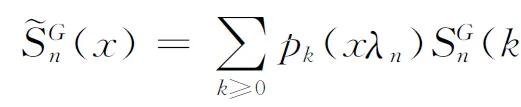
(2.6)

and

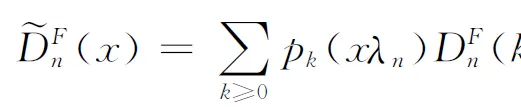
(2.7)

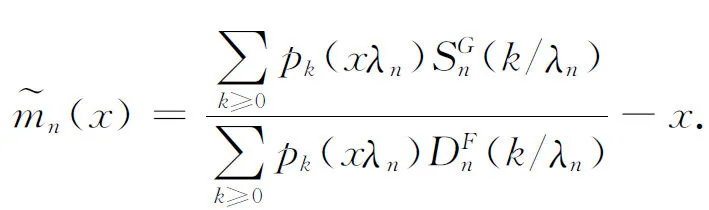
(2.8)

The strong consistency and asymptotic normality of are given by the following two theorems. First of all, we consider the strong consistency.

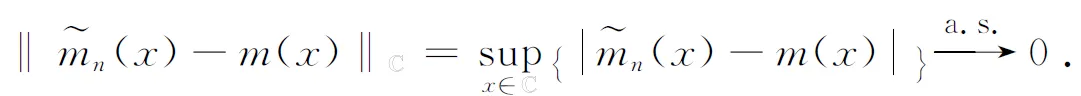
ProofThe proof is straightforward. According to Hille’s lemma, asλn↑∞, we have

(2.9)

and

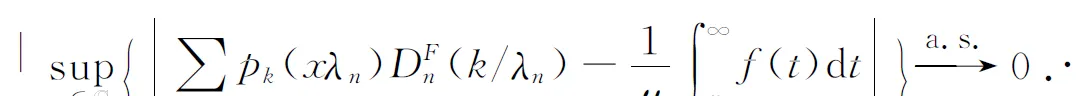
(2.10)

By (2.9) and (2.10), we have

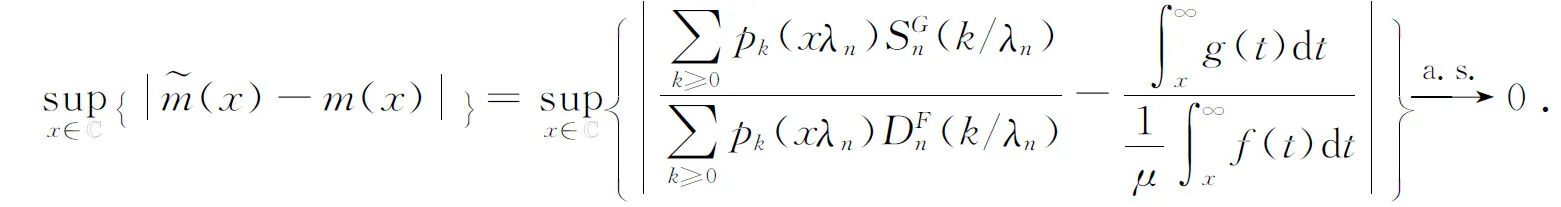
(2.11)

The asymptotic normality is given by the following theorem.

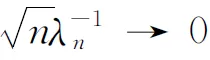
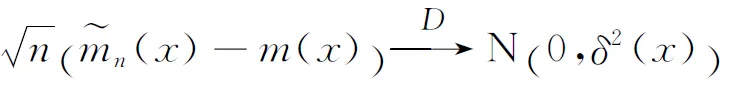
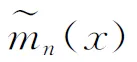
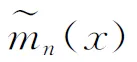
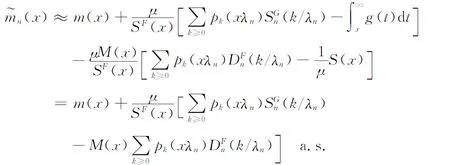
(2.12)

Actually, we can write

(2.13)

and

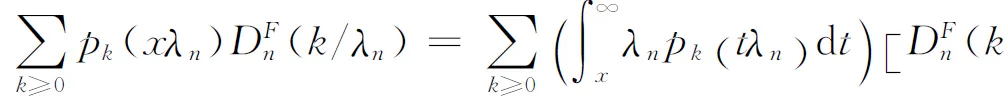
(2.14)

Let

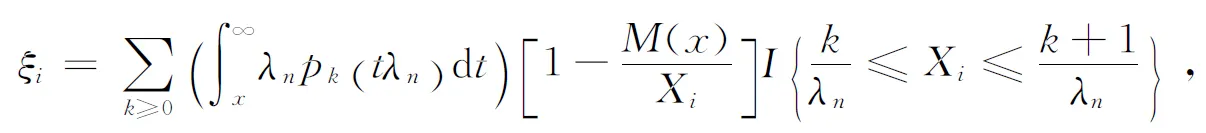
(2.15)

then

(2.16)

So, by (2.12), we have

ξi→m(x).

(2.17)

On the other hand, we have

(2.18)

then

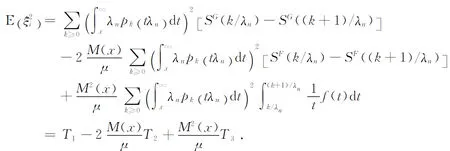
(2.19)

Furthermore

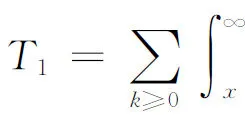
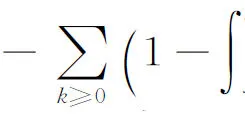
=S1-S2.

(2.20)

Calculating the integration inS1and rearranging the sum give us

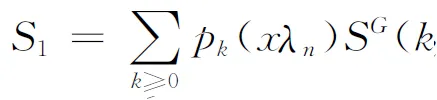
(2.21)

By Hiller’s lemma, we can claim that, asλn↑∞,

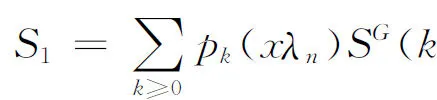
(2.22)

Next, we will show thatS2→ 0.

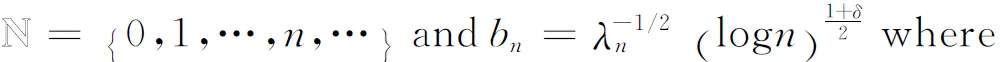
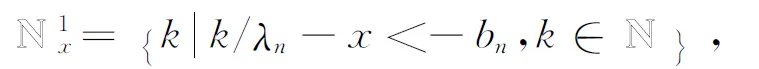
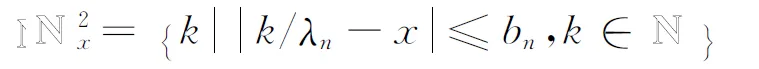
and

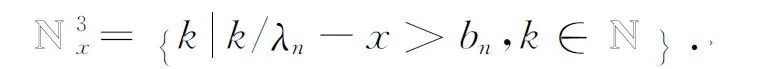
Let

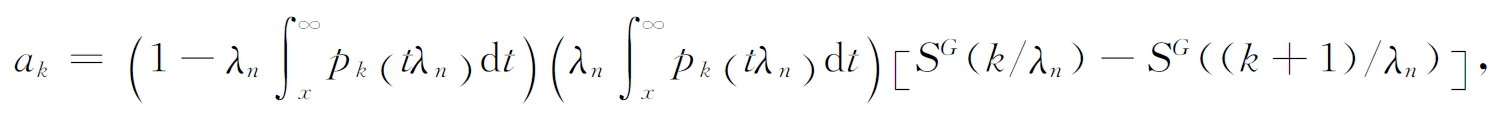
(2.23)

then we can write

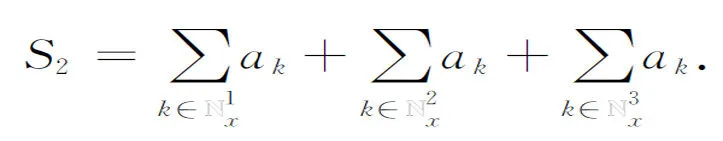
(2.24)

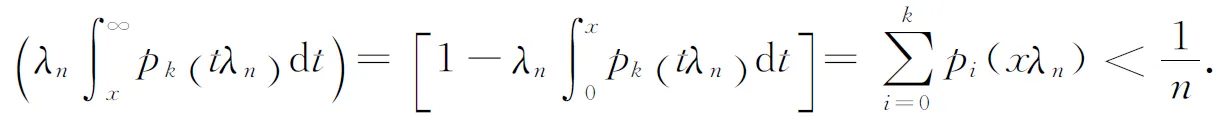
Then

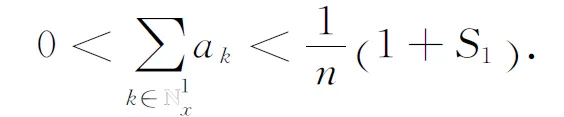
(2.25)

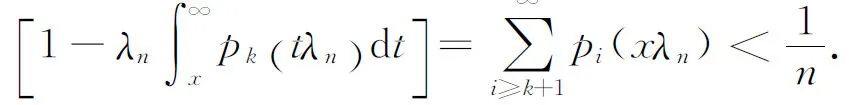
At the same time, we have

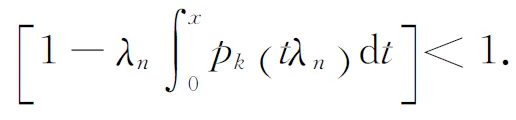
Then

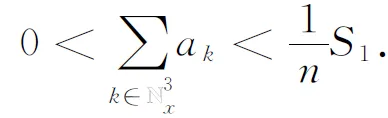
(2.26)

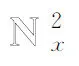
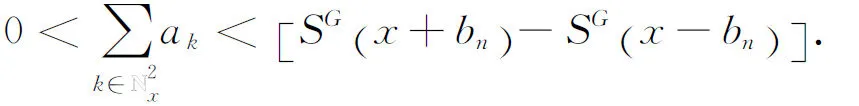
(2.27)

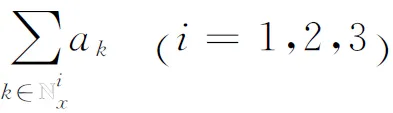
S2→0.

(2.28)

By (2.22) and (2.28), we have

T1→SG(x).

(2.29)

Similarly, we have

T2→F(x)

(2.30)

and

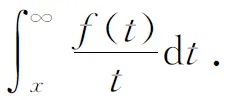
(2.31)

By (2.16), (2.19), (2.29),(2.30) and (2.31) and a little work of algebra, we have

Vξi→δ2(x).

(2.32)

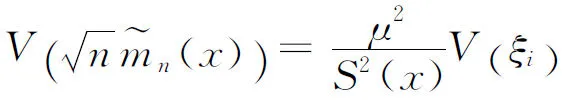
3 Demonstration Examples

In this section, we demonstrate some examples based on weibull distribution, which is usually used as parametric model in survival analysis and whose underlying density is given by

f(x)=αxα-1e-xαI{x>0}.

The generation of length-biased data for weibull distribution is that, first we generate samplesYs with gamma distribution which has a density

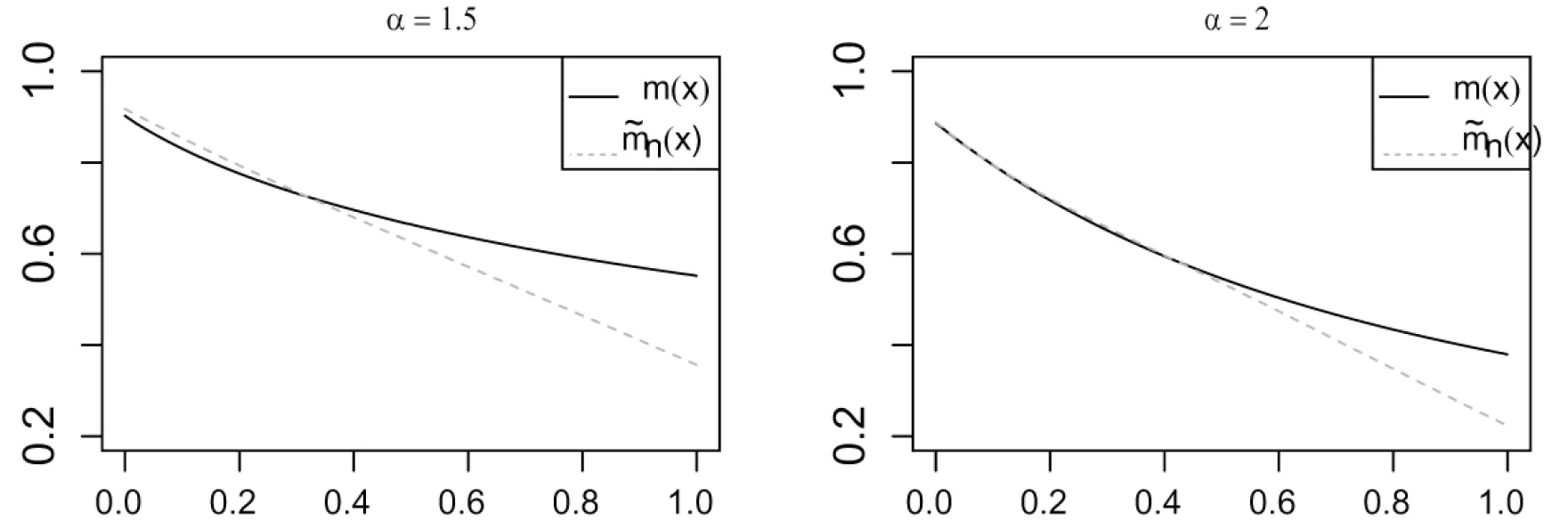
Figure 1 Plots of MRL function and its smooth estimator

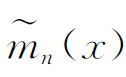
[References]：

[1] Abdous B and Berred A. Mean residual life estimation[J]. Journal of Statistical Planning and Inference, 2005,132:3-19.

[2] Calabria R and Pulcini G. On the asymptotic behaviour of mean residual life function[J]. Reliability Engineering,1987, 19:165-170.

[3] Chaubey Y P and Sen P K. On smooth estimation of survival and density function[J]. Statistics and Decision,1996, 14:1-22.

[4] Chaubey Y P, Sen P K and Li J. Smooth Density Estimation for Length Biased Data[J]. Journal of the Indian Society of Agricultural Statistics, 2010, 64(2):145-155.

[5] Cox D R. Some Sampling Problems in Technology in New Developments in Survey Sampling[M]. N.L. Johnson and H. Smith. New York: John Wiley, 1969:506-527.

[6] Rao C R. On Discrete Distributions Arising out of Methods of Ascertainment[M]. Patil G P. In Classical and Contagious Discrete Distribution. Pergamon Press and Statistical Publishing Society, Calcutta, 1965: 320-332.